Chuyên đề Toán 11 Cánh diều Chuyên đề 2. Làm quen với một vài yếu tố của lí thuyết đồ thị
Chuyên đề Toán 11 Cánh diều Chuyên đề 2. Làm quen với một vài yếu tố của lí thuyết đồ thị
-
1720 lượt thi
-
24 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
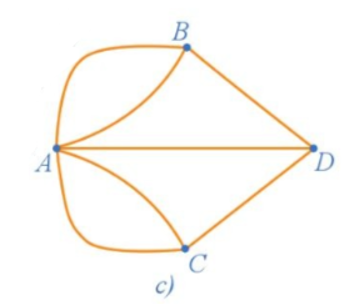
17/07/2024Đọc tên các đỉnh, các cạnh của đồ thị ở Hình 2c.
 Xem đáp án
Xem đáp án
Ở đồ thị Hình 2c có:
+ Các đỉnh là: A, B, C, D.
+ Các cạnh là: AB, AC, AD, BA, BD, CA, CD.
Câu 2:
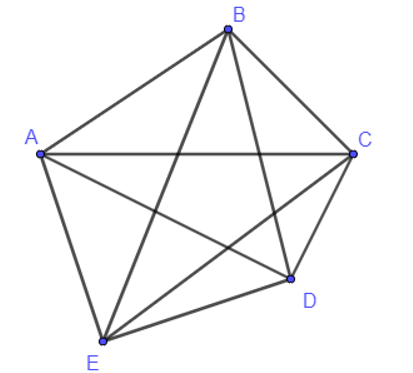
22/07/2024Có năm thành phố A, B, C, D, E sao cho hai thành phố bất kì trong chúng đều có đúng một đường nối với nhau. Sử dụng đồ thị để mô tả tình huống đó.
 Xem đáp án
Xem đáp án
Sử dụng điểm để biểu diễn vị trí thành phố, đoạn thẳng biểu diễn đường đi giữa hai thành phố, ta có mô hình như hình dưới đây.
Câu 3:
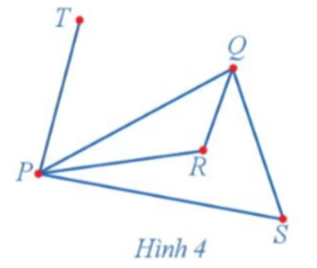
18/07/2024Quan sát đồ thị ở Hình 4 và cho biết:
a) Với mỗi cặp đỉnh của đồ thị, có nhiều nhất bao nhiêu cạnh nối chúng;
b) Có hay không một đỉnh được nối với chính nó bởi một cạnh của đồ thị.
 Xem đáp án
Xem đáp án
Quan sát đồ thị Hình 4 ta thấy:
a) Với mỗi cặp đỉnh của đồ thị, có nhiều nhất một cạnh nối chúng.
b) Không có đỉnh nào được nối với chính nó bởi một cạnh của đồ thị.
Câu 5:
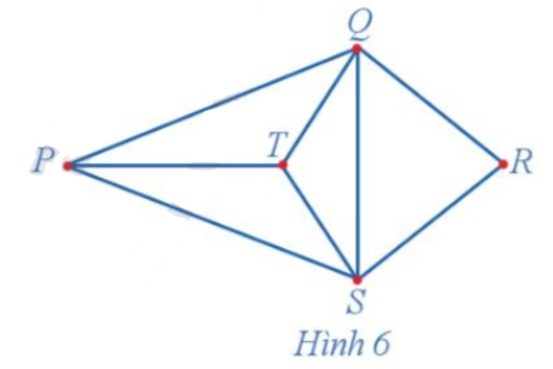
18/07/2024Quan sát đồ thị ở Hình 6 và đếm số cạnh của đồ thị nhận đỉnh P làm đầu mút.
 Xem đáp án
Xem đáp án
Các cạnh của đồ thị nhận đỉnh P làm đầu mút là PQ, PT, PS. Vậy có 3 cạnh của đồ thị nhận đỉnh P làm đầu mút.
Câu 6:
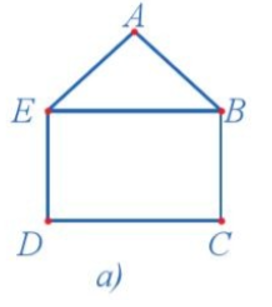
19/07/2024Có bao nhiêu đỉnh bậc lẻ trong đồ thị ở Hình 5a?
 Xem đáp án
Xem đáp án
Quan sát Hình 5a ta thấy d(A) = 2, d(B) = 3, d(C) = 2, d(D) = 2 và d(E) = 3 nên B, E là các đỉnh bậc lẻ. Vậy có hai đỉnh bậc lẻ trong đồ thị ở Hình 5a.
Câu 7:
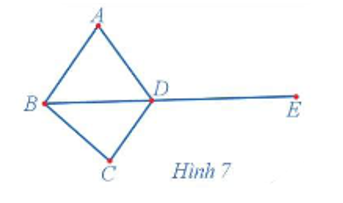
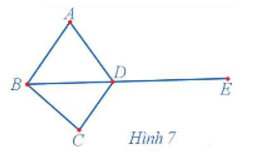
23/07/2024Quan sát đồ thị Hình 7 và cho biết:
a) Tổng các bậc của năm đỉnh trong đồ thị đó;
b) Số cạnh của đồ thị đó;
c) Tổng các bậc của năm đỉnh trong đồ thị gấp bao nhiêu lần số cạnh của đồ thị đó.
 Xem đáp án
Xem đáp án
Quan sát đồ thị Hình 7 ta thấy:
a) d(A) = 2, d(B) = 3, d(C) = 2, d(D) = 4, d(E) = 1.
Do đó, tổng các bậc của năm đỉnh trong đồ thị đó là 2 + 3 + 2 + 4 + 1 = 12.
b) Số cạnh của đồ thị đó là 6.
c) Ta có: 6 . 2 = 12 nên tổng các bậc của năm đỉnh trong đồ thị gấp hai lần số cạnh của đồ thị đó.
Câu 8:
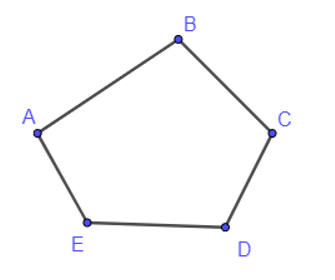
19/07/2024Cho ví dụ về một đồ thị có số lẻ đỉnh bậc chẵn.
 Xem đáp án
Xem đáp án
Đồ thị trên có 5 đỉnh A, B, C, D, E với d(A) = d(B) = d(C) = d(D) = d(E) = 2.
Câu 9:
22/07/2024Quan sát đồ thị Hình 7 và cho biết:
a) Hai đỉnh A, B có được nối với nhau bằng một cạnh hay không;
b) Dãy các cạnh kế tiếp nhau AB, BC, CD, DE có đặc điểm gì.
 Xem đáp án
Xem đáp án
Quan sát đồ thị Hình 7 ta thấy:
a) Hai đỉnh A, B có được nối với nhau bằng một cạnh của đồ thị.
b) Dãy các cạnh kế tiếp nhau AB, BC, CD, DE có những tính chất sau: không có cạnh nào xuất hiện hai lần, đỉnh cuối của cạnh bất kì là đỉnh đầu của cạnh tiếp theo và không có đỉnh nào được đi qua hai lần. Dãy các cạnh kế tiếp nhau AB, BC, CD, DE được gọi là một đường đi từ đỉnh A đến đỉnh E.
Câu 10:
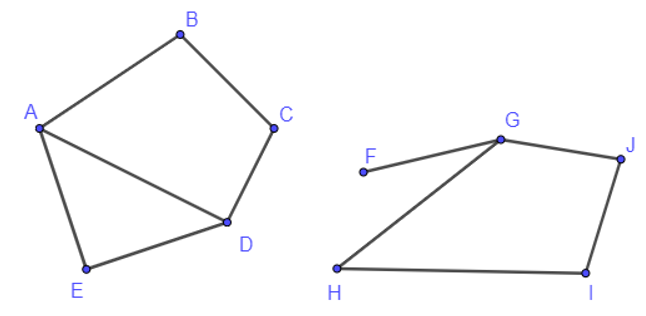
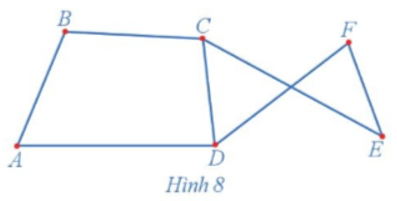
23/07/2024Trong đồ thị ở Hình 8, hãy tìm:
a) Một đường đi từ đỉnh A đến đỉnh F;
b) Một chu trình có đỉnh E là đỉnh đầu và đỉnh cuối.
 Xem đáp án
Xem đáp án
a) Một đường đi từ đỉnh A đến đỉnh F là ADE (hoặc có thể chọn ABCDF hoặc ABCEF).
b) Một chu trình có đỉnh E là đỉnh đầu và đỉnh cuối là ECDFE (hoặc có thể chọn EFDCE).
Câu 11:
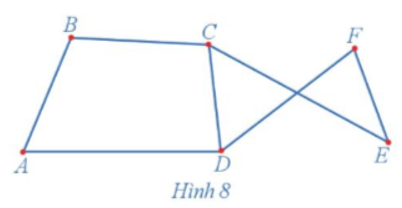
09/07/2024Quan sát đồ thị Hình 8 và cho biết hai đỉnh bất kì của đồ thị có được nối với nhau bằng một đường đi hay không?
 Xem đáp án
Xem đáp án
Quan sát đồ thị Hình 8 ta thấy hai đỉnh bất kì của đồ thị đều được nối với nhau bằng một đường đi.
Câu 12:
22/07/2024Cho ví dụ về một đồ thị liên thông và một đồ thị không liên thông.
 Xem đáp án
Xem đáp án
+) Ví dụ về đồ thị liên thông:
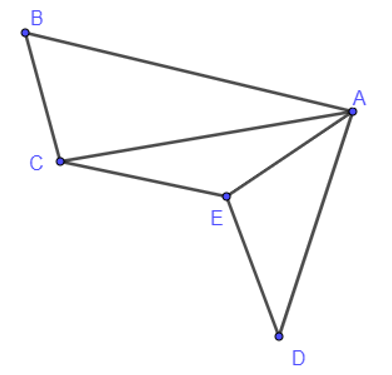
Ở hình trên, hai đỉnh bất kì của đồ thị đều được nối với nhau bằng một đường đi. Vậy đồ thị đó là đồ thị liên thông.
+) Ví dụ về đồ thị không liên thông:
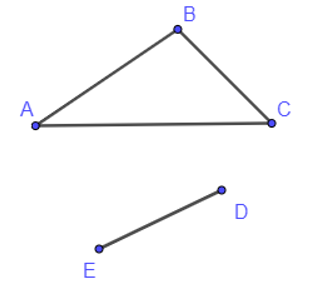
Ở hình trên, mỗi đỉnh thuộc khối bên trên đều không thể nối được với mỗi đỉnh thuộc khối bên dưới bằng một đường đi. Vậy đồ thị đó là đồ thị không liên thông.
Câu 13:
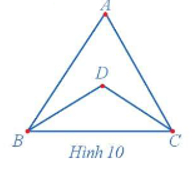
10/07/2024Quan sát đồ thị ở Hình 10 và đường đi CABDCB, cho biết:
a) Đường đi trên có đi qua tất cả các cạnh của đồ thị hay không?
b) Đường đi trên đi qua mỗi cạnh bao nhiêu lần?
 Xem đáp án
Xem đáp án
Quan sát đồ thị ở Hình 10 ta thấy:
a) Đường đi CABDCB đi qua tất cả các cạnh của đồ thị.
b) Đường đi trên đi qua mỗi cạnh đúng một lần.
Câu 14:
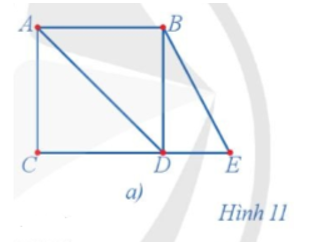
17/07/2024Hãy chỉ ra hai đường đi Euler trong đồ thị ở Hình 11a.
 Xem đáp án
Xem đáp án
Hình 11a có đường đi Euler BEDBADCA và đường đi Euler BEDCADBA.
Câu 15:
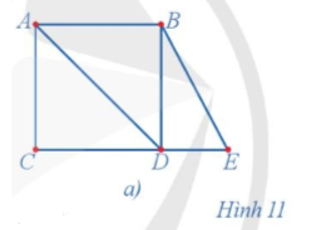
20/07/2024Chứng minh rằng đồ thị ở Hình 11a không có chu trình Euler.
 Xem đáp án
Xem đáp án
Ta có d(A) = 3, d(B) = 3 nên đồ thị ở Hình 11a có đỉnh bậc lẻ, do đó theo định lí Euler, đồ thị ở Hình 11a không có chu trình Euler.
Câu 16:
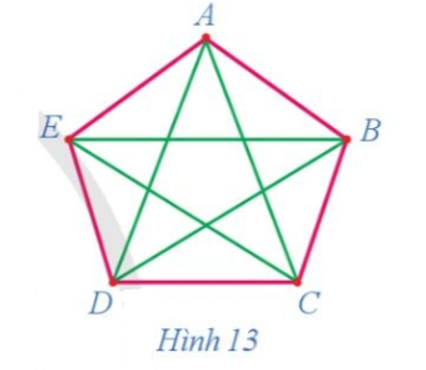
15/07/2024Quan sát đường đi màu đỏ trên đồ thị ở Hình 13 và cho biết đường đi đó có đi qua tất cả các đỉnh của đồ thị hay không và mỗi đỉnh đi qua bao nhiêu lần.
 Xem đáp án
Xem đáp án
Quan sát đường đi màu đỏ trên đồ thị ở Hình 13 ta thấy đường đi đó đi qua tất cả các đỉnh của đồ thị hay và mỗi đỉnh đi qua đúng một lần.
Câu 17:
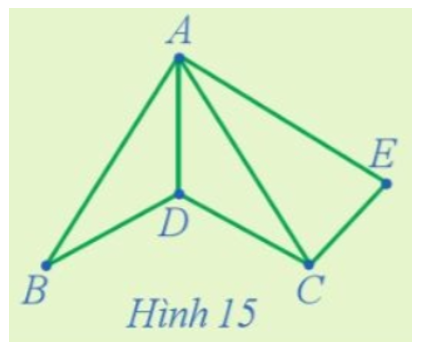
21/07/2024Tìm hai đường đi Hamilton bắt đầu từ đỉnh E của đồ thị trong Hình 15
 Xem đáp án
Xem đáp án
Quan sát đồ thị Hình 15, ta thấy rằng hai đường đi Hamilton bắt đầu từ đỉnh E của đồ thị này là EACDB và ECDBA.
Câu 18:
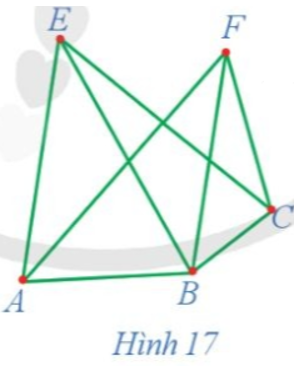
19/07/2024Chứng minh rằng đồ thị G ở Hình 17 có ít nhất một chu trình Hamilton.
 Xem đáp án
Xem đáp án
Ta có: d(A) = 3, d(B) = 4, d(C) = 3, d(E) = 3, d(F) = 3. Đồ thị G ở Hình 17 gồm 5 đỉnh, mỗi đỉnh của đồ thị đều có bậc không nhỏ hơn . Do đó, theo định lí Dirac, đồ thị G có ít nhất một chu trình Hamilton.
Câu 19:
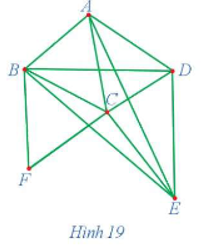
15/07/2024Chứng minh rằng đồ thị G ở Hình 19 có ít nhất một chu trình Hamilton.
 Xem đáp án
Xem đáp án
Đồ thị G ở Hình 19 gồm 6 đỉnh, trong đó các đỉnh A, D, E có bậc 4, các đỉnh B, C có bậc 5 và đỉnh F có bậc 2 nên tổng bậc của hai đỉnh không kề nhau bất kì đều không nhỏ hơn 6. Do đó, theo định lí Ore, đồ thị G có ít nhất một chu trình Hamilton.
Câu 20:
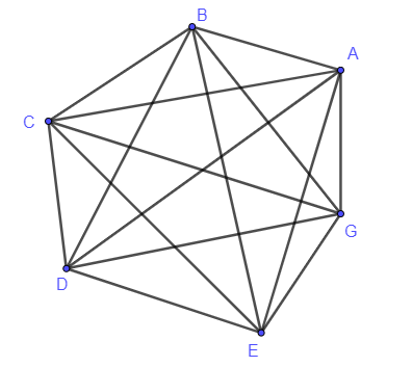
22/07/2024Có sáu thành phố A, B, C, D, E, G sao cho hai thành phố bất kì trong chúng đều có đường nối với nhau. Sử dụng đồ thị để mô tả tình huống đó.
 Xem đáp án
Xem đáp án
Sử dụng điểm để biểu diễn vị trí thành phố, đoạn thẳng biểu diễn đường đi giữa hai thành phố, ta có mô hình như hình dưới đây.
Câu 21:
10/07/2024Hãy vẽ một đồ thị có bốn đỉnh sao cho chỉ có đúng:
a) Hai đỉnh cùng có bậc là 1;
b) Hai đỉnh cùng có bậc là 2.
 Xem đáp án
Xem đáp án
a) Đồ thị chỉ có bốn đỉnh và chỉ có đúng hai đỉnh cùng có bậc là 1 (đỉnh A, đỉnh D).
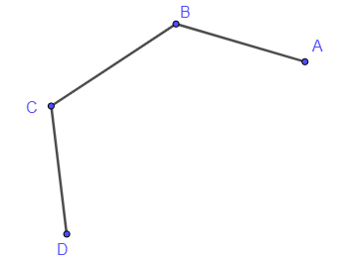
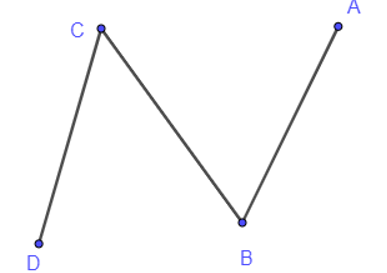
b) Đồ thị chỉ có bốn đỉnh và chỉ có đúng hai đỉnh cùng có bậc là 2 (đỉnh B, đỉnh C).
Câu 22:
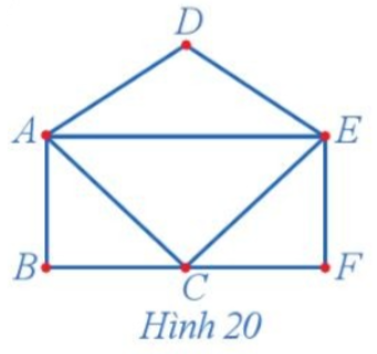
17/07/2024Tìm bậc của mỗi đỉnh và chỉ ra một chu trình Euler (nếu có) của đồ thị ở Hình 20.
 Xem đáp án
Xem đáp án
Ta có: d(A) = 4, d(B) = 2, d(C) = 4, d(D) = 2, d(E) = 4, d(F) = 2.
Vì đồ thị Hình 20 liên thông và không có đỉnh bậc lẻ nên theo định lí Euler thì đồ thị này có chu trình Euler.
Một chu trình Euler của đồ thị ở Hình 20 là AECFEDACBA.
Câu 23:
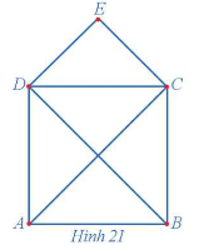
22/07/2024Tìm bậc của mỗi đỉnh và chỉ ra một chu trình Hamilton (nếu có) của đồ thị ở Hình 21.
 Xem đáp án
Xem đáp án
Ta có: d(A) = 3, d(B) = 3, d(C) = 4, d(D) = 4, d(E) = 2.
Vì đồ thị ở Hình 21 gồm có 5 đỉnh nên tổng bậc của hai đỉnh không kề nhau bất kì đều không nhỏ hơn 5. Do đó, theo định lí Ore, đồ thị này có ít nhất một chu trình Hamilton.
Một chu trình Hamilton của đồ thị này là ABCEDA.
Câu 24:
19/07/2024Một cuộc họp có 6 người tham dự. Hai người bất kì trong họ hoặc quen nhau hoặc không quen nhau. Chứng minh rằng có 3 người trong 6 người đó đôi một quen nhau hoặc đôi một không quen nhau.
 Xem đáp án
Xem đáp án
Gọi 6 người bất kì là A, B, C, D, E, G.
Trong 6 người đó ta chọn ra một người A.Trong 5 người còn lại ta chia thành 2 nhóm:
- Nhóm 1 gồm những người quen A.
- Nhóm 2 gồm những người không quen A.
Có 5 người mà chỉ có 2 nhóm. Do đó, tồn tại ít nhất 3 người thuộc cùng một nhóm. Tức là tồn tại ít nhất 3 người quen A hoặc tồn tại ít nhất 3 người không quen A.
- Nếu tồn tại ít nhất 3 người quen A. Gọi 3 người đó là B, C, D:
+ Nếu trong 3 người B, C, D có 2 người nào đó quen nhau. Giả sử 2 người đó là B và C thì ta có 3 người A, B, C là 3 người đôi một quen nhau.
+ Nếu trong 3 người B, C, D không có 2 người nào đó quen nhau thì 3 người B, C, D là 3 người đôi một không quen nhau.
- Nếu tồn tại 3 người không quen A. Giả sử 3 người đó là D, E, G:
+ Trong 3 người D, E, G nếu có 2 người nào đó không quen nhau. Giả sử 2 người đó là D và E thì 3 người A, D, E là 3 người đôi một không quen nhau.
+ Nếu trong 3 người D, E, G không có 2 người nào không quen nhau thì 3 người D, E, G là 3 người đôi một quen nhau.
Vậy trong 6 người bất kì luôn tồn tại 3 người đôi một quen nhau hoặc 3 người đôi một không quen nhau (đpcm).