Nội dung bài viết

    Xem thêm

    Cho đường tròn tâm O có bán kính OA = R, dây BC vuông góc với OA

    Với giải bài 25 trang 112 sgk Toán lớp 9 Tập 1 được biên soạn lời giải chi tiết sẽ giúp học sinh biết cách làm bài tập môn Toán 9. Mời các bạn đón xem:

    1 2,056 04/04/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 9 Luyện tập trang  111, 112

    Video Giải Bài 25 trang 112 Toán lớp 9 tập 1

    Bài 25 trang 112 Toán lớp 9 tập 1: Cho đường tròn tâm O có bán kính OA = R, dây BC vuông góc với OA tại trung điểm M của OA.

    a) Tứ giác OCAB là hình gì ? Vì sao ?

    b) Kẻ tiếp tuyến với đường tròn tại B, nó cắt đường thẳng OA tại E. Tính độ dài BE theo R.

    Lời giải:

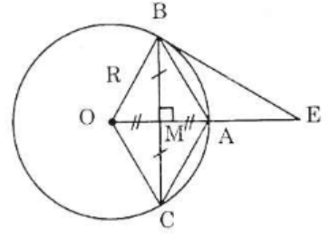
    Tài liệu VietJack

    a)

    Xét đường tròn (O) có

    OA là 1 phần của đường kính và BC là dây của đường tròn mà OA⊥BC tại M

    Do đó, M là trung điểm của BC

     ⇒MB=MC

    Theo đề bài, M là trung điểm của OA 

    ⇒MA=MO

    Xét tứ giác ABOC có:

    OA∩BC tại M

    MB = MC

    MA = MO

    Do đó, tứ giác ABOC là hình bình hành

    Xét hình bình hành ABOC có:

    BC⊥OA tại M

    Do đó, tứ giác ABOC là hình thoi

    b)

    Do ABOC là hình thoi nên BA = BO

    Ta lại có BO = OA = R

    ⇒ OB = OA = BA

    Xét tam giác ABO có: OB = OA = BA (chứng minh trên)

    Do đó, tam giác ABO là tam giác đều.

    ⇒BOA^=60o

    Ta có EB là tiếp tuyến của (O) tại B 

    ⇒EB⊥BO⇒EBO^=90o

    Xét tam giác BOE vuông tại B (do EBO^=90o)

    Áp dụng hệ thức giữa cạnh và góc trong tam giác vuông ta có:

    BE=BO.tanBOE^=R.tan60o=R3

    Xem thêm lời giải bài tập Toán lớp 9 hay, chi tiết khác:

    Bài 24 trang 111 Toán 9 Tập 1: Cho đường tròn (O), dây AB khác đường kính...

    Tham khảo các loạt bài Toán 9 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 2,056 04/04/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: