Câu hỏi:
05/11/2024 718
Vẽ đồ thị của các hàm số sau:
a) y = 2x – 6;
b) y = –3x + 5;
c) .
Vẽ đồ thị của các hàm số sau:
a) y = 2x – 6;
b) y = –3x + 5;
c) .
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
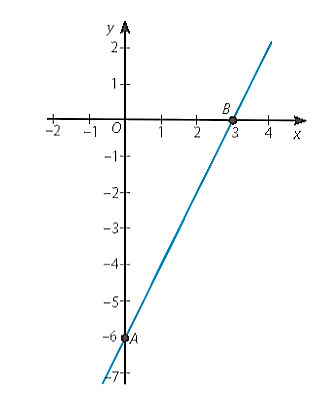
a) y = 2x – 6
Lời giải:
Cho x = 0 thì y = – 6, ta được giao điểm của đồ thị với trục Oy là A(0; – 6).
Cho y = 0 thì x = 3, ta được giao điểm của đồ thị với trục Ox là B(3; 0).
Đồ thị của hàm số y = 2x – 6 là đường thẳng AB.
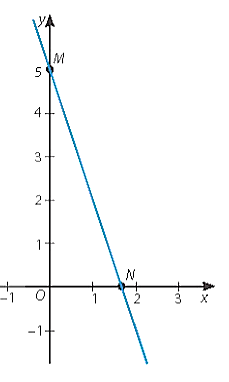
b) y = –3x + 5
Lời giải:
Cho x = 0 thì y = 5, ta được giao điểm của đồ thị với trục Oy là M(0; 5).
Cho y = 0 thì x = , ta được giao điểm của đồ thị với trục Ox là N .
Đồ thị của hàm số y = –3x + 5 là đường thẳng MN.
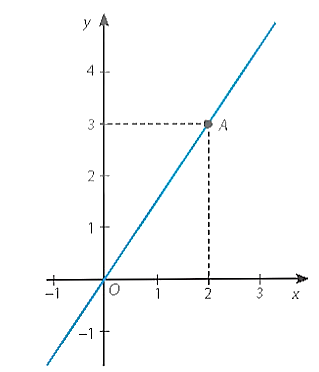
c)
Lời giải:
Cho x = 0 thì y = 0, ta có đồ thị hàm số đi qua gốc tọa độ O(0; 0).
Cho x = 2 thì y = 3, ta có đồ thị hàm số đi qua điểm A(2; 3).
Đồ thị của hàm số là đường thẳng OA.
*Phương pháp giải:
Bước 1: Tìm tập xác định của hàm số.
Bước 2: Lập bảng giá trị (thường từ 3 đến 4 giá trị) tương ứng giữa x và y sao cho các điểm tương ứng nằm bên phải trục Oy.
Bước 3: Vẽ trục tọa độ Oxy và đánh dấu điểm O, các điểm đã lập trong bảng giá trị và các điểm đối xứng với chúng qua trục Oy.
Bước 4: Đồ thị hàm số y = a (a ≠ 0) luôn đi qua gốc tọa độ O và nhận trục Oy làm trục đối xứng. Vẽ đường cong parabol đi qua các điểm đã đánh dấu ta được đồ thị hàm số y = a (a ≠ 0) và kết luận.
*Lý thuyết:
- Đồ thị của hàm số: Đồ thị của hàm số y = a (a ≠ 0) là một parabol đi qua gốc tọa độ O, nhận Oy làm trục đối xứng (O là đỉnh của parabol)
+) Nếu a > 0 thì đồ thị nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị.
+) Nếu a < 0 thì đồ thị nằm phía dưới trục hoành, O là điểm cao nhất của đồ thị.
Xem thêm
Các dạng bài tập Đồ thị hàm số y = a.x^2 (có đáp án 2024) và cách giải - Toán 9
a) y = 2x – 6
Lời giải:
Cho x = 0 thì y = – 6, ta được giao điểm của đồ thị với trục Oy là A(0; – 6).
Cho y = 0 thì x = 3, ta được giao điểm của đồ thị với trục Ox là B(3; 0).
Đồ thị của hàm số y = 2x – 6 là đường thẳng AB.

b) y = –3x + 5
Lời giải:
Cho x = 0 thì y = 5, ta được giao điểm của đồ thị với trục Oy là M(0; 5).
Cho y = 0 thì x = , ta được giao điểm của đồ thị với trục Ox là N .
Đồ thị của hàm số y = –3x + 5 là đường thẳng MN.

c)
Lời giải:
Cho x = 0 thì y = 0, ta có đồ thị hàm số đi qua gốc tọa độ O(0; 0).
Cho x = 2 thì y = 3, ta có đồ thị hàm số đi qua điểm A(2; 3).
Đồ thị của hàm số là đường thẳng OA.

*Phương pháp giải:
Bước 1: Tìm tập xác định của hàm số.
Bước 2: Lập bảng giá trị (thường từ 3 đến 4 giá trị) tương ứng giữa x và y sao cho các điểm tương ứng nằm bên phải trục Oy.
Bước 3: Vẽ trục tọa độ Oxy và đánh dấu điểm O, các điểm đã lập trong bảng giá trị và các điểm đối xứng với chúng qua trục Oy.
Bước 4: Đồ thị hàm số y = a (a ≠ 0) luôn đi qua gốc tọa độ O và nhận trục Oy làm trục đối xứng. Vẽ đường cong parabol đi qua các điểm đã đánh dấu ta được đồ thị hàm số y = a (a ≠ 0) và kết luận.
*Lý thuyết:
- Đồ thị của hàm số: Đồ thị của hàm số y = a (a ≠ 0) là một parabol đi qua gốc tọa độ O, nhận Oy làm trục đối xứng (O là đỉnh của parabol)
+) Nếu a > 0 thì đồ thị nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị.
+) Nếu a < 0 thì đồ thị nằm phía dưới trục hoành, O là điểm cao nhất của đồ thị.
Xem thêm
Các dạng bài tập Đồ thị hàm số y = a.x^2 (có đáp án 2024) và cách giải - Toán 9
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hàm số bậc nhất y = 2x – 1.
Hoàn thành bảng giá trị sau vào vở:
x
–2
–1
0
1
2
y = 2x – 1
?
?
?
?
?
Cho hàm số bậc nhất y = 2x – 1.
Hoàn thành bảng giá trị sau vào vở:
|
x |
–2 |
–1 |
0 |
1 |
2 |
|
y = 2x – 1 |
? |
? |
? |
? |
? |
Câu 2:
Hàm chi phí đơn giản nhất là hàm chi phí bậc nhất y = ax + b, trong đó b biểu thị chi phí cố định của hoạt động kinh doanh và hệ số a biểu thị chi phí của mỗi mặt hàng được sản xuất. Giả sử rằng một xưởng sản xuất xe đạp có chi phí cố định hằng ngày là 36 triệu đồng và mỗi chiếc xe đạp có chi phí sản xuất là 1,8 triệu đồng.
a) Viết công thức của hàm số bậc nhất biểu thị chi phí y (triệu đồng) để sản xuất x (xe đạp) trong một ngày.
b) Vẽ đồ thị hàm số thu được ở câu a.
c) Chi phí để sản xuất 15 chiếc xe đạp trong một ngày là bao nhiêu?
d) Có thể sản xuất bao nhiêu chiếc xe đạp trong ngày, nếu chi phí trong ngày đó là 72 triệu đồng?
Hàm chi phí đơn giản nhất là hàm chi phí bậc nhất y = ax + b, trong đó b biểu thị chi phí cố định của hoạt động kinh doanh và hệ số a biểu thị chi phí của mỗi mặt hàng được sản xuất. Giả sử rằng một xưởng sản xuất xe đạp có chi phí cố định hằng ngày là 36 triệu đồng và mỗi chiếc xe đạp có chi phí sản xuất là 1,8 triệu đồng.
a) Viết công thức của hàm số bậc nhất biểu thị chi phí y (triệu đồng) để sản xuất x (xe đạp) trong một ngày.
b) Vẽ đồ thị hàm số thu được ở câu a.
c) Chi phí để sản xuất 15 chiếc xe đạp trong một ngày là bao nhiêu?
d) Có thể sản xuất bao nhiêu chiếc xe đạp trong ngày, nếu chi phí trong ngày đó là 72 triệu đồng?
Câu 3:
Trong hệ đo lường Mỹ, quãng đường thường được đo bằng dặm (mile) và 1 dặm bằng khoảng 1,609 km.
a) Viết công thức để chuyển đổi x (dặm) sang y (km). Công thức tính y theo x này có phải là một hàm số bậc nhất của x không?
b) Một ô tô chạy với vận tốc 55 dặm/giờ trên một quãng đường có quy định vận tốc tối đa là 80 km/h. Hỏi ô tô đó có vi phạm luật giao thông không?
Trong hệ đo lường Mỹ, quãng đường thường được đo bằng dặm (mile) và 1 dặm bằng khoảng 1,609 km.
a) Viết công thức để chuyển đổi x (dặm) sang y (km). Công thức tính y theo x này có phải là một hàm số bậc nhất của x không?
b) Một ô tô chạy với vận tốc 55 dặm/giờ trên một quãng đường có quy định vận tốc tối đa là 80 km/h. Hỏi ô tô đó có vi phạm luật giao thông không?
Câu 4:
Gọi A, B, C, D, E là các điểm trên đồ thị hàm số y = 2x – 1 có hoành độ x lần lượt là –2; –1; 0; 1; 2. Từ kết quả của HĐ4, hãy xác định tọa độ các điểm A, B, C, D, E.
Gọi A, B, C, D, E là các điểm trên đồ thị hàm số y = 2x – 1 có hoành độ x lần lượt là –2; –1; 0; 1; 2. Từ kết quả của HĐ4, hãy xác định tọa độ các điểm A, B, C, D, E.
Câu 5:
Đồng euro (EUR) là đơn vị tiền tệ chính thức ở một số quốc gia thành viên của Liên minh châu Âu. Vào một ngày, tỉ giá hối đoái giữa đồng euro và đồng đô la Mỹ (USD) là: 1 EUR = 1,1052 USD.
a) Viết công thức để chuyển đổi x euro sang y đô la Mỹ. Công thức tính y theo x này có phải là một hàm số bậc nhất của x không?
b) Vào ngày đó, 200 euro có giá trị bằng bao nhiêu đô la Mỹ?
c) Vào ngày đó, 500 đô la Mỹ có giá trị bằng bao nhiêu euro?
(Làm tròn kết quả của câu b,vc câu c đến hàng đơn vị).
Đồng euro (EUR) là đơn vị tiền tệ chính thức ở một số quốc gia thành viên của Liên minh châu Âu. Vào một ngày, tỉ giá hối đoái giữa đồng euro và đồng đô la Mỹ (USD) là: 1 EUR = 1,1052 USD.
a) Viết công thức để chuyển đổi x euro sang y đô la Mỹ. Công thức tính y theo x này có phải là một hàm số bậc nhất của x không?
b) Vào ngày đó, 200 euro có giá trị bằng bao nhiêu đô la Mỹ?
c) Vào ngày đó, 500 đô la Mỹ có giá trị bằng bao nhiêu euro?
(Làm tròn kết quả của câu b,vc câu c đến hàng đơn vị).
Câu 6:
Giá cước điện thoại cố định của một hãng viễn thông bao gồm cước thuê bao là 22 000 đồng/tháng và cước gọi là 800 đồng/ phút.
a) Lập công thức tính số điện cước điện thoại y (đồng) phải trả trong tháng khi gọi x phút.
b) Tính số tiền cước điện thoại phải trả khi gọi 75 phút.
c) Nếu số tiền cước điện thoại phải trả là 94 000 đồng thì trong tháng đó thuê bao đã gọi bao nhiêu phút.
Giá cước điện thoại cố định của một hãng viễn thông bao gồm cước thuê bao là 22 000 đồng/tháng và cước gọi là 800 đồng/ phút.
a) Lập công thức tính số điện cước điện thoại y (đồng) phải trả trong tháng khi gọi x phút.
b) Tính số tiền cước điện thoại phải trả khi gọi 75 phút.
c) Nếu số tiền cước điện thoại phải trả là 94 000 đồng thì trong tháng đó thuê bao đã gọi bao nhiêu phút.
Câu 7:
Cho hàm số bậc nhất y = ax + 3.
a) Tìm hệ số a, biết rằng khi x = 1 thì y = 5.
b) Với giá trị a tìm được, hãy hoàn thành bảng giá trị sau vào vở:
x
–2
–1
0
1
2
y
?
?
?
?
?
Cho hàm số bậc nhất y = ax + 3.
a) Tìm hệ số a, biết rằng khi x = 1 thì y = 5.
b) Với giá trị a tìm được, hãy hoàn thành bảng giá trị sau vào vở:
|
x |
–2 |
–1 |
0 |
1 |
2 |
|
y |
? |
? |
? |
? |
? |
Câu 8:
Một ô tô đi từ bến xe Giáp Bát (Hà Nội) đến thành phố Vinh (Nghệ An) với vận tốc 60 km/h. Hỏi sau t giờ ô tô đó cách trung tâm Hà Nội bao nhiêu kilômét? Biết rằng bến xe Giáp Bát cách trung tâm Hà Nội 7 km và coi rằng trung tâm Hà Nội, bến xe Giáp Bát và thành phố Vinh nằm trên cùng một đường thẳng.

Một ô tô đi từ bến xe Giáp Bát (Hà Nội) đến thành phố Vinh (Nghệ An) với vận tốc 60 km/h. Hỏi sau t giờ ô tô đó cách trung tâm Hà Nội bao nhiêu kilômét? Biết rằng bến xe Giáp Bát cách trung tâm Hà Nội 7 km và coi rằng trung tâm Hà Nội, bến xe Giáp Bát và thành phố Vinh nằm trên cùng một đường thẳng.

Câu 9:
Trong các hàm số sau, những hàm số nào là hàm số bậc nhất? Hãy xác định các hệ số a, b của chúng.
a) y = 0.x – 5;
b) y = 1 – 3x;
c) y = –0,6x;
d)
e) y = 2x2 + 1.
Trong các hàm số sau, những hàm số nào là hàm số bậc nhất? Hãy xác định các hệ số a, b của chúng.
a) y = 0.x – 5;
b) y = 1 – 3x;
c) y = –0,6x;
d)
e) y = 2x2 + 1.
Câu 11:
Xét bài toán mở đầu. Từ kết quả của HĐ2, hãy hoàn thành bảng sau vào vở:
t (giờ)
1
2
3
4
5
d (km)
?
?
?
?
?
Khoảng cách d có phải là một hàm số của thời gian t không?
Xét bài toán mở đầu. Từ kết quả của HĐ2, hãy hoàn thành bảng sau vào vở:
|
t (giờ) |
1 |
2 |
3 |
4 |
5 |
|
d (km) |
? |
? |
? |
? |
? |
Khoảng cách d có phải là một hàm số của thời gian t không?
Câu 12:
Xét bài toán mở đầu. Viết công thức tính quãng đường S đi được của ô tô sau t giờ. Quãng đường S có phải là một hàm số của thời gian t không?
Câu 13:
Xét bài toán mở đầu. Viết công thức tính khoảng cách d từ vị trí của ô tô đến trung tâm Hà Nội sau t giờ.
Xét bài toán mở đầu. Viết công thức tính khoảng cách d từ vị trí của ô tô đến trung tâm Hà Nội sau t giờ.
Câu 14:
Pi: Hàm số có phải là một hàm số bậc nhất không?
Vuông: Đây là hàm số bậc nhất.
Tròn: Không đúng, tớ nghĩ đây không phải hàm số bậc nhất.
Theo em, Vuông hay Tròn ai nói đúng? Vì sao?
Pi: Hàm số có phải là một hàm số bậc nhất không?
Vuông: Đây là hàm số bậc nhất.
Tròn: Không đúng, tớ nghĩ đây không phải hàm số bậc nhất.
Theo em, Vuông hay Tròn ai nói đúng? Vì sao?
Câu 15:
Trong các hàm số sau, những hàm số nào là hàm số bậc nhất?
a) y = 3x – 2;
b) y = –2x;
c) y = 2x2 + 3;
d) y = 3(x – 1);
e) y = 0x + 1.
Trong các hàm số sau, những hàm số nào là hàm số bậc nhất?
a) y = 3x – 2;
b) y = –2x;
c) y = 2x2 + 3;
d) y = 3(x – 1);
e) y = 0x + 1.











