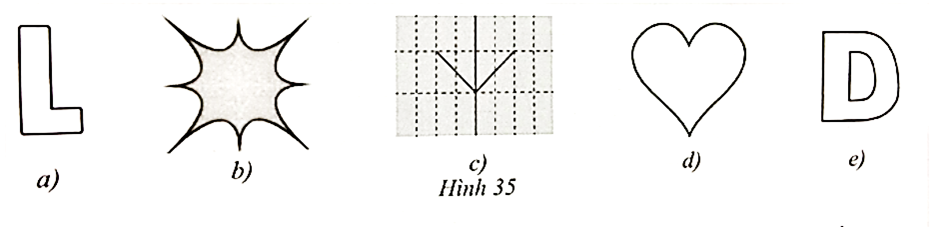
Câu hỏi:
23/07/2024 190Trong các câu sau, câu nào sai?
A. Hình vuông có 4 trục đối xứng.
B. Hình thoi, các góc khác 900 có đúng hai trục đối xứng.
C. Hình lục giác đều có đúng 3 trục đối xứng.
D. Hình chữ nhật có hai kích thước khác nhau có đúng hai trục đối xứng.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án C
Hình lục giác đều có tất cả 6 trục đối xứng
Do đó C sai.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hình bình hành ABCD có tâm O là tâm đối xứng. Biết OA = 5cm, OD = 7cm, tính độ dài hai đường chéo AC và BD
Câu 2:
Đoạn thẳng AB có độ dài 4cm. Gọi O là tâm đối xứng của đoạn thẳng AB. Tính độ dài đoạn OA.
Câu 3:
Trong các hình bên, em hãy chỉ ra:

a) Những hình có tâm đối xứng;
b) Những hình có trục đối xứng.
Câu 4:
Một chiếc bàn có mặt bàn là hình lục giác đều như hình dưới đây. Biết rằng độ dài đường chéo chính là 1,2m, em hãy tích khoảng cách từ tâm đối xứng của mặt bàn đến mỗi đỉnh và chu vi mặt bàn.
Câu 5:
Một hình tròn có bán kính 6cm, khoảng cách từ tâm đối xứng đến các điểm nằm trên đường tròn bằng:
Câu 6:
Hình thoi ABCD có tâm đối xứng O. Biết OA = 3cm, OB = 2cm. Hãy tính diện tích hình thoi.
Câu 8:
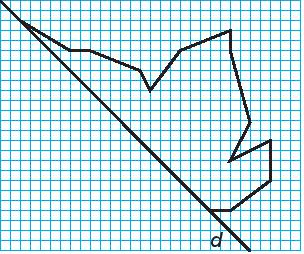
Vẽ chiếc lá
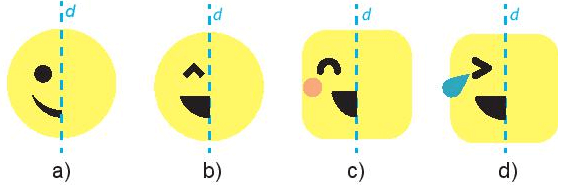
Vẽ hình bên vào giấy kẻ ô vuông rồi vẽ thêm và trang trí để được hình nhận đường thẳng d là trục đối xứng.
Câu 9:
Trong các phát biểu sau, có bao nhiêu phát biểu đúng?
a) Số trục đối xứng của tam giác đều nhỏ hơn số trục đối xứng của hình thoi.
b) Hình tròn có một trục đối xứng là đường thẳng đi qua tâm của hình tròn.
c) Hình thang cân có tâm đối xứng là giao điểm của hai đường chéo.
d) Hình chữ nhật có hai trục đối xứng là hai đường chéo.
Câu 10:
Nối cột A với cột B để được một phát biểu đúng.
|
Cột A |
|
Cột B |
|
Hình vuông |
|
không có trục đối xứng, cũng không có tâm đối xứng. |
|
Hình tròn |
không có trục đối xứng nhưng có tâm đối xứng. |
|
|
Hình thoi |
có vố số trục đối xứng. |
|
|
Hình thang |
có bốn trục đối xứng. |
|
|
Hình bình hành |
có hai trục đối xứng. |
Câu 13:
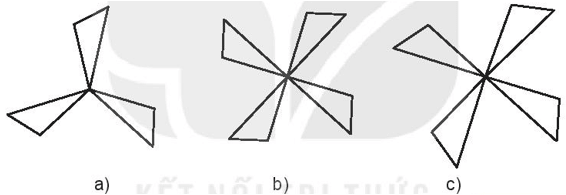
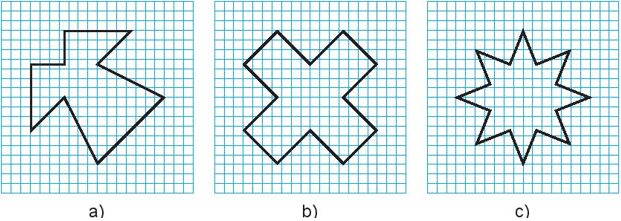
Em hãy vẽ các hình dưới đây vào giấy kẻ ô vuông rồi chỉ ra tất cả các trục đối xứng của chúng (nếu có)
Câu 14:
Vẽ các hình sau vào vở và vẽ thêm họa tiết để được hình mặt cười nhận đường thẳng d cho trước là trục đối xứng