Câu hỏi:
19/07/2024 394Tìm tất cả các giá trị thực của tham số m để phương trình sau có hai nghiệm thực phân biệt: (x+m−4)=0
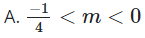
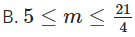
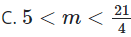
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án: C
Giải thích:
Lời giải:
log3(1−x2)+log13(x+m−4)=0
⇔{1−x2>0log3(1−x2)=log3(x+m−4)
Yêu cầu bài toán ∈(−1;1)
Dùng định lí về dấu tam thức bậc hai.
Để thỏa yêu cầu bài toán ta phải có phương trình −1<x1<x2<1
⇔{a.f(−1)>0a.f(1)>0Δ>0−1<S2<1
⇔{m−5>0m−3>021−4m>0
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 4:
Hỏi phương trình 3.2x+4.3x+5.4x=6.5x có tất cả bao nhiêu nghiệm thực?
Câu 6:
Với giá trị nào của x để hàm số y=22log3x−log23x đạt giá trị lớn nhất?
Câu 9:
Theo dự báo với mức tiêu thụ dầu không đổi như hiện nay thì trữ lượng dầu nước A sẽ hết sau 100 năm nữa. Nhưng do nhu cầu thực tế, mức tiêu thụ tăng lên 4% mỗi năm. Hỏi sau bao nhiêu năm số dầu dự trữ của nước A sẽ gần như hết (còn nhưng không đủ dùng cho năm tới)? Giả thiết nước này không nhập khẩu dầu từ nước khác.
Câu 10:
Cho (0;+∞) được cho trong hình vẽ bên. Khẳng định nào sau đây là đúng?
Câu 11:
Cho hệ phương trình {(23)2x−y+6(23)2x−y2−7=03log9(x−y)=1. Chọn khẳng định đúng?
Câu 14:
Hàm số nào trong hàm số sau đây có đồ thị phù hợp với hình vẽ bên?