Câu hỏi:
19/07/2024 94
Người ta dùng một đoạn dây thép và uốn nó thành hai hình vuông ABCD, MNPQ như Hình 2. Độ dài cạnh hình vuông MNPQ là x (cm). Độ dài cạnh hình vuông ABCD hơn ba lần độ dài cạnh hình vuông MNPQ là 3 cm. Sau khi uốn xong còn thừa đoạn dây thép ME dài 2 cm. Tìm x, biết độ dài đoạn dây thép đã dùng là 62 cm.
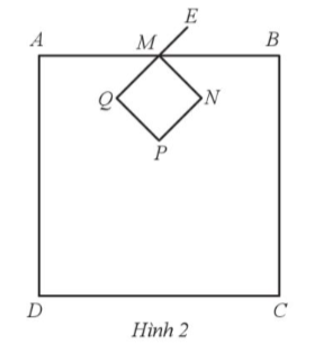
Người ta dùng một đoạn dây thép và uốn nó thành hai hình vuông ABCD, MNPQ như Hình 2. Độ dài cạnh hình vuông MNPQ là x (cm). Độ dài cạnh hình vuông ABCD hơn ba lần độ dài cạnh hình vuông MNPQ là 3 cm. Sau khi uốn xong còn thừa đoạn dây thép ME dài 2 cm. Tìm x, biết độ dài đoạn dây thép đã dùng là 62 cm.

Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Độ dài cạnh hình vuông MNPQ là x (cm).
Độ dài dây thép cần dùng để uốn thành hình vuông MNPQ là: 4x (cm).
Độ dài cạnh hình vuông ABCD là: 3x + 3 (cm).
Độ dài dây thép cần dùng để uốn thành hình vuông ABCD là: 4(3x + 3) (cm).
Do sau khi uốn xong còn thừa đoạn dây thép ME dài 2 cm và tổng độ dài đoạn dây thép đã dùng là 62 cm nên ta có phương trình:
4x + 4(3x + 3) + 2 = 62
4x + 12x + 12 + 2 = 62
16x = 62 ‒ 12 ‒ 2
16x = 48
x = 3
Vậy x = 3.
Độ dài cạnh hình vuông MNPQ là x (cm).
Độ dài dây thép cần dùng để uốn thành hình vuông MNPQ là: 4x (cm).
Độ dài cạnh hình vuông ABCD là: 3x + 3 (cm).
Độ dài dây thép cần dùng để uốn thành hình vuông ABCD là: 4(3x + 3) (cm).
Do sau khi uốn xong còn thừa đoạn dây thép ME dài 2 cm và tổng độ dài đoạn dây thép đã dùng là 62 cm nên ta có phương trình:
4x + 4(3x + 3) + 2 = 62
4x + 12x + 12 + 2 = 62
16x = 62 ‒ 12 ‒ 2
16x = 48
x = 3
Vậy x = 3.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 4:
b) Chứng tỏ x = ‒1 là nghiệm của phương trình (2) nhưng không là nghiệm của phương trình (1).
b) Chứng tỏ x = ‒1 là nghiệm của phương trình (2) nhưng không là nghiệm của phương trình (1).
Câu 5:
Kiểm tra xem số nào là nghiệm của phương trình tương ứng sau đây.
b) với x = 6; x = 9.
Kiểm tra xem số nào là nghiệm của phương trình tương ứng sau đây.
b) với x = 6; x = 9.
Câu 9:
Cho hai phương trình:
3(x ‒ 1) = 2x (1)
|x – 1| = 2 (2)
a) Chứng tỏ hai phương trình có nghiệm chung x = 3.
Cho hai phương trình:
3(x ‒ 1) = 2x (1)
|x – 1| = 2 (2)
a) Chứng tỏ hai phương trình có nghiệm chung x = 3.
Câu 13:
Kiểm tra xem số nào là nghiệm của phương trình tương ứng sau đây.
a) 6,36 ‒ 5,3x = 0 với x = ‒1,5; x = 1,2.
Kiểm tra xem số nào là nghiệm của phương trình tương ứng sau đây.
a) 6,36 ‒ 5,3x = 0 với x = ‒1,5; x = 1,2.
Câu 14:
Cho hai phương trình ẩn x:
3(x ‒ k) + k + 1 = 0 (1)
5x = 4(2x ‒ k) (2)
a) Xác định giá trị của k, biết phương trình (1) nhận x = 5 làm nghiệm.
Cho hai phương trình ẩn x:
3(x ‒ k) + k + 1 = 0 (1)
5x = 4(2x ‒ k) (2)
a) Xác định giá trị của k, biết phương trình (1) nhận x = 5 làm nghiệm.
Câu 15:
Tìm giá trị của t để mỗi phương trình có nghiệm tương ứng:
a) 3x + t = 0 có nghiệm x = ‒2;
Tìm giá trị của t để mỗi phương trình có nghiệm tương ứng:
a) 3x + t = 0 có nghiệm x = ‒2;











