Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là A
Lời giải
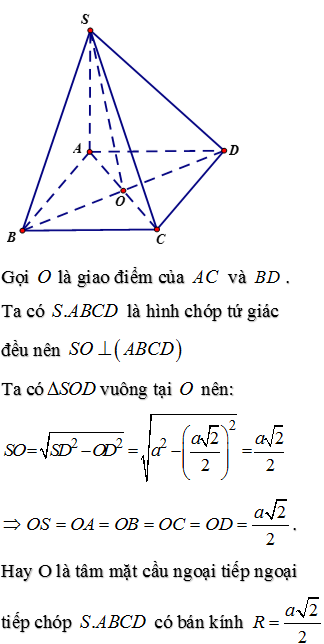
*Phương pháp giải:
a. Mặt cầu ngoại tiếp hình chóp.
+ Xác định trục d của đường tròn ngoại tiếp đa giác đáy (d là đường thẳng vuông góc với đáy tại tâm đường tròn ngoại tiếp đa giác đáy).
+ Xác định mặt phẳng trung trực (P) của một cạnh bên (hoặc trục Δ của của đường tròn ngoại tiếp một đa giác của mặt bên).
+ Giao điểm I của (P) và d (hoặc của Δ và d ) là tâm mặt cầu ngoại tiếp.
+ Kết luận: I là tâm mặt cầu ngoại tiếp chóp.
Nhận xét: Hình chóp có đáy hoặc các mặt bên là các đa giác không nội tiếp được đường tròn thì hình chóp đó không nội tiếp được mặt cầu.
*Lý thuyết:
Cho mặt cầu S(I; R)và đường thẳng a. Gọi H là hình chiếu của I lên a hay d (I; a) = IH. Nếu:
+) IH > R: a không cắt mặt cầu hay mặt cầu S(I; R)và đường thẳng a không có điểm chung.
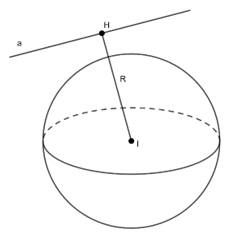
+) IH = R: a với mặt cầu S(I; R)có một điểm chung duy nhất là H. Ta nói a là một tiếp tuyến của mặt cầu S(I; R)và H là tiếp điểm.
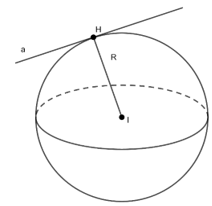
- Điều kiện cần và đủ để đường thẳng a tiếp xúc với mặt cầu S(I; R) tại điểm H là a vuông góc với bán kính OH tại điểm H đó.
+) IH < R: a cắt mặt cầu S(I; R) tại hai điểm A, B phân biệt.
Nhận xét: Tam giác IAB cân tại I, H là trung điểm của đoạn AB và
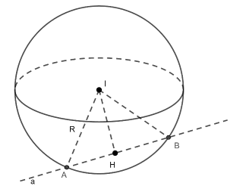
+) Đặc biệt: IH = 0: a đi qua tâm I của mặt cầu. Khi đó
- Định lí: Nếu điểm A nằm ngoài mặt cầu S(O; R) thì qua A có vô số tiếp tuyến với mặt cầu. Khi đó:
a. Độ dài các đoạn thẳng nối A với các tiếp điểm đều bằng nhau.
b. Tập hợp các tiếp điểm là một đường tròn nằm trên mặt cầu.
4. Vị trí tương đối giữa mặt cầu và mặt phẳng
Cho mặt cầu S(I; R)và mặt phẳng (P). Gọi H là hình chiếu vuông góc của I lên (P) hay . Nếu
+) IH > R: Mặt cầu S(I; R)và mặt phẳng (P) không có điểm chung
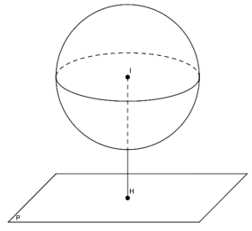
+) IH = R: Mặt phẳng (P) tiếp xúc mặt cầu S (I; R). Ta nói mặt phẳng (P) là mặt phẳng tiếp diện của mặt cầu và H là tiếp điểm
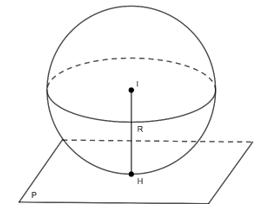
- Điều kiện để mặt phẳng (P) tiếp xúc với mặt cầu S(I; R)là: (P) vuông góc với bán kính IH tại điểm H.
+) IH < R: Mặt phẳng (P) cắt mặt cầu theo thiết diện là đường tròn có tâm
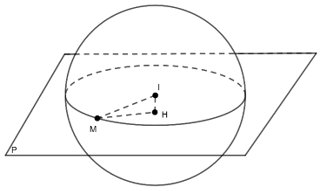
+) Đặc biệt: IH = 0 thì mặt phẳng (P) đi qua tâm I của mặt cầu, mặt phẳng đó gọi là mặt phẳng kính. Giao tuyến của mặt phẳng kính với mặt cầu là đường thẳng có bán kính R, đường tròn đó gọi là đường tròn lớn của mặt cầu.
5. Khái niệm mặt cầu nội tiếp, ngoại tiếp.
- Mặt cầu nội tiếp hình đa diện nếu mặt cầu đó tiếp xúc với tất cả các mặt của hình đa diện.
- Mặt cầu ngoại tiếp hình đa diện nếu tất cả các đỉnh của hình đa diện đều nằm trên mặt cầu.
6. Diện tích mặt cầu và thể tích khối cầu
Cho mặt cầu S(I; R).
Diện tích mặt cầu:
Thể tích khối cầu:
Chú ý:
- Diện tích S của mặt cầu bán kính R bằng bốn lần diện tích hình tròn lớn của mặt cầu đó.
- Thể tích V của khối cầu bán kính R bằng thể tích khối chóp có diện tích đáy bằng diện tích mặt cầu và có chiều cao bằng bán kính của khối cầu đó.
Xem thêm
50 bài toán về mặt cầu và phương pháp giải bài tập (có đáp án 2024) – Toán 12
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Tính bán kính R của mặt cầu ngoại tiếp một hình lập phương có cạnh bằng a.
Câu 3:
Trong không gian Oxyz, cho mặt cầu và 2 điểm A(-1;2;0), B(2;5;0). Gọi K(a;b;c) là điểm thuộc (S) sao cho KA+2KB nhỏ nhất. Giá trị a-b+c bằng
Câu 5:
Người ta làm tạ tập cơ tay như hình vẽ với hai đầu là hai khối trụ bằng nhau và tay cầm cũng là khối trụ. Biết hai đầu là hai khối trụ đường kính đáy bằng 12, chiều cao bằng 6, chiều dài tạ bằng 30 và bán kính tay cầm là 2. Hãy tính thể tích vật liệu làm nên tạ tay đó.
Câu 6:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt đáy và SA=a.
Mặt cầu ngoại tiếp hình chóp S.ABCD có bán kính bằng
Câu 7:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt phẳng (ABC) và SA=a. Diện tích của mặt cầu ngoại tiếp hình chóp S.ABC bằng
Câu 8:
Cho hình chóp S.ABC có SA,SB,SC đôi một vuông góc và SA=SB=SC=a. Tính bán kính r của mặt cầu nội tiếp hình chóp S.ABC (mặt cầu nội tiếp hình chóp là mặt cầu tiếp xúc với tất cả các mặt của hình chóp và có tâm nằm trong hình chóp).
Câu 9:
Một khối cầu có bán kính là 5(dm), người ta cắt bỏ hai phần của khối cầu bằng hai mặt phẳng song song cùng vuông góc với đường kính và cách tâm một khoảng 3 (dm) để làm một chiếc lu đựng nước (hình vẽ).
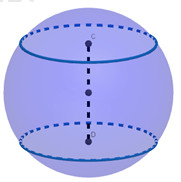
Tính thể tích nước tối đa mà chiếc lu có thể chứa được.
Câu 10:
Cho tứ diện ABCD có tam giác BCD vuông tại C, AB vuông góc với mặt phẳng (BCD), AB=5a, BC=3a và CD=4a. Tính bán kính R của mặt cầu ngoại tiếp tứ diện ABCD.
Câu 11:
Một khối đồ chơi gồm hai khối trụ , xếp chồng lên nhau, lần lượt có bán kính đáy và chiều cao tương ứng là , , , thỏa mãn , (tham khảo hình vẽ bên). Biết rằng thể tích của toàn bộ khối đồ chơi bằng 30, thể tích khối trụ bằng
Câu 12:
Cho tứ diện ABCD có CD=a,ABC là tam giác đều cạnh a, ACD vuông tại A. Mặt phẳng (BCD) vuông góc với mặt phẳng (ABD). Thể tích khối cầu ngoại tiếp tứ diện ABCD bằng
Câu 13:
Cho hình nón có đường sinh bằng đường kính đáy và bằng 2. Bán kính mặt cầu ngoại tiếp hình nón đó là.
Câu 14:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, cạnh SA vuông góc với mặt phẳng đáy, SA=10, AB=6, BC=8. Tính bán kính của mặt cầu ngoại tiếp hình chóp.
Câu 15:
Cho hình chóp S.ABC có SA(ABC), ABC là tam giác vuông tại A, AB=3a; AC=4a; SA=5a. Tìm bán kính mặt cầu mặt cầu ngoại tiếp hình chóp S.ABC?


