Câu hỏi:
23/07/2024 2,653Cho hàm số π6∫0f(x)dx bằng
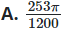
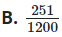
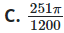
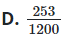
Đáp án chính xác
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án: D
Giải thích:
Lời giải
Ta có f(x)=∫cos2x.sin3xdx
=∫(2cos2x−1)(1−cos2x)sinxdx
Đặt t=cosx
⇒dt=−sinxdx
Khi đó: ∫(2cos2x−1)(1−cos2x)sinxdx
=−∫(2t2−1)(1−t2)dt
=∫(2t4−3t2+1)dt
=25t5−t3+t+C
=25cos5x−cos3x+cosx+C
Suy ra:
f(x)=25cos5x−cos3x+cosx+C
Mà f(π2)=0⇔C=0
Do đó
f(x)=25cos5x−cos3x+cosx
=cosx(25cos4x−cos2x+1)
=cosx[25(1−sin2x)2+sin2x]
I=π6∫0f(x) dx
=π6∫0cosx[25(1−sin2x)2+sin2x]dx
Đặt t=sinx⇒dt=cosxdx
Đổi cận
{x=0⇒t=0x=π6⇒t=12
I=12∫0[25(1−t2)2+t2]dt
=1512∫0(2t4+t2+2)dt
=15(25t5+13t3+2t)|120
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 3:
Với hai hàm số f(x) và g(x) liên tục trên [a ; b], k là một hằng số thực, khẳng định nào sau đây sai ?
Xem đáp án »
20/07/2024
1,275


