Câu hỏi:
20/07/2024 160Cho hai số phức z1,z2 thỏa mãn |z1-3i+5|=2 và |iz2-1+2i|=4.
Tìm giá trị lớn nhất của biểu thức T=|2iz1+3z2|
A. √313+16
B. √313
C. √313+8
D. √313+2√5
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A.
Phương pháp giải:
Đưa về biện luận vị trí giữa hai điểm thuộc đường tròn để khoảng cách của chúng lớn nhất
Lời giải:
Ta có ![]()
![]()
Và 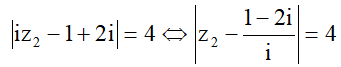
![]()
Đặt 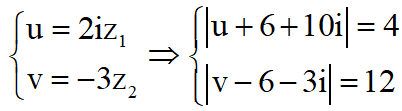
và ![]()
Tập hợp điểm M biểu diễn số phức u là đường tròn ![]() tâm I1(-6;-10),R1=4
tâm I1(-6;-10),R1=4
Tập hợp điểm N biểu diễn số phức v là đường tròn ![]() tâm I2(6;3), R2=4
tâm I2(6;3), R2=4
Khi đó ![]()
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho số phức thỏa mãn |(1+i)z+2|+|(1+i)z-2|=4√2.
Gọi m=max|z|; n=min|z| và số phức w=m+ni. Tính |w|2018.
Câu 2:
Cho số phức z=a+bi (a,b là các số thực) thỏa mãn z.ˉz+2z+i=0.
Tính giá trị của biểu thức T= a+b2
Câu 3:
Cho số phức z thỏa mãn |z|=1 .
Tìm giá trị lớn nhất của biểu thức T=|z+1|+2|z-1|
Câu 4:
Cho hai số phức z1,z2 có điểm biểu diễn lần lượt là M1,M2 cùng thuộc đường tròn có phương trình x2+y2=1 và .Tính giá trị biểu thức P=|z1+z2|
Câu 5:
Cho số phức z=a+bi với a,b là các số thực bất kỳ. Mệnh đề nào sau đây đúng?
Câu 6:
Biết z1 và z2 là hai nghiệm của phương trình 2z2+√3z+3=0 Khi đó giá trị của z21+z22 là
Câu 7:
Cho số phức z thỏa mãn |z-3-4i|=√5. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P=|z+2|2-|z-i|2. Tính môđun của số phức w= M+mi.
Câu 8:
Số phức z=a+bi(a,b∈ℝ) thỏa mãn |z-2|=|z| và (z+i)(ˉz-i) là số thực.
Giá trị của biểu thức S=a+2b bằng bao nhiêu?
Câu 9:
Gọi z1 là nghiệm phức có phần ảo âm của phương trình z2-2z+5=0 .
Tìm tọa độ điểm biểu diễn cho số phức 7-4iz1 trong mặt phẳng phức?
Câu 10:
Cho các số phức z1=3+2i, z2=3-2i.
Phương trình bậc hai có hai nghiệm z1 và z2 là:
Câu 12:
Cho số phức z thỏa mãn ![]() z(1-2i)+ˉzi=15+i
z(1-2i)+ˉzi=15+i
Tìm môđun của số phức z.
Câu 14:
Cho số phức z thỏa mãn |z-1z+3i|=1√2.
Tìm giá trị lớn nhất của biểu thức P=|z+i|+2|ˉz-4+7i|.


