Câu hỏi:
18/07/2024 203Cho ∆DEF vuông tại D. Gọi M, N, P lần lượt là trung điểm của DE, DF, EF.
a) Chứng minh tứ giác MNFE là hình thang.
b) Chứng minh tứ giác DMPN là hình chữ nhật.
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
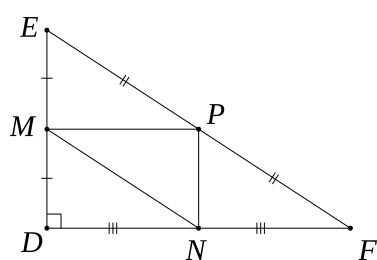
a) Xét tam giác DEF có:
M là trung điểm của DE
N là trung điểm của DF
⇒ MN là đường trung bình của tam giác DEF.
⇒ MN//EF, \(MN = \frac{1}{2}EF\)
⇒ MNFE là hình thang.
b) Xét tam giác DEF có:
M là trung điểm của DE
P là trung điểm của EF
⇒ MP là đường trung bình ΔDEF
⇒ MP//DF, \[MP = \frac{1}{2}DF\]
Lại có: N là trung điểm của DF
\[ \Rightarrow MP = DN = NF = \frac{1}{2}DF\]
Xét tứ giác DMPN có
MP = DN và MP//DN
⇒ DMPN là hình bình hành
Lại có: \[\widehat {EDF} = 90^\circ \]
⇒ DMPN là hình chữ nhật.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Phân tích đa thức thành nhân tử
a) 6x + 18;
b) 8x2y – 12xy2;
c) x2– 18x + 81;
d) x4y2+x4– 5y2– 5.
Câu 2:
Thực hiện phép tính
a) 4x(5x – 2);
b) 7x(3x2– 6x + 2);
c) (x – 5)(x – 7) – x2.
