Câu hỏi:
14/07/2024 118Cho các số phức z thỏa mãn . Tập hợp các điểm biểu diễn các số phức z trên mặt phẳng tọa độ là một đường thẳng. Viết phương trình đường thẳng đó
A. 4x+6y-3=0
B. 4x-6y-3=0
C. 4x+6y+3=0
D. 4x-6y+3=0
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn đáp án B.
Phương pháp: Tìm tập hợp các điểm biểu diễn số phức z thỏa mãn hệ thức cho trước
+ Đặt ![]()
+ Chuyển hệ thức với z về hệ thức với a, b, rút gọn để tìm hệ thức liên hệ giữa a và b
⇒ Phương trình (đường thẳng, đường tròn) cần tìm.
Cách giải
Giả sử ![]() . Ta có
. Ta có
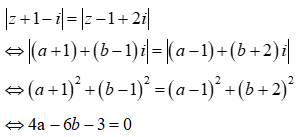
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho số phức z thỏa mãn: , với m là tham số thực thuộc .
Biết rằng tập hợp các điểm biểu diễn các số phức w=(3-4i)z-2i là một đường tròn.
Tính bán kính r nhỏ nhất của đường tròn đó.
Câu 2:
Trong số các số phức z thỏa mãn điều kiện gọi là số phức có mô đun lớn nhất. Khi đó là:
Câu 5:
Gọi P là điểm biểu diễn của số phức a+bi trong mặt phẳng phức.
Cho các mệnh đề sau:
(1) Môđun của a+bi là bình phương khoảng cách OP.
(2) Nếu P là biểu diễn của số 3+4i thì khoảng cách từ O đến P bằng 7.
Chọn đáp án đúng:
Câu 6:
Cho A, B, C là các điểm biểu diễn các số phức thỏa mãn . Tìm phát biểu sai:
Câu 8:
Cho hai số phức thỏa mãn và biểu thức đạt giá trị nhỏ nhất. Tính .
Câu 9:
Cho các số phức z, w thỏa mãn .
Giá trị nhỏ nhất của là
Câu 12:
Tập hợp các điểm trong mặt phẳng phức biểu diễn các số phức z thỏa mãn là:
Câu 13:
Với các số phức z thỏa mãn , tập hợp các điểm biểu diễn của số phức z là một đường tròn. Tìm bán kính R của đường tròn đó.
Câu 15:
Cho số phức z=a+bi với a, b là hai số thực khác 0. Một phương trình bậc hai với hệ số thực nhận làm nghiệm với mọi a, b là:


