Câu hỏi:
16/07/2024 146
a) Hình thoi có là hình bình hành không?
b) Cho hình thoi ABCD có O là giao điểm của hai đường chéo (Hình 13b). Các tam giác OAB, OCB, OCD, OAD có bằng nhau không?
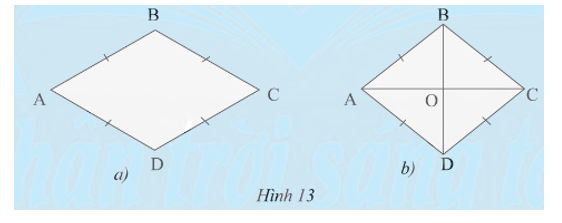
a) Hình thoi có là hình bình hành không?
b) Cho hình thoi ABCD có O là giao điểm của hai đường chéo (Hình 13b). Các tam giác OAB, OCB, OCD, OAD có bằng nhau không?

Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
a) Hình thoi có 4 cạnh bằng nhau AB = BC = CD = DA
Suy ra các cạnh đối cũng bằng nhau: AB = CD và AD = BC.
Do đó hình thoi cũng là hình bình hành.
b) Theo câu a, hình thoi ABCD cũng là hình bình hành.
Khi đó hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường.
Hay OA = OC và OB = OD.
Xét DOAB và DOAD có:
OA là cạnh chung; OB = OD; AB = AD
Do đó DOAB = DOAD (c.c.c) (1)
Chứng minh tương tự ta cũng có DOCB = DOCD (c.c.c) (2)
Xét DOAB và DOCD có:
OA = OC; (đối đỉnh); OB = OD
Do đó DOAB = DOCD (c.g.c) (3)
Từ (1), (2) và (3) ta có: DOAB = DOAD = DOCD = DOCB.
a) Hình thoi có 4 cạnh bằng nhau AB = BC = CD = DA
Suy ra các cạnh đối cũng bằng nhau: AB = CD và AD = BC.
Do đó hình thoi cũng là hình bình hành.
b) Theo câu a, hình thoi ABCD cũng là hình bình hành.
Khi đó hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường.
Hay OA = OC và OB = OD.
Xét DOAB và DOAD có:
OA là cạnh chung; OB = OD; AB = AD
Do đó DOAB = DOAD (c.c.c) (1)
Chứng minh tương tự ta cũng có DOCB = DOCD (c.c.c) (2)
Xét DOAB và DOCD có:
OA = OC; (đối đỉnh); OB = OD
Do đó DOAB = DOCD (c.g.c) (3)
Từ (1), (2) và (3) ta có: DOAB = DOAD = DOCD = DOCB.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hình bình hành ABCD, kẻ AH vuông góc với BD tại H và CK vuông góc với BD tại K (Hình 20).
a) Chứng minh tứ giác AHCK là hình bình hành.
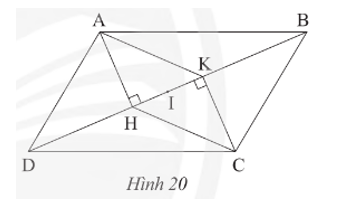
Cho hình bình hành ABCD, kẻ AH vuông góc với BD tại H và CK vuông góc với BD tại K (Hình 20).
a) Chứng minh tứ giác AHCK là hình bình hành.

Câu 4:
Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC.
a) Chứng minh rằng tứ giác EBFD là hình bình hành.
Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC.
a) Chứng minh rằng tứ giác EBFD là hình bình hành.
Câu 5:
Cần thêm một điều kiện gì để mỗi tứ giác trong Hình 19 trở thành hình bình hành?

Cần thêm một điều kiện gì để mỗi tứ giác trong Hình 19 trở thành hình bình hành?

Câu 6:
Tính độ dài cạnh của các khuy áo hình thoi có độ dài hai đường chéo lần lượt là 3,2 cm và 2,4 cm.
Tính độ dài cạnh của các khuy áo hình thoi có độ dài hai đường chéo lần lượt là 3,2 cm và 2,4 cm.

Câu 7:
Cho hình bình hành ABCD. Gọi I và K lần lượt là trung điểm của các cạnh AB và CD; E và F lần lượt là giao điểm của AK và CI với BD.
a) Chứng minh tứ giác AEFI là hình thang.
Cho hình bình hành ABCD. Gọi I và K lần lượt là trung điểm của các cạnh AB và CD; E và F lần lượt là giao điểm của AK và CI với BD.
a) Chứng minh tứ giác AEFI là hình thang.
Câu 9:
Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB tại E, tia phân giác của góc B cắt CD tại F.
a) Chứng minh DE // BF.
Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB tại E, tia phân giác của góc B cắt CD tại F.
a) Chứng minh DE // BF.
Câu 10:
b) Gọi E, F lần lượt là trung điểm của AB và AC, lấy điểm O sao cho E là trung điểm của OM. Chứng minh hai tam giác AOB và MBO vuông và bằng nhau.
b) Gọi E, F lần lượt là trung điểm của AB và AC, lấy điểm O sao cho E là trung điểm của OM. Chứng minh hai tam giác AOB và MBO vuông và bằng nhau.
Câu 11:
b) Gọi O là giao điểm của hai đường chéo của hình bình hành ABCD. Chứng minh rằng ba điểm E, O, F thẳng hàng.
b) Gọi O là giao điểm của hai đường chéo của hình bình hành ABCD. Chứng minh rằng ba điểm E, O, F thẳng hàng.
Câu 12:
Cho tứ giác ABCD có các cạnh đối song song. Gọi O là giao điểm của hai đường chéo. Hãy chứng tỏ:
‒ Tam giác ABC bằng tam giác CDA.
‒ Tam giác OAB bằng tam giác OCD.
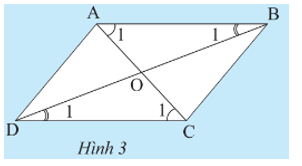
Cho tứ giác ABCD có các cạnh đối song song. Gọi O là giao điểm của hai đường chéo. Hãy chứng tỏ:
‒ Tam giác ABC bằng tam giác CDA.
‒ Tam giác OAB bằng tam giác OCD.

Câu 13:
Cho tam giác ABC cân tại A, gọi M là trung điểm của BC. Lấy điểm D đối xứng với điểm A qua BC.
a) Chứng minh tứ giác ABDC là hình thoi.

Cho tam giác ABC cân tại A, gọi M là trung điểm của BC. Lấy điểm D đối xứng với điểm A qua BC.
a) Chứng minh tứ giác ABDC là hình thoi.

Câu 14:
Cho hình thoi ABCD, hai đường chéo AC và BD cắt nhau tại O. Biết AC = 6 cm, BD = 8 cm. Tính độ dài cạnh của hình thoi ABCD.

Cho hình thoi ABCD, hai đường chéo AC và BD cắt nhau tại O. Biết AC = 6 cm, BD = 8 cm. Tính độ dài cạnh của hình thoi ABCD.

Câu 15:
Một tứ giác có chu vi là 52 cm và một đường chéo là 24 cm. Tìm độ dài của mỗi cạnh và đường chéo còn lại nếu biết hai đường chéo vuông góc tại trung điểm của mỗi đường.
Một tứ giác có chu vi là 52 cm và một đường chéo là 24 cm. Tìm độ dài của mỗi cạnh và đường chéo còn lại nếu biết hai đường chéo vuông góc tại trung điểm của mỗi đường.