TOP 10 đề thi Học kì 1 Toán 12 (Chân trời sáng tạo) 2024 có đáp án

Chỉ từ 150k mua trọn bộ Đề thi Toán 12 Học kì 1 Chân trời sáng tạo bản word có lời giải chi tiết:

B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và tài liệu.

Xem thử tài liệu tại đây: Link tài liệu

Đề thi Học kì 1 Toán 12 (Chân trời sáng tạo) có đáp án

Sở Giáo dục và Đào tạo ...

Đề thi Học kì 1 - Chân trời sáng tạo

Năm học ...

Môn: Toán 12

Thời gian làm bài: phút

(Đề 1)

PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.

Mỗi câu hỏi thí sinh chỉ chọn một phương án.

Câu 1. Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\) và có bảng biến thiên như hình vẽ sau

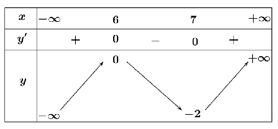
Tìm điểm cực đại của hàm số \(y = f\left( x \right)\).

A. \(x = 7\).

B. x = - 2.

C. \(x = 0\).

D. \(x = 6\).

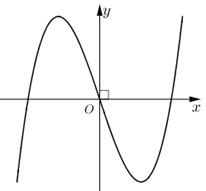
Câu 2. Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị là đường cong trong hình bên. Số nghiệm thực của phương trình \(f\left( x \right) = 1\) là

A. \(1\).

B. \(0\).

C. \(2\).

D. \(3\).

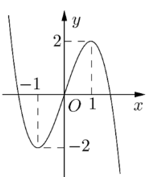
Câu 3. Cho hàm số \(y = \frac{{ax - 1}}{{bx + c}}\) với \(a,b,c \in \mathbb{R}\) có bảng biến thiên như hình vẽ:

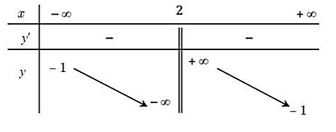
Hỏi trong ba số \(a,b,c\) có bao nhiêu số dương?

A. \(0\).

B. \(3\).

C. \(2\).

D. \(1\).

Câu 4. Cho hàm số \[y = \sqrt {2{x^2} + 1} \]. Mệnh đề nào dưới đây đúng?

A. Hàm số đồng biến trên khoảng \(\left( {0;\, + \infty } \right)\).

B. Hàm số đồng biến trên khoảng \(\left( { - \infty ;\,0} \right)\).

C. Hàm số nghịch biến trên khoảng \(\left( {0;\, + \infty } \right)\).

D. Hàm số nghịch biến trên khoảng \(\left( { - 1;\,1} \right)\).

Câu 5. Cho hình hộp chữ nhật \[ABCD.A'B'C'D'.\] Khẳng định nào sau đây đúng?

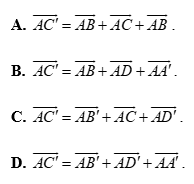
Câu 6. Trong không gian với hệ tọa độ \[Oxyz\]_, cho hai điểm \(M\left( {\frac{1}{2};1; - 3} \right)\) và \(N\left( {\frac{1}{2}; - 2;4} \right)\)_. Tọa độ của vectơ \[\overrightarrow {MN} \] là:

A. \(\left( {1; - 1;1} \right)\).

B. \(\left( {0; - 3;7} \right)\).

C. \(\left( {0;3; - 7} \right)\).

D. \(\left( {\frac{1}{2}; - \frac{1}{2};\frac{1}{2}} \right)\).

Câu 7. Cho biết máy bay \[A\] đang bay với vận tốc $\overrightarrow{u}=\left(300;200;400\right)$( đơn vị:\[{\rm{km/h)}}\]

Máy bay \[B\] ngược hướng và có tốc độ gấp 2 lần tốc độ của máy bay \[A\]. Tọa độ vectơ vận tốc \[\overrightarrow v \] của máy bay \[B\]là

Câu 8. Cho tứ diện \[ABCD\] có \[AB = AC = AD\] và \(\widehat {BAC} = \widehat {BAD} = 60^\circ \). Hãy xác định góc giữa cặp vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) ?

A. \(60^\circ \).

B. \[45^\circ \].

C. \[90^\circ \].

D. \[120^\circ \].

Câu 9. Trong không gian với hệ trục tọa độ \[Oxyz\], cho hai điểm \(A\left( {2;1;1} \right)\) và \(B\left( { - 1;2;1} \right)\). Tìm tọa độ \[A'\] đối xứng với \(A\) qua \(B\).

A. \(A'\left( {3;4; - 3} \right)\).

B.\(A'\left( { - 4;3;1} \right)\).

C. \(A'\left( {4; - 3;3} \right)\).

D. \(A'\left( {4;33} \right)\).

Câu 10. Trong không gian với hệ tọa độ Oxyz, cho các vectơ $\overrightarrow{a}=\left(1;2;3\right)$; $\overrightarrow{b}=\left(2;1;-3\right)$; $\overrightarrow{c}=\left(-1;1;5\right)$. Vectơ $\overrightarrow{x}=\overrightarrow{a}-4\overrightarrow{b}+2\overrightarrow{c}$ có tọa độ là:

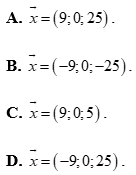
Câu 11. Một mẫu số liệu ghép nhóm có phương sai bằng 25 thì có độ lệch chuẩn bằng

A. \(4\).

B.\(5\).

C. \(256\).

D. \(50\).

Câu 12. Bảng sau thống kê khối lượng một số quả măng cụt được lựa chọn ngẫu nhiên trong một thùng hàng.

Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên (làm tròn đến hàng phần trăm) thuộc khoảng nào?

A. \(\left[ {4;5} \right)\).

B. \(\left[ {5;6} \right)\).

C. \(\left[ {6;7} \right)\).

D. \(\left[ {7;8} \right)\).

PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1. Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\mathbb{R}\) và có đồ thị như hình vẽ.

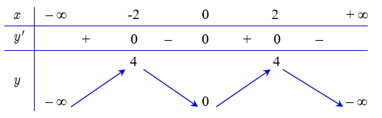
a) \(\mathop {\max }\limits_{{\rm{[}}0;2]} f(x) = 4\).

b) Hàm số \(y = f\left( x \right)\) có giá trị lớn nhất là 4 và giá trị nhỏ nhất là 0.

c) Hàm số \(y = f\left( {2\cos x} \right)\) có giá trị lớn nhất là 4 tại \(x = \frac{\pi }{2}\).

d) Không tồn tại giá trị lớn nhất của hàm số \(y = f\left( {f(x)} \right)\) trên \(\left( { - 2;2} \right)\).

Câu 2. Cho hàm số \[y = \frac{{{x^2} - 2x + 4}}{{x - 2}}\] có đồ thị \[\left( C \right)\]. Khi đó

a) Đồ thị hàm số có tiệm cận đứng là đường thẳng \[x = 2\].

b) Đồ thị hàm số có tiệm cận xiên là đường thẳng \[y = x\].

c) Tổng giá trị cực đại và giá trị cực tiểu của hàm số đã cho bằng \[4\].

d) Cho đường thẳng \[y = mx - 2\]. Khi đó có đúng 8 giá trị nguyên của tham số \[m\] không vượt quá 10 để đồ thị hàm số đã cho cắt đường thẳng \[y = mx - 2\] tại hai điểm phân biệt nằm về hai phía so với tiệm cận đứng của đồ thị \[\left( C \right)\].

Câu 3. Trong không gian với hệ trục tọa độ \(Oxyz\), cho ba điểm \(A\left( {1;2;3} \right),B\left( {2;1;5} \right),C\left( {2;4;2} \right).\)

a) Tọa độ trung điểm của \(AB\) là \(\left( {\frac{3}{2};\frac{3}{2};4} \right)\).

b) $\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\left(5;7;10\right)$

c) Góc giữa hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{AC}$ bằng \(30^\circ \).

d) Điểm \(I\left( {a;b;c} \right)\) nằm trên mặt phẳng \(\left( {Oxz} \right)\) thỏa mãn $\left|3\overrightarrow{IB}-\overrightarrow{IC}\right|$ đạt giá trị nhỏ nhất. Khi đó \(a - 2b + 2c = 15\).

Câu 4. Thống kê điểm thi khảo sát đầu năm môn Toán của hai lớp \(12A\) và \(12B\), ta thu được kết quả sau

a) Khoảng biến thiên của điểm thi của học sinh lớp \(12A\) và \(12B\) là như nhau.

b) Số điểm trung bình môn Toán trong bài khảo sát đầu năm của lớp \(12B\) lớn hơn của lớp \(12A.\)

c) Khoảng tứ phân vị của lớp \(12A\) lớn hơn 1.

d) Khoảng tứ phân vị của lớp \(12A\) lớn hơn so với lớp \(12B\).

PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời câu 1 đến câu 6.

Câu 1. Cho hàm số $y=-x^3-m{x}^2+\left(4m+9\right)x+5$, với m là tham số. Có bao nhiêu giá trị nguyên của \(m\) để hàm số nghịch biến trên \(\left( { - \infty ; + \infty } \right)\).

Câu 2. Ông A muốn mua một mảnh đất hình chữ nhật có diện tích bằng \(100\,{{\rm{m}}^{\rm{2}}}\)để làm khu vườn. Để chi phí xây dựng bờ rào xung quanh khu vườn là ít tốn kém nhất thì ông A đã mua mảnh đất có kích thước \(a({\rm{m}})\, \times \,b({\rm{m}})\)(với \(a\) là chiều dài, \(b\) là chiều rộng của khu vườn). Khi đó kết quả của \(a + 2b\) bằng bao nhiêu?

Câu 3. Một cửa hàng bán vải Thanh Hà với giá bán mỗi kg là 50000 đồng. Với giá bán này thì cửa hàng chỉ bán được khoảng 25 kg. Cửa hàng này dự định giảm giá bán, ước tính nếu cửa hàng cứ giảm 4000 đồng cho một kg thì số vải bán được tăng thêm là 50 kg. Xác định giá bán (đơn vị nghìn đồng) để cửa hàng đó thu được lợi nhuận lớn nhất, biết rằng giá nhập về ban đầu mỗi kg là 30000 đồng.

Câu 4. Trong không gian với hệ tọa độ \[Oxyz\], cho hình hộp \(ABCD.A'B'C'D'\) có \(A\left( {1;\,0;\,1} \right)\), \(B\left( {2;\,1;\,2} \right)\), \(D\left( {1;\, - 1;\,1} \right)\), \(C'\left( {4;\,5;\, - 5} \right)\). Giả sử \(A'\left( {a;b;c} \right)\). Tính \(a + b + c\).

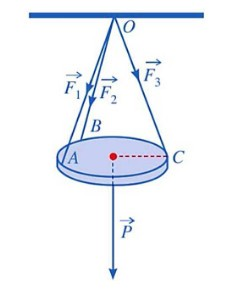
Câu 5. Một chiếc đèn trang trí hình tròn được treo song song với mặt phẳng trần nhà nằm ngang bởi ba sợi dây không giãn \(OA,\,OB,\,OC\) đôi một vuông góc (như hình vẽ dưới đây). Biết lực căng dây tương ứng trên mỗi dây \(OA,\,OB,\,OC\) lần lượt là \(\overrightarrow {{F_1}} ,\,\overrightarrow {{F_2}} ,\,\overrightarrow {{F_3}} \) thỏa mãn \[\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {{F_3}} } \right| = 16\](N). Tính trọng lượng (đơn vị: N) của chiếc đèn đó. (Làm tròn kết quả đến hàng phần mười).

Câu 6. Một công ty bất động sản Đất Vàng thực hiện cuộc khảo sát khách hàng xem họ có nhu cầu mua nhà ở mức giá nào để tiến hành dự án xây nhà ở Thăng Long group sắp tới. Kết quả khảo sát 500 khách hàng được ghi lại ở bảng sau:

Độ lệch chuẩn (làm tròn đến hàng phần mười) của mức giá đất là bao nhiêu ?

......................................................

......................................................

......................................................

=========================

Sở Giáo dục và Đào tạo ...

Đề thi Học kì 1 - Chân trời sáng tạo

Năm học ...

Môn: Toán 12

Thời gian làm bài: phút

(Đề 2)

PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.

Mỗi câu hỏi thí sinh chỉ chọn một phương án.

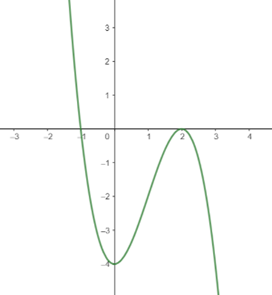
Câu 1. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?

A. y = x³ - 2024x.

B. y = -x³ + 3x.

C. y = x³ - 3x² + 2024.

D. y = -x³ + 3x² - 2.

Câu 2. Đồ thị hàm số $y=\frac{x+1}{x^2+x-2}$ có bao nhiêu đường tiệm cận đứng?

A. 1.

B. 3.

C. 2.

D. 4.

Câu 3. Giá trị lớn nhất của hàm số f(x) = $x+\frac{4}{x}$ trên (-4;0) là

A. -4.

B. 4.

C. -5.

D. 5.

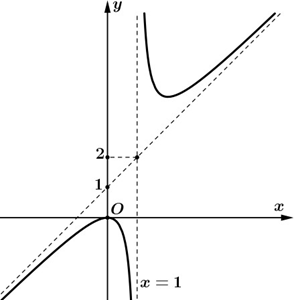
Câu 4. Cho hàm số $y=\frac{x^2+a}{x+b}$ có đồ thị là đường cong trong hình vẽ bên. Giá trị của T = a + b bằng

A. T = 0.

B. T = -2.

C. T = -1.

D. T = 2.

Câu 5. Cho hình lập phương ABCD.A'B'C'D'. Hai vectơ nào có giá cùng nằm trong mặt phẳng (ABCD).

A. $\overrightarrow{D{D}^{\text{'}}},\overrightarrow{AC}$.

B. $\overrightarrow{A{D}^{\text{'}}},\overrightarrow{AD}$.

C. $\overrightarrow{A{D}^{\text{'}}},\overrightarrow{AC}$.

D. $\overrightarrow{AC},\overrightarrow{AD}$.

Câu 6. Trong không gian Oxyz, cho biểu diễn của vectơ $\overrightarrow{a}$ qua các vectơ đơn vị là $\overrightarrow{a}=2\overrightarrow{i}+\overrightarrow{k}-3\overrightarrow{j}$. Tọa độ của vectơ $\overrightarrow{a}$ là

A. (2;-3;1).

B. (1;-3;2).

C. (2;1;-3).

D. (1;2;-3).

Câu 7. Trong không gian với hệ toạ độ Oxyz, cho điểm M(4;1;-2) và vectơ $\overrightarrow{u}=\left(4;-2;6\right)$. Tìm toạ độ điểm N biết rằng $\overrightarrow{MN}=-\frac{1}{2}\overrightarrow{u}$.

A. (2;2;5).

B. (2;-2;5).

C. (2;2;-5).

D. (-2;-2;5).

Câu 8. Cho tứ diện ABCD. Gọi G là trọng tâm tam giác BCD và điểm M thuộc cạnh AB sao cho AM = 2BM. Đẳng thức nào sau đây là đúng?

A. $\overrightarrow{MG}=\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}$.

B. $\overrightarrow{MG}=\frac{1}{3}\overrightarrow{AB}-\frac{1}{3}\overrightarrow{AC}-\frac{1}{3}\overrightarrow{AD}$.

C. $\overrightarrow{MG}=-\frac{1}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}+\frac{1}{3}\overrightarrow{AD}$.

D. $\overrightarrow{MG}=\frac{4}{3}\overrightarrow{AB}-\frac{1}{3}\overrightarrow{AC}-\frac{1}{3}\overrightarrow{AD}$.

Câu 9. Trong không gian Oxyz, cho A(4;0;0), B(0;2;0). Tâm đường tròn ngoại tiếp tam giác OAB

A. I (2;-1;0).

B. $I \left(\frac{4}{3};\frac{2}{3};0\right)$.

C. I (-2;1;0).

D. I (2;1;0).

Câu 10. Trong không gian Oxyz, cho ba điểm A(3;5;-1), B(7;x;1) và C(9;2;y). Để A, B, C thẳng hàng thì giá trị x + y bằng

A. 5.

B. 6.

C. 4.

D. 7.

Câu 11. Cho mẫu số liệu ghép nhóm có tứ phân vị thứ nhất, thứ hai, thứ ba lần lượt là Q₁, Q₂, Q₃. Khoảng tứ phân vị của mẫu số liệu ghép nhóm đó bằng:

A. Q₂ - Q₁.

B. Q₁ - Q₃.

C. Q₃ - Q₁.

D. Q₁ - Q₂.

Câu 12. Thời gian (phút) truy bài trước mỗi buổi học của một số học sinh trong một tuần được ghi lại ở bảng sau:

Nhóm chứa tứ phân vị thứ nhất là

A. [9;5;12;5).

B. [12;5;15;5).

C. [15;5;18;5).

D. [18;5;21;5).

PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1. Cho hàm số y = f(x) liên tục trên ℝ và có đồ thị như hình vẽ:

a) Hàm số đồng biến trên khoảng (0;2).

b) Hàm số đạt cực đại tại x = 0.

c) Giá trị nhỏ nhất của hàm số trên [-1;1] bằng -4.

d) Hàm số g(x) = f(3 - x) nghịch biến trên (2;5).

Câu 2. Xét tính đúng sai của các mệnh đề sau:

a) Hàm số $y=\frac{x^2-x+1}{x-1}$ đồng biến trên (2;+∞).

b) Cho hàm số y = f(x) có $f^{\text{'}}\left(x\right)=x^{2017}{\left(x-1\right)}^{2018}\left(x+1\right)\forall x\in ℝ$. Khi đó hàm số đã cho có 3 điểm cực trị.

c) Đồ thị hàm số $y=x^3-3x^2+2ax+b$ có điểm cực trị A(2;-2). Khi đó a + b = 2.

d) Một doanh nghiệp mua một chiếc máy giá 5000 (USD) để sản xuất x(kg) sản phẩm loại A. Trong thực tế, mỗi kg sản phẩm được sản xuất ra cần phải có nguyên liệu với giá 4 (USD). Khi doanh nghiệp này sản xuất một số lượng rất lớn sản phẩm thì chi phí để sản xuất được mỗi kg sản phẩm giảm dần và đạt giá trị nhỏ nhất là 4,1 (USD).

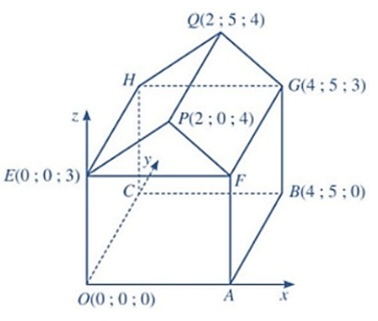
Câu 3. Hình minh họa sơ đồ một ngôi nhà trong không gian Oxyz, trong đó nền nhà, bốn bức tường và hai mái nhà đều là hình chữ nhật.

Xét tính đúng sai các mệnh đề sau:

a) Toạ độ điểm F(4;0;3).

b) Toạ độ vectơ $\overrightarrow{AH}=(4;5;3)$.

c) $\overrightarrow{AH}.\overrightarrow{AF}=3$.

d) Góc đốc của mái nhà, tức là số đo của góc nhị diện có cạnh là đường thẳng FG, hai mặt lần lượt là (FGQP) và (FGHE) bằng 26,6° (làm tròn kết quả đến hàng phần mười).

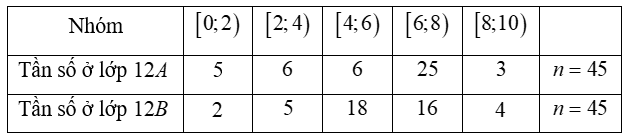
Câu 4. Kết quả môn Toán (cùng đề) của học sinh hai lớp 12A và 12B được cho lần lượt bởi mẫu số liệu ghép nhóm ở bảng sau:

a) Số trung bình cộng của hai mẫu số liệu trên bằng nhau.

b) Độ lệch chuẩn của mẫu số liệu lớp 12A nhỏ hơn 3.

c) Phương sai của mẫu số liệu lớp 12B lớn hơn 3.

d) Điểm thi của học sinh lớp 12B đồng đều hơn lớp 12A.

PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời câu 1 đến câu 6.

Câu 1. Tiệm cận xiên của đồ thị hàm số $y=f\left(x\right)=\frac{3x-x^2}{2x-1}$ là đường thẳng y = ax + b. Tính giá trị của biểu thức P = a² - b.

Câu 2. Chị Hà dự định sử dụng hết 4m² kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu mét khối (kết quả làm tròn đến hàng phần trăm)?

Câu 3. Quan sát một đàn ong trong 20 tuần, người ta ước lượng được số lượng ong trong đàn bởi công thức $P\left(t\right)=\frac{20000}{1+1000e^{-t}}$, trong đó t là thời gian tính theo tuần kể từ khi bắt đầu quan sát, 0 ≤ t ≤ 20. Tại thời điểm nào thì số lượng ong của đàn tăng nhanh nhất (kết quả làm tròn đến hàng đơn vị của tuần).

Câu 4. Trong một căn phòng dạng hình hộp chữ nhật với chiều dài 8m, rộng 6m và cao 4m có 2 cây quạt treo tường. Cây quạt A treo chính giữa bức tường 8m và cách trần 1m, cây quạt B treo chính giữa bức tường 6m và cách trần 1,5m. Chọn hệ trục tọa độ Oxyz như hình vẽ bên dưới ( đơn vị: mét). Giả sử $\overrightarrow{AB}=\left(a;b;c\right)$. Tính a + b + c.

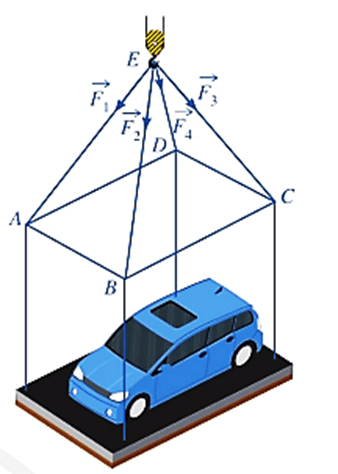
Câu 5. Một chiếc ô tô được đặt trên mặt đáy dưới của một khung sắt có dạng hình hộp chữ nhật với đáy trên là hình chữ nhật ABCD, mặt phẳng (ABCD) song song với mặt phẳng nằm ngang. Khung sắt đó được buộc vào móc E của chiếc cần cẩu sao cho các đoạn dây cáp EA, EB, EC và ED có độ dài bằng nhau và cùng tạo với mặt phẳng (ABCD) một góc bằng 60° (hình minh họa). Chiếc cần cẩu đang kéo khung sắt lên theo phương thẳng đứng.

Biết rằng các lực căng $\overrightarrow{F_1},\overrightarrow{F_2},\overrightarrow{F_3},\overrightarrow{F_4}$ đều có cường độ là 4,7kN và trọng lượng của khung sắt là 3kN. Trọng lượng lớn nhất của chiếc xe ô tô (làm tròn đến hàng phần mười) là bao nhiêu kN?

Câu 6. Chiều dài của 40 bé sơ sinh 12 ngày tuổi được chọn ngẫu nhiên ở viện nhi trung ương được nghiên cứu thống kê ở bảng dưới đây:

Tìm phương sai (làm tròn đến hàng phần trăm) của 40 bé sơ sinh ở bảng thống kê trên.

BẢNG ĐÁP ÁN

PHẦN I.

PHẦN II.

PHẦN III.

................................

................................

................................