Trắc nghiệm Xác suất thực nghiệm (có đáp án)
Trắc nghiệm Xác suất thực nghiệm (có đáp án)
-
253 lượt thi
-
21 câu hỏi
-
40 phút
Danh sách câu hỏi
Câu 1:
22/07/2024Sự kiện | Hai đồng sấp | Một đồng sấp, một đồng ngửa | Hai đồng ngửa |
Số lần | 22 | 20 | 8 |
Xác suất thực nghiệm của sự kiện “Có một đồng xu sấp, một đồng xu ngửa” là
 Xem đáp án
Xem đáp án
- Số lần tung là 50.
- Số lần sự kiện “Có một đồng xu sấp, một đồng xu ngửa” xảy ra là 20.
- Xác suất thực nghiệm của sự kiện trên là
20 : 50 = 0,4
Đáp án cần chọn là: B
Câu 2:
22/07/2024Sự kiện | Hai đồng sấp | Một đồng sấp, một đồng ngửa | Hai đồng ngửa |
Số lần | 22 | 20 | 8 |
Xác suất thực nghiệm của sự kiện “Hai đồng xu đều sấp”
 Xem đáp án
Xem đáp án
- Số lần tung là 50.
- Số lần sự kiện “Có một đồng xu sấp, một đồng xu ngửa” xảy ra là 22.
- Xác suất thực nghiệm của sự kiện trên là là 22 : 50 = 0,44.
Đáp án cần chọn là: C
Câu 3:
22/07/2024Mặt | 1 chấm | 2 chấm | 3 chấm | 4 chấm | 5 chấm | 6 chấm |
Số lần | 8 | 7 | 3 | 12 | 10 | 10 |
Hãy tính xác suất thực nghiệm của sự kiện gieo được mặt có số lẻ chấm trong 50 lần gieo trên.
 Xem đáp án
Xem đáp án
Tổng số lần gieo là 50.
Các mặt có số lẻ chấm của con xúc xắc là mặt 1, 3 và 5.
Số lần được mặt 1 chấm là 8 lần, mặt 3 chấm là 3 lần, mặt 5 chấm là 10 lần.
Số lần được mặt có số lẻ chấm là 8 + 3 + 10 = 21 lần
Xác suất thực nghiệm của sự kiện gieo được mặt có số lẻ chấm trong 50 lần là:\[\frac{{21}}{{50}} = 0,42\]
Đáp án cần chọn là: C
Câu 4:
22/07/2024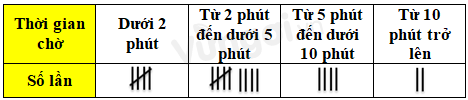
Hãy tính xác suất thực nghiệm của sự kiện “Sơn phải chờ xe dưới 2 phút”
 Xem đáp án
Xem đáp án
Tổng số lần Sơn chờ xe là 20 lần.
Số lần Sơn phải chờ xe dưới 2 phút là 5 lần.
Xác suất thực nghiệm của sự kiện “Sơn phải chờ xe dưới 2 phút” là:\[\frac{5}{{20}} = 0,25\]
Đáp án cần chọn là: D
Câu 5:
22/07/2024
Hãy tính xác suất thực nghiệm của sự kiện “Sơn phải chờ xe từ 5 phút trở lên”
 Xem đáp án
Xem đáp án
Tổng số lần Sơn chờ xe là 20 lần.
Số lần Sơn phải chờ xe từ 5 phút đến dưới 10 phút là: 4 lần
Số lần Sơn phải chờ xe từ 10 phút trở lên là: 2 lần
Số lần Sơn phải chờ xe từ 5 phút trở lên là: 4 + 2 = 6 lần.
Xác suất của sự kiện “Sơn phải chờ xe từ 5 phút trở lên”là: \[\frac{6}{{20}} = 0,3\]
Đáp án cần chọn là: A
Câu 6:
22/07/2024
Hãy tính xác suất thực nghiệm của sự kiện “Sơn phải chờ xe dưới 10 phút”
 Xem đáp án
Xem đáp án
Tổng số lần Sơn chờ xe là 20 lần.
Số lần Sơn phải chờ xe dưới 2 phút là 5 lần.
Số lần Sơn phải chờ xe từ 2 phút đến dưới 5 phút là 9 lần.
Số lần Sơn phải chờ xe từ 5 phút đến dưới 10 phút là 4 lần.
Số lần Sơn phải chờ xe dưới 10 phút là 5 + 9 + 4 = 18 lần.
Xác suất thực nghiệm của sự kiện “Sơn phải chờ xe dưới 10 phút”là:\[\frac{{18}}{{20}} = 0,9\]
Đáp án cần chọn là: C
Câu 7:
22/07/2024Màu bút | Bút xanh | Bút vàng | Bút đỏ |
Số lần | 14 | 10 | 16 |
Tính xác suất thực nghiệm của sự kiện lấy được màu đỏ
 Xem đáp án
Xem đáp án
Tổng số lần lấy là 40.
Số lần lấy được màu đỏ là 16.
Xác suất thực nghiệm của sự kiện lấy được màu đỏ là:\[\frac{{16}}{{40}} = 0,4\]
Đáp án cần chọn là: C
Câu 8:
22/07/2024Màu bút | Bút xanh | Bút vàng | Bút đỏ |
Số lần | 14 | 10 | 16 |
Tính xác suất thực nghiệm của sự kiện không lấy được màu vàng
 Xem đáp án
Xem đáp án
Tổng số lần lấy bút là 40.
Số lần lấy được màu vàng là 10
Số lần không lấy được màu vàng là 40 – 10 = 30.
Xác suất suất thực nghiệm của sự kiện không lấy được màu vàng là: \[\frac{{30}}{{40}} = 0,75\]
Đáp án cần chọn là: B
Câu 9:
23/07/2024Quý | Số ca xét nghiệm | Số ca dương tính |
I | 210 | 21 |
II | 150 | 15 |
III | 180 | 9 |
IV | 240 | 48 |
Xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính quý I” là
 Xem đáp án
Xem đáp án
Số ca xét nghiệm quý I là 210.
Số ca dương tính là 21 ca.
Xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính quý I” là \[\frac{{21}}{{210}} = 0,1\]
Đáp án cần chọn là: A
Câu 10:
22/07/2024Quý | Số ca xét nghiệm | Số ca dương tính |
I | 210 | 21 |
II | 150 | 15 |
III | 180 | 9 |
IV | 240 | 48 |
Có bao nhiêu quý có xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính” dưới 0,1?
 Xem đáp án
Xem đáp án
Bước 1:
Xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính” của quý I là \[\frac{{21}}{{210}} = 0,1\]
Xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính” của quý II là \[\frac{{15}}{{200}} = 0,075\]
Xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính” của quý III là \[\frac{9}{{180}} = 0,05\]
Xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính” của quý IV là \[\frac{{48}}{{240}} = 0,2\]
Bước 2:
Ta có hai số nhỏ hơn 0,1 là 0,05 và 0,075.
Vậy có 2 quý có xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính” dưới 0,1.
Đáp án cần chọn là: B
Câu 11:
22/07/2024Quý | Số ca xét nghiệm | Số ca dương tính |
I | 210 | 21 |
II | 150 | 15 |
III | 180 | 9 |
IV | 240 | 48 |
Xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính sau quý III tính từ đầu năm” là
 Xem đáp án
Xem đáp án
Số ca xét nghiệm sau quý III tính từ đầu năm là 210 + 150 + 180 = 540.
Số ca dương tính sau quý III tính từ đầu năm là 21 + 15 + 9 = 45.
Xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính sau quý III tính từ đầu năm” là \[\frac{{45}}{{540}} = \frac{1}{{12}}\]
Đáp án cần chọn là: C
Câu 12:
22/07/2024
Điền số thích hợp vào chỗ trống:
Kiểm tra thị lực của một học sinh trường THCS, ta thu được bảng kết quả như sau:
Khối | Số học sinh được kiểm tra | Số học sinh bị tật khúc xạ (cận thị, viễn thị, loạn thị) |
6 | 210 | 14 |
7 | 200 | 30 |
8 | 180 | 40 |
9 | 170 | 51 |
Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” khối 6 là…………, khối 7 là……………, khối 8 là …………, khối 9 là …………. Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” lớn nhất là khối ……….
 Xem đáp án
Xem đáp án
Lời giải:
Số học sinh bị khúc xạ khối 6 là 14. Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” khối 6 là \[\frac{{14}}{{210}} = \frac{1}{{15}}\] Số học sinh bị khúc xạ khối 7 là 30. Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” khối 7 là \[\frac{{30}}{{200}} = \frac{3}{{20}}\]
Số học sinh bị khúc xạ khối 8 là 40. Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” khối 8 là \[\frac{{40}}{{180}} = \frac{2}{9}\]
Số học sinh bị khúc xạ khối 9 là 51. Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” khối 9 là \[\frac{{51}}{{170}} = \frac{3}{{10}}\] Số lớn nhất trong các số \[\frac{1}{{15}};\frac{3}{{20}};\frac{2}{9};\frac{3}{{10}}\] .
Vậy khối có xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” lớn nhất là khối 9
Câu 13:
22/07/2024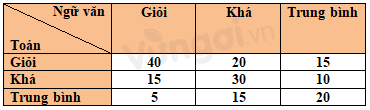
Ví dụ: Số học sinh có kết quả Toán – giỏi, Ngữ văn – giỏi là 40. Minh họa

Hãy tính xác suất thực nghiệm của sự kiện một học sinh được chọn ra một cách ngẫu nhiên có kết quả:iểu
Môn Toán đạt loại giỏi
 Xem đáp án
Xem đáp án
Tổng số học sinh là tổng tất cả các số trên bảng: 170.
Số học sinh được loại giỏi môn Toán là 40 + 20 + 15 = 75
Xác suất thực nghiệm của sự kiện một học sinh được chọn ra một cách ngẫu nhiên được loại giỏi môn Toán là \[\frac{{75}}{{170}} = \frac{{15}}{{34}}\]
Đáp án cần chọn là: A
Câu 14:
22/07/2024
Ví dụ: Số học sinh có kết quả Toán – giỏi, Ngữ văn – giỏi là 40. Minh họa

Hãy tính xác suất thực nghiệm của sự kiện một học sinh được chọn ra một cách ngẫu nhiên có kết quả:ụng
Loại khá trở lên ở cả hai môn
 Xem đáp án
Xem đáp án
Tổng số học sinh là tổng tất cả các số trên bảng: 170.
Các học sinh được loại khá trở lên ở cả 2 môn:
+ Toán giỏi, Ngữ văn giỏi: 40
+ Toán giỏi, Ngữ văn khá: 20
+ Toán khá, Ngữ văn giỏi: 15
+ Toán khá, Ngữ văn khá: 30
Số học sinh được loại khá trở lên ở cả 2 môn là:
40 + 20 + 15 + 30 = 105
Xác suất thực nghiệm của sự kiện một học sinh được chọn ra một cách ngẫu nhiên được loại khá trở lên ở cả 2 môn là \[\frac{{105}}{{170}} = \frac{{21}}{{34}}\]
Đáp án cần chọn là: C
Câu 15:
23/07/2024
Ví dụ: Số học sinh có kết quả Toán – giỏi, Ngữ văn – giỏi là 40. Minh họa

Hãy tính xác suất thực nghiệm của sự kiện một học sinh được chọn ra một cách ngẫu nhiên có kết quả:
Loại trung bình ở ít nhất một môn
 Xem đáp án
Xem đáp án
Tổng số học sinh là 170.
Các học sinh được loại trung bình ở ít nhất một môn là:
+ Toán trung bình, Văn giỏi: 5
+ Toán trung bình, Văn khá: 15
+ Toán trung bình, Văn trung bình: 20
+ Văn trung bình, Toán giỏi: 15
+ Văn trung bình, Toán khá: 10
Số học sinh được loại trung bình ở ít nhất một môn là:
5 + 15 + 20 + 15 + 10 = 65
Xác suất thực nghiệm của sự kiện một học sinh được chọn ra một cách ngẫu nhiên có kết quả được loại trung bình ít nhất một môn: \[\frac{{65}}{{170}} = \frac{{13}}{{34}}\]
Đáp án cần chọn là: B
Câu 16:
22/07/2024 Xem đáp án
Xem đáp án
Tổng số lần gieo là 22.
Số lần gieo được mặt N là 14.
Xác suất thực nghiệm xuất hiện mặt N là: \[\frac{{14}}{{22}} = \frac{7}{{11}}\]
Đáp án cần chọn là: A
Câu 17:
22/07/2024 Xem đáp án
Xem đáp án
Tổng số lần gieo là 30.
Số lần gieo được mặt S là 30 – 12 = 18.
Xác suất thực nghiệm xuất hiện mặt S là: \[\frac{{18}}{{30}} = \frac{3}{5}\]
Đáp án cần chọn là: C
Câu 18:
23/07/2024Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
Lần 1 | Số 3 | Lần 6 | Số 5 | Lần 11 | Số 3 | Lần 16 | Số 2 | Lần 21 | Số 1 |
Lần 2 | Số 1 | Lần 7 | Số 2 | Lần 12 | Số 2 | Lần 17 | Số 1 | Lần 22 | Số 5 |
Lần 3 | Số 2 | Lần 8 | Số 3 | Lần 13 | Số 2 | Lần 18 | Số 2 | Lần 23 | Số 3 |
Lần 4 | Số 3 | Lần 9 | Số 4 | Lần 14 | Số 1 | Lần 19 | Số 3 | Lần 24 | Số 4 |
Lần 5 | Số 4 | Lần 10 | Số 5 | Lần 15 | Số 5 | Lần 20 | Số 5 | Lần 25 | Số 5 |
Tính xác suất thực nghiệmiểu
Xuất hiện số 1
 Xem đáp án
Xem đáp án
Tổng số lần rút là 25 lần.
Số lần xuất hiện số 1 là 4 lần.
Xác suất thực nghiệm xuất hiện số 1 là \[\frac{4}{{25}} = 0,16\]
Đáp án cần chọn là: C
Câu 19:
22/07/2024Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
Lần 1 | Số 3 | Lần 6 | Số 5 | Lần 11 | Số 3 | Lần 16 | Số 2 | Lần 21 | Số 1 |
Lần 2 | Số 1 | Lần 7 | Số 2 | Lần 12 | Số 2 | Lần 17 | Số 1 | Lần 22 | Số 5 |
Lần 3 | Số 2 | Lần 8 | Số 3 | Lần 13 | Số 2 | Lần 18 | Số 2 | Lần 23 | Số 3 |
Lần 4 | Số 3 | Lần 9 | Số 4 | Lần 14 | Số 1 | Lần 19 | Số 3 | Lần 24 | Số 4 |
Lần 5 | Số 4 | Lần 10 | Số 5 | Lần 15 | Số 5 | Lần 20 | Số 5 | Lần 25 | Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số 2
 Xem đáp án
Xem đáp án
Tổng số lần rút là 25 lần.
Số lần xuất hiện số 2 là 6 lần.
Xác suất thực nghiệm xuất hiện số 2 là \[\frac{6}{{25}} = 0,24\]
Đáp án cần chọn là: B
Câu 20:
23/07/2024Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
Lần 1 | Số 3 | Lần 6 | Số 5 | Lần 11 | Số 3 | Lần 16 | Số 2 | Lần 21 | Số 1 |
Lần 2 | Số 1 | Lần 7 | Số 2 | Lần 12 | Số 2 | Lần 17 | Số 1 | Lần 22 | Số 5 |
Lần 3 | Số 2 | Lần 8 | Số 3 | Lần 13 | Số 2 | Lần 18 | Số 2 | Lần 23 | Số 3 |
Lần 4 | Số 3 | Lần 9 | Số 4 | Lần 14 | Số 1 | Lần 19 | Số 3 | Lần 24 | Số 4 |
Lần 5 | Số 4 | Lần 10 | Số 5 | Lần 15 | Số 5 | Lần 20 | Số 5 | Lần 25 | Số 5 |
Tính xác suất thực nghiệmụng
Xuất hiện số chẵn
 Xem đáp án
Xem đáp án
Tổng số lần rút là 25 lần.
Số lần xuất hiện số 2 là 6 lần.
Số lần xuất hiện số 4 là 3 lần.
Số lần xuất hiện số chẵn là 6 + 3 = 9 lần.
Xác suất thực nghiệm xuất hiện số 2 là \[\frac{9}{{25}} = 0,36\]
Đáp án cần chọn là: C
Câu 21:
22/07/2024 Xem đáp án
Xem đáp án
Tổng số lần gieo là 20, số lần xuất hiện mặt 3 chấm là 6 lần.
Xác suất thực nghiệm xuất hiện mặt 3 chấm bằng \[\frac{6}{{20}} = 0,3\]
Đáp án cần chọn là: B
Có thể bạn quan tâm
- Trắc nghiệm Xác suất thực nghiệm (có đáp án) (252 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Phép thử nghiệm – Sự kiện (có đáp án) (281 lượt thi)
- Trắc nghiệm Bài tập ôn tập chương 9: Một số yếu tố thống kê (có đáp án) (236 lượt thi)
