Trắc nghiệm Toán 10 CTST Bài 3. Các phép toán trên tập hợp có đáp án (Vận dụng)
-
555 lượt thi
-
5 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
22/07/2024
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
⦁ Xét tập hợp A:
Ta có .
Û 2x ≥ x2 + 1 (do x2 + 1 > 0)
Û x2 – 2x + 1 ≤ 0.
Û (x – 1)2 ≤ 0.
Mà (x – 1)2 ≥ 0 với mọi x.
Nên (x – 1)2 ≤ 0 Û x – 1 = 0
Û x = 1 ∈ ℝ.
Vì vậy A = {1}.
⦁ Xét tập hợp B:
Xét phương trình x2 – 2bx + 4 = 0 (*)
∆’ = b2 – 4.
Phương trình (*) vô nghiệm Û ∆’ < 0.
Û b2 – 4 < 0.
Û –2 < b < 2.
Vì b là số nguyên nên ta nhận b = –1; b = 0; b = 1.
Suy ra tập B = {–1; 0; 1}.
Tập A ∩ B = {1}.
Vậy số phần tử chung của tập A và tập B là 1 phần tử.
Do đó ta chọn phương án A.
Câu 2:
17/07/2024Cho ba tập hợp A = [–2; 2], B = [1; 5], C = [0; 1]. Khi đó tập (A \ B) ∩ C là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Để xác định tập hợp A \ B, ta vẽ sơ đồ sau đây:
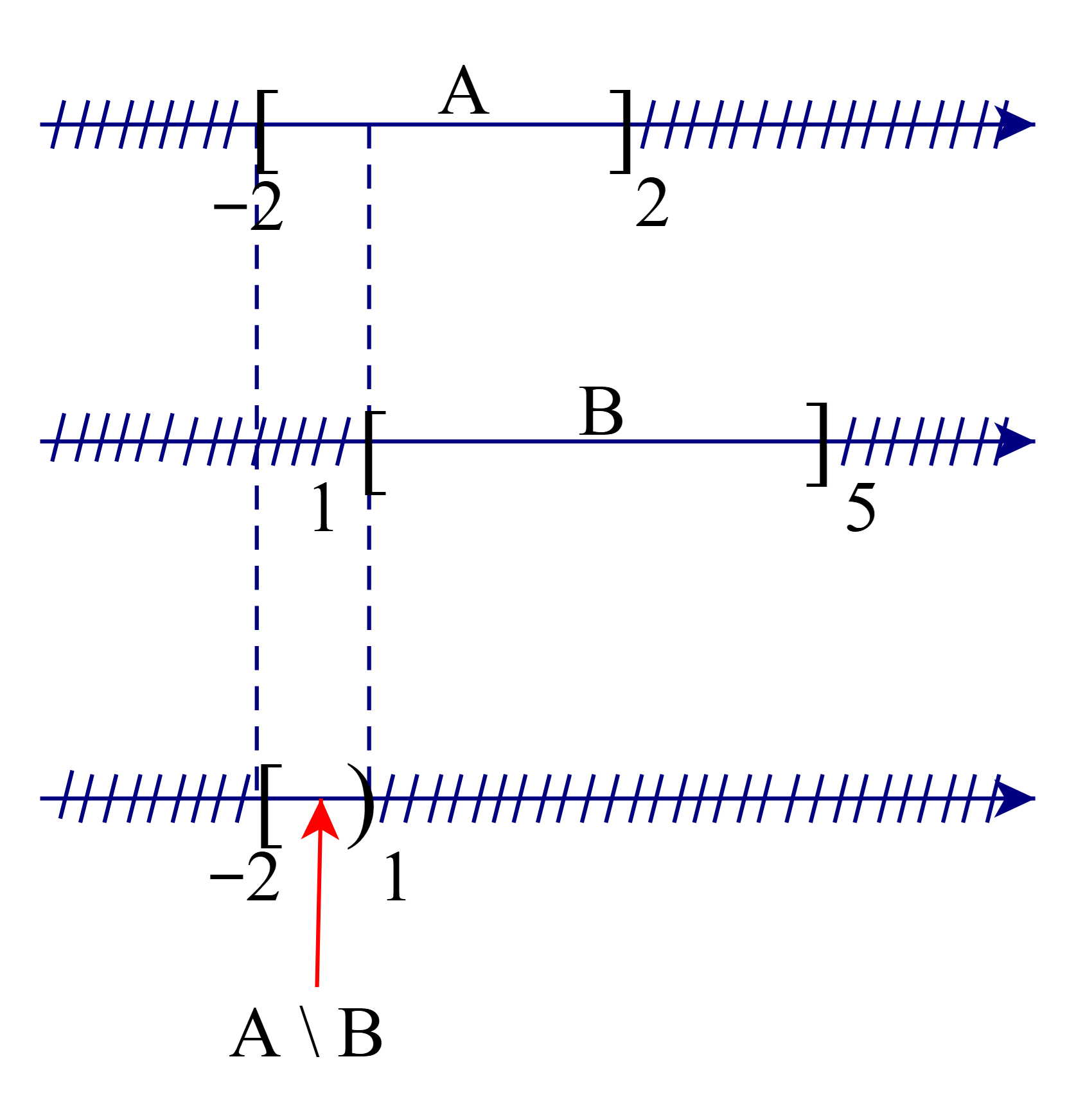
Từ sơ đồ, ta thấy A \ B = [–2; 1) (vì tập B chứa số 1 nên phần bù sẽ không lấy số 1).
Để xác định tập hợp (A \ B) ∩ C, ta vẽ sơ đồ sau đây:
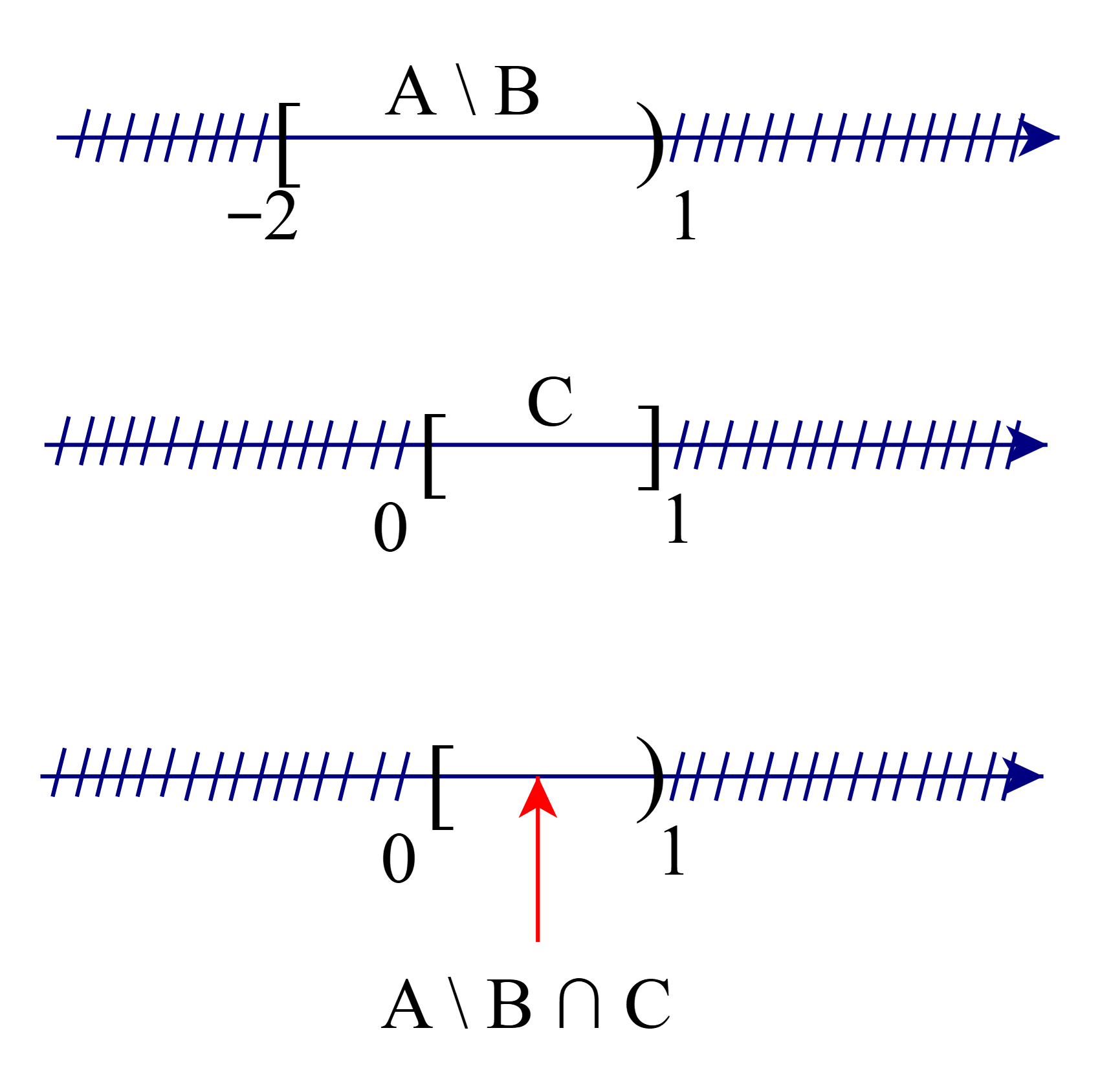
Từ sơ đồ, ta thấy (A \ B) ∩ C = [0; 1) (giao tức là lấy phần chung, tuy tập C có số 1 nhưng vì tập A \ B không lấy số 1 nên ta không lấy số 1).
Vậy ta chọn phương án B.
Câu 3:
14/07/2024 Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
⦁ Ta có x + 2 ≥ 0.
Û x ≥ –2.
Do đó tập A = [–2; +∞).
⦁ Ta có 5 – x ≥ 0.
Û x ≤ 5.
Do đó tập B = (–∞; 5].
Để xác định tập hợp A \ B, ta vẽ sơ đồ sau đây:
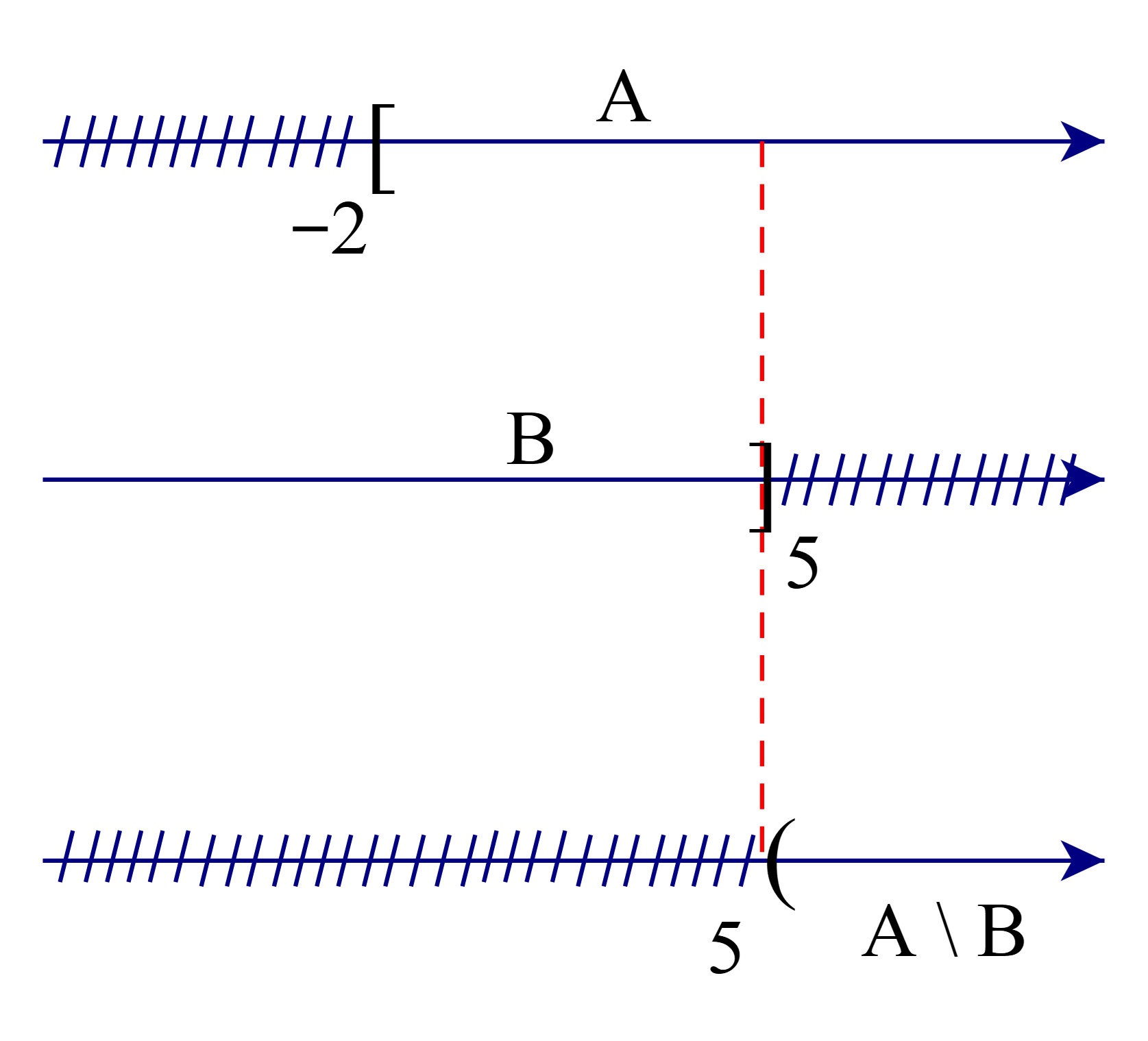
Từ sơ đồ, ta thấy A \ B = (5; +∞) (vì tập B có số 5 nên phần bù sẽ không lấy số 5).
Vậy ta chọn phương án C.
Câu 4:
14/07/2024Cho hai tập khác rỗng A = (m – 1; 4], B = (–2; 2m + 2), m ∈ ℝ. Tìm m để A ∩ B ≠ ∅.
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Vì tập A khác rỗng nên ta có m – 1 < 4.
Û m < 5 (1)
Vì tập B khác rỗng nên ta có –2 < 2m + 2.
Û –4 < 2m.
Û m > –2 (2)
Từ (1) và (2), ta suy ra tập hợp A và B đều khác rỗng khi và chỉ khi –2 < m < 5 (*).
Để A ∩ B ≠ ∅ thì m – 1 < 2m + 2.
Nghĩa là, m > –3 (**).
Giao (*) và (**) lại với nhau, ta thu được kết quả –2 < m < 5.
Vậy ta chọn phương án C.
Câu 5:
18/07/2024 Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Gọi T, L, K lần lượt là tập hợp các học sinh giỏi Toán, tập hợp các học sinh giỏi Lý và tập học các học sinh không giỏi môn nào cả.
Theo đề, ta có:
⦁ n(T) = 25;
⦁ n(L) = 23;
⦁ n(T ∩ L) = 14;
⦁ n(K) = 6.
Ta có sơ đồ Ven biểu diễn 3 tập hợp T, L, K như sau:
Khi đó số học sinh cả lớp là: n(T ∪ L) + n(K).
Ta có n(T ∪ L) = n(T) + n(L) – n(T ∩ L) = 25 + 23 – 14 = 34.
Vậy số học sinh cả lớp là: 34 + 6 = 40 (học sinh).
Do đó ta chọn phương án B.