Giải SBT Toán học 11 CTST Bài 5: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện
Giải SBT Toán học 11 CTST Bài 5: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện
-
65 lượt thi
-
4 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
16/07/2024Cho hình chóp S.ABC có đáy là hình vuông tâm O cạnh a, SA = và vuông góc với đáy. Xác định và tính góc giữa:
a) SB và (ABCD);
b) SC và (ABCD);
c) SD và (ABCD);
d) SB và (SAC).
 Xem đáp án
Xem đáp án
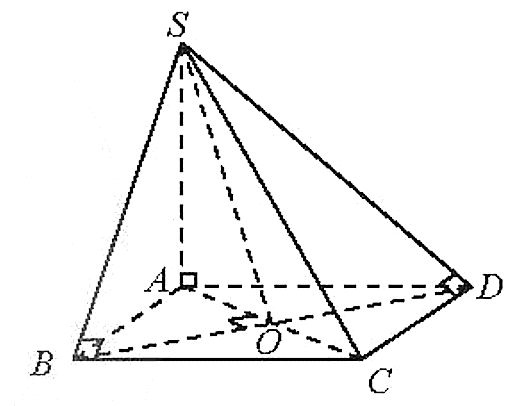
a) Ta có:
Suy raAB là hình chiếu của SB trên (ABCD).
Do đó (SB, (ABCD)) = (SB, AB).
Trong tam giác SAB vuông tại A, ta có:
Vậy
b) Tương tự câu a) ta xác định được (SC, (ABCD)) = (SC, AC).
Trong tam giác SAC vuông tại A, ta có:
Vậy
c) Tương tự câu a) ta xác định được (SD, (ABCD)) = (SD,AD).
Trong tam giác SAD vuông tại A, ta có:
Vậy
d) Ta có:
Þ BD ^ (SAC) hay BO ^ (SAC). (1)
Mà SB Ç (SAC) = S. (2)
Từ (1) và (2) suy ra SO là hình chiếu của SB trên (SAC).
Do đó: (SB, (SAC)) = (SB, SO).
Trong tam giác SBO vuông tại O, ta có:
Vậy
Câu 2:
15/07/2024Cho hình chóp S.ABC có đáy là tam giác đều cạnh bằng 3. Hình chiếu vuông góc của S trên mặt phẳng đáy trùng với trung điểm I của cạnh AB. Biết rằng mặt bên (SAB) là tam giác vuông cân tại S. Xác định và tính góc giữa:
a) SA và (ABC);
b) SC và (SAB).
 Xem đáp án
Xem đáp án
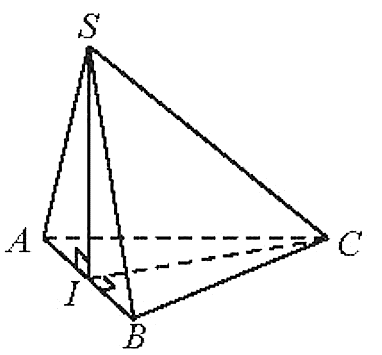
a) Vì AI là hình chiếu của SA trên (ABC).
Do đó (SA, (ABC)) = (SA, AI).
Vì tam giác SAI vuông cân tại I
Vậy
b) Ta có tam giác ABC đều nên CI ^ AB,
Ta có:
Mà SC Ç (SAB) = S. (2)
Từ (1) và (2) Þ SI là hình chiếu của SC trên (SAB).
Do đó (SC, (SAB)) = (SC, SI).
Trong tam giác SAB vuông tại S,
Trong tam giác SCI vuông tại I, ta có
Vậy
Câu 3:
07/07/2024Cho hình chóp tam giác đều S.ABC, cạnh đáy bằng a, cạnh bên bằng . Tính số đo góc phẳng nhị diện [S, BC, A].
 Xem đáp án
Xem đáp án
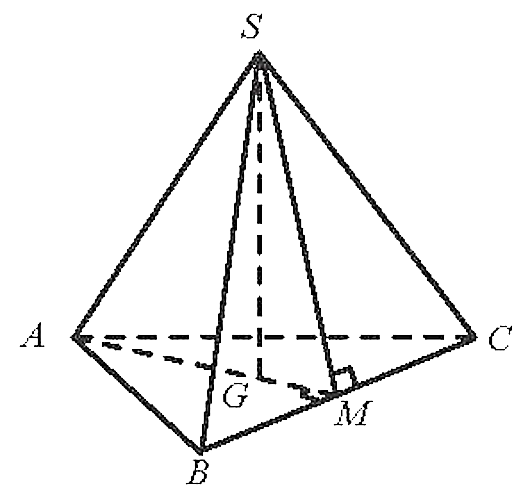
Gọi M là trung điểm BC, G là trọng tâm tam giác ABC.
Ta có SG ^ (ABC), SM ^ BC, AM ^ BC.
Suy ra là góc phẳng nhị diện [S, BC, A].
Ta tính được
Þ GM = SG.
Ta có tam giác SMG vuông cân tại G, suy ra số đo góc phẳng nhị diện [S, BC, A] =
Câu 4:
17/07/2024Cho hình chóp S.ABC có SA ^ (ABC). Tam giác ABC vuông tại A, , AC = a, . Tính số đo góc phẳng nhị diện [S, BC, A].
 Xem đáp án
Xem đáp án
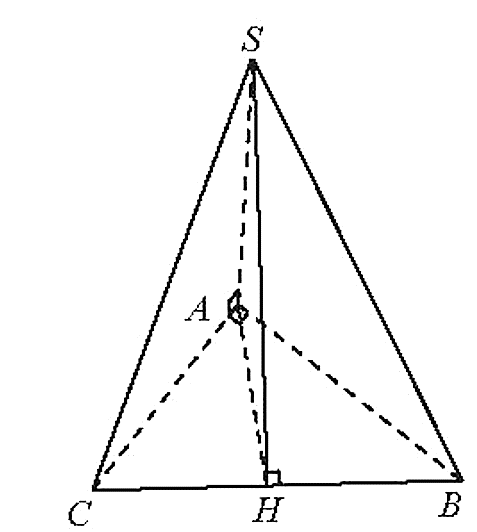
Vẽ AH ^ BC (H Î BC), ta có SH ^ BC.
Suy ra là góc phẳng nhị diện [S, BC, A].
Ta có AH = AC.sin60° = = SA
Do đó = 45°.
