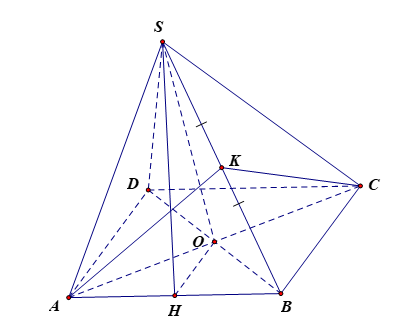
a) Gọi O là giao điểm của AC và BD nên O là trung điểm của AC, BD.

Xét tam giác SAC có SA = SC nên tam giác SAC cân tại S mà SO là trung tuyến nên SO là đường cao hay SO $\perp$ AC.

Xét tam giác SBD có SD = SB nên tam giác SBD cân tại S mà SO là trung tuyến nên SO là đường cao hay SO $\perp$ BD.

Do đó SO $\perp$ (ABCD) nên SO $\perp$ AB.

Kẻ OH $\perp$ AB tại H mà SO $\perp$ AB. Khi đó AB $\perp$ (SOH). Suy ra AB $\perp$ SH.

Do đó góc giữa hai mặt phẳng (SAB) và mặt phẳng (ABCD) bằng góc giữa hai đường thẳng SH và HO mà $\left(SH,HO\right)=\widehat{SHO}$.

Xét tam giác ABC có OH là đường trung bình nên $OH=\frac{BC}{2}=\frac{a}{2}$.

Xét tam giác SAH vuông tại H, có $AH=\frac{AB}{2}=\frac{a}{2};SA=a$.

Khi đó $SH=\sqrt{S{A}^2-A{H}^2}=\sqrt{a^2-{\left(\frac{a}{2}\right)}^2}=\frac{a\sqrt{3}}{2}$.

Xét tam giác SHO vuông tại O, có $cos\widehat{SHO}=\frac{OH}{SH}=\frac{\sqrt{3}}{3}$.

Vậy côsin góc giữa hai mặt phẳng (SAB) và (ABCD) là $\frac{\sqrt{3}}{3}$.

b) Gọi K là trung điểm của SB.

Xét tam giác SAB đều có AK là trung tuyến nên AK đồng thời là đường cao.

Suy ra AK $\perp$ SB.

Xét tam giác SCB đều có CK là trung tuyến nên CK đồng thời là đường cao.

Suy ra CK $\perp$ SB.

Do đó góc giữa hai mặt phẳng (SAB) và mặt phẳng (SBC) bằng góc giữa hai đường thẳng AK và CK.

Ta có AK, CK là đường cao của các tam giác đều cạnh a nên $AK=CK=\frac{a\sqrt{3}}{2}$.

Xét tam giác ABC vuông tại B, có AC² = AB² + BC² = a² + a² = 2a² ⇒$a\sqrt{2}$.

Áp dụng định lí côsin trong tam giác ACK, ta có:

$cos\widehat{AKC}=\frac{A{K}^2+C{K}^2-A{C}^2}{2\cdot AK\cdot CK}=-\frac{1}{3}$, suy ra $cos\left(AK,CK\right)=-cos\widehat{AKC}=\frac{1}{3}$.

Vậy côsin góc giữa hai mặt phẳng (SAB) và mặt phẳng (SBC) bằng $\frac{1}{3}$.

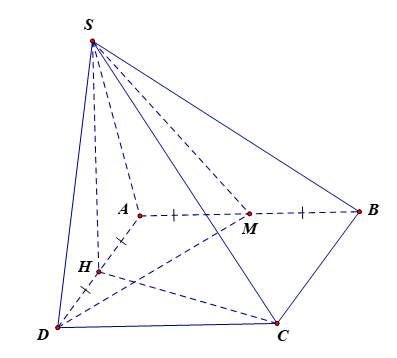
a) Vì tam giác SAD đều, SH là trung tuyến nên SH là đường cao hay SH $\perp$ AD.

Ta có (SAD) $\perp$ (ABCD) và SH $\perp$ AD nên SH $\perp$ (ABCD).

Suy ra CH là hình chiếu vuông góc của SC trên mặt phẳng (ABCD).

Khi đó góc giữa đường thẳng SC và mặt đáy (ABCD) bằng góc giữa hai đường thẳng SC và CH, mà .

Vì tam giác SAD đều cạnh a, SH là đường cao nên $SH=\frac{a\sqrt{3}}{2}$.

Xét tam giác DHC vuông tại D, có $HC=\sqrt{D{C}^2+D{H}^2}=\sqrt{a^2+{\left(\frac{a}{2}\right)}^2}=\frac{a\sqrt{5}}{2}$.

Xét tam giác SHC vuông tại H, có $SC=\sqrt{S{H}^2+C{H}^2}=\sqrt{\frac{3a^2}{4}+\frac{5a^2}{4}}=a\sqrt{2},cos\widehat{SCH}=\frac{HC}{SC}=\frac{\sqrt{10}}{4}$.

Vậy côsin của góc giữa đường thẳng SC và mặt đáy (ABCD) bằng $\frac{\sqrt{10}}{4}$.

b) Vì ABCD là hình vuông nên AB = AD mà M, H lần lượt là trung điểm của AB và AD nên DH = HA = AM = MB.

Xét DCDH và DDAM có: CD = DA; $\widehat{CDH}=\widehat{DAM}=90°$; DH = AM.

Do đó DCDH = DDAM.

Vì DCDH = DDAM suy ra $\widehat{CHD}=\widehat{DMA}$.

Do đó $\widehat{HDM}+\widehat{DHC}=\widehat{HDM}+\widehat{DMA}=90°$. Suy ra DM ^ CH.

Vì SH $\perp$ (ABCD) nên SH $\perp$ DM mà DM $\perp$ CH. Do đó DM $\perp$ (SCH).

Mà DM $\subset$ (SMD) nên (SMD) $\perp$ (SHC).

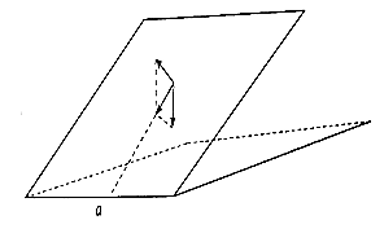
Gọi a là giao tuyến của mặt phẳng nằm ngang và mặt phẳng nằm nghiêng. Phương của lực hút Trái Đất vuông góc với mặt phẳng nằm ngang, phương của phản lực vuông góc với mặt phẳng nghiêng nên phương của hai lực nói trên đều vuông góc với đường thẳng a. Do đó, đường thẳng a vuông góc với mặt phẳng (P) chứa hai phương của hai lực đó. Vì tổng hợp lực của trọng lực và phản lực là một lực có phương nằm trên mặt phẳng (P) nên phương đó vuông góc với a. Do đó, viên bi lăn dọc theo đường thẳng vuông góc với đường thẳng a.