Giải SBT Toán 11 CTST Bài 2. Biến cố hợp và quy tắc cộng xác suất
Giải SBT Toán 11 CTST Bài 2. Biến cố hợp và quy tắc cộng xác suất
-
70 lượt thi
-
15 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
19/07/2024Trong một cuộc gặp mặt có 63 đoàn viên tham dự, trong đó có 25 người đến từ miền bắc, 19 người đến từ miền Nam và 19 người đến từ miền Trung.
a) Gặp ngẫu nhiên 1 đoàn viên trong cuộc gặp mặt, tính xác suất của biến cố “Đoàn viên được gặp đến từ miền Nam hoặc miền Trung”.
 Xem đáp án
Xem đáp án
a) Không gian mẫu của phép thử là .
Xác suất của biến cố “Đoàn viên được gặp đến từ miền Nam” là .
Xác suất của biến cố “Đoàn viên được gặp đến từ miền Trung” là .
Xác suất của biến cố “Đoàn viên được gặp đến từ miền Nam hoặc miền Trung” là:
.
Câu 2:
13/07/2024b) Gặp ngẫu nhiên 2 đoàn viên trong cuộc gặp mặt, tính xác suất của biến cố “Hai đoàn viên được gặp cùng đến từ miền Bắc hoặc cùng đến từ miền Nam”.
 Xem đáp án
Xem đáp án
b) Không gian mẫu của phép thử là
Số trường hợp xảy ra của biến cố “ Hai đoàn viên được gặp cùng đến từ miền Bắc” là .
Xác suất của biến cố “ Hai đoàn viên được gặp cùng đến từ miền Bắc” là
.
Số trường hợp xảy ra của biến cố “ Hai đoàn viên được gặp cùng đến từ miền Nam” là .
Xác suất của biến cố “ Hai đoàn viên được gặp cùng đến từ miền Nam” là
.
Xác suất của biến cố “Hai đoàn viên được gặp cùng đến từ miền Bắc hoặc cùng đến từ miền Nam” là
.
Câu 3:
20/07/2024Một túi chứa 2 viên bi xanh, 5 viên bi đỏ và 3 viên bi vàng có cùng kích thước và khối lượng. Chọn ra ngẫu nhiên 3 viên bi từ túi. Tính xác suất của các biến cố:
a) “Cả 3 viên bi lấy ra đều có cùng màu”.
 Xem đáp án
Xem đáp án
a) Không gian mẫu của phép thử là
Số trường hợp xảy ra của biến cố “Cả 3 viên bi lấy ra đều có màu đỏ” là .
Xác suất của biến cố “Cả 3 viên bi lấy ra đều có màu đỏ” là
.
Số trường hợp xảy ra của biến cố “Cả 3 viên bi lấy ra đều có màu đỏ” là .
Xác suất của biến cố “Cả 3 viên bi lấy ra đều có màu vàng” là
.
Xác suất của biến cố “Cả 3 viên bi lấy ra đều có cùng màu” là
.
Câu 4:
18/07/2024b) “Có không quá 1 viên bi xanh trong 3 viên bi lấy ra”.
 Xem đáp án
Xem đáp án
b) Số trường hợp xảy ra của biến cố “Không có viên bi xanh nào được lấy ra” là .
Xác suất của biến cố “Không có viên bi xanh nào được lấy ra” là
.
Số trường hợp xảy ra của biến cố “Không có viên bi xanh nào được lấy ra” là .
Xác suất của biến cố “Chỉ có một viên bi xanh được lấy ra” là
.
Xác suất của biến cố “Có không quá 1 viên bi xanh trong 3 viên bi lấy ra” là
.
Câu 5:
21/07/2024c) “Có đúng 2 màu trong 3 viên bi lấy ra”.
 Xem đáp án
Xem đáp án
c) Gọi A là biến cố “Có đúng 2 màu trong 3 viên bi lấy ra”; B là biến cố “Cả 3 viên bi lấy ra có cùng màu” và C là biến cố “3 viên bi lấy ra có cả 3 màu”.
Ta thấy . Khi đó: ;
Số trường hợp xảy ra của biến cố C là .
.
Do B và C là hai biến cố xung khắc nên
.
Vậy xác suất của biến cố “Có đúng 2 màu trong 3 viên bi lấy ra” là .
Câu 6:
21/07/2024Thanh có 4 tấm thẻ được đánh số 1, 3, 4, 7. Thanh lấy ra 3 trong 4 thẻ và xếp chúng thành một hàng ngang một cách ngẫu nhiên để tạo thành một số có 3 chữ số. Tính xác suất của biến cố A: “Số tạo thành chia hết cho 2 hoặc 3”.
 Xem đáp án
Xem đáp án
Không gian mẫu của phép thử là (số).
Gọi B là biến cố “Số tạo thành chia hết cho 2”, C là biến cố “Số tạo thành chia hết cho 3”.
Do đó, BC là biến cố “Số tạo thành chia hết cho 6”.
Biến cố B xảy ra khi chữ số hàng đơn vị của số tạo thành là 4, có thể xếp được số chia hết cho 2 nên .
Biến cố B xảy ra khi 3 chữ số của số tạo thành là 1, 4, 7, có thể xếp được số chia hết cho 3 nên .
Có thể tạo thành 2 số chia hết cho 6 là 714 và 174 nên .
Vậy .
Câu 7:
18/07/2024Cho A và B là hai biến cố độc lập với nhau.
a) Biết P(A) = 0,4 và P( ) = 0,3. Tính xác suất của các biến cố B và .
b) Biết P( ) = 0,4 và P( ) = 0,9. Tính xác suất của các biến cố A, B và AB.
 Xem đáp án
Xem đáp án
Vì A và B là hai biến cố độc lập nên và B; A và ; và cũng độc lập.
a) Ta có .
• và B độc lập nên .
• A và B độc lập nên
![]() .
.
Câu 8:
15/07/2024b) Biết P( ) = 0,4 và P( ) = 0,9. Tính xác suất của các biến cố A, B và AB.
 Xem đáp án
Xem đáp án
b) Vì và B độc lập nên
Hay .
Khi đó
.
Với ;
Câu 9:
15/07/2024Một hộp chứa 10 quả bóng xanh và 10 quả bóng đỏ có kích thước và khối lượng như nhau. Lấy ra ngẫu nhiên đồng thời 5 quả bóng từ hộp. Sử dụng sơ đồ hình cây, tính xác suất của biến cố “Có ít nhất 3 quả bóng xanh trong 5 quả bóng lấy ra”.
 Xem đáp án
Xem đáp án
Không gian mẫu của phép thử là .
Sơ đồ hình cây số trường hợp của các biến cố:
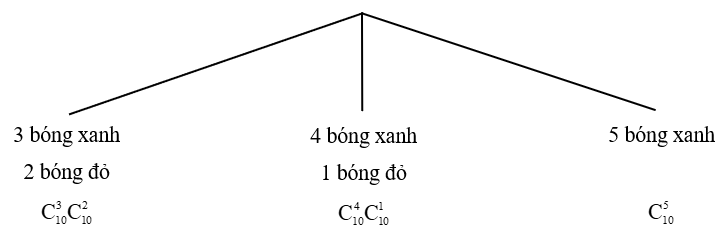
Khi đó, xác suất của biến cố “Có ít nhất 3 quả bóng xanh trong 5 quả bóng lấy ra” là:
.
Vậy xác suất của biến cố “Có ít nhất 3 quả bóng xanh trong 5 quả bóng lấy ra” là
Câu 10:
06/07/2024Châu gieo một con xúc xắc cân đối và đồng chất liên tiếp cho đến khi xuất hiện mặt 6 chấm thì dừng lại. Sử dụng sơ đồ hình cây, tính xác suất của biến cố “Châu phải gieo không quá 3 lần để xuất hiện mặt 6 chấm”.
 Xem đáp án
Xem đáp án
Sơ đồ hình cây:

Xác suất của biến cố “Châu phải gieo không quá 3 lần để xuất hiện mặt 6 chấm” là:
.
Vậy xác suất của biến cố “Châu phải gieo không quá 3 lần để xuất hiện mặt 6 chấm” là .
Câu 11:
17/07/2024Trong một trò chơi, Dương chọn ra 5 số từ 100 số tự nhiên đầu tiên. Sau đó, người ta chọn ra ngẫu nhiên 3 số may mắn từ 100 số tự nhiên đầu tiên đó. Tính xác suất của các biến cố:
A: “Không có số may mắn nào trong 5 số Dương đã chọn”;
B: “Có đúng 1 số may mắn trong 5 số Dương đã chọn”.
 Xem đáp án
Xem đáp án
Không gian mẫu của phép thử là
Biến cố A xảy ra khi 3 số may mắn nằm trong 95 số mà Dương không chọn. Số trường hợp xảy ra của biến cố A là .
Do đó xác suất của biến cố A là: .
Biến cố B xảy ra khi trong 3 số may mắn, có 1 số Dương đã chọn, 2 số còn lại nằm trong 95 số mà Dương không chọn. Số trường hợp xảy ra của biến cố B là .
Do đó, xác suất của biến cố B là: .
Câu 12:
23/07/2024Một hộp chứa 3 quả bóng xanh và một số quả bóng đỏ có cùng kích thước và khối lượng. Lấy ra ngẫu nhiên 2 quả bóng từ hộp. Biết rằng xác suất của biến cố “Lấy được 2 quả bóng đỏ” gấp 5 lần xác suất của biến cố “Lấy được 2 quả bóng xanh”. Tính xác suất của biến cố “Lấy được 2 quả bóng có cùng màu”.
 Xem đáp án
Xem đáp án
Gọi n là số quả bóng đỏ trong hộp. Tổng số quả bóng trong hộp là n+3 quả.
Không gian mẫu của phép thử là
Số trường hợp xảy ra của biến cố “Lấy được 2 quả bóng xanh” là .
Xác suất lấy được 2 quả bóng xanh là .
Số trường hợp xảy ra của biến cố “Lấy được 2 quả bóng đỏ” là .
Xác suất lấy được 2 quả bóng đỏ là .
Theo đề bài, ta có:
(chọn) hoặc n = 5 (loại).
Khi đó, xác suất của biến cố “Lấy được 2 quả bóng có cùng màu” là
.
Vậy xác suất của biến cố “Lấy được 2 quả bóng có cùng màu” là 0,5.
Câu 13:
21/07/2024Gieo ngẫu nhiên 3 con xúc xắc cân đối và đồng chất. Tính xác suất của biến cố A: “Tích số chấm xuất hiện trên mỗi con xúc xắc chia hết cho 15”.
 Xem đáp án
Xem đáp án
Gọi B là biến cố “Tích số chấm xuất hiện trên mỗi con xúc xắc không chia hết cho 5”, C là biến cố “Tích số chấm xuất hiện trên mỗi con xúc xắc không chia hết cho 3”.
Khi đó A là biến cố đối của biến cố .
• Các số chấm không chia hết cho 5 là 1, 2, 3, 4, 6 nên .
• Các số chấm không chia hết cho 3 là 1, 2, 4, 5 nên .
• Các số chấm không chia hết cho 3 và 5 là 1, 2, 4 nên
.
Ta có
.
Do đó xác suất của biến cố A là
.
Câu 14:
21/07/2024Một hộp chứa 40 tấm thẻ cùng loại được đánh số lần lượt từ 1 đến 40. Lấy ra ngẫu nhiên đồng thời hai thẻ từ hộp. Tính xác suất của các biến cố:
a) “Tổng các số ghi trên 2 thẻ lấy ra nhỏ hơn 4 hoặc lớn hơn 76”;
 Xem đáp án
Xem đáp án
a) Gọi A là biến cố “Tổng các số ghi trên 2 thẻ lấy ra nhỏ hơn 4 hoặc lớn hơn 76”. A1 là biến cố “Tổng các số ghi trên 2 thẻ lấy ra nhỏ hơn 4” và A2 là biến cố “Tổng các số ghi trên 2 thẻ lấy ra lớn hơn 76”.
Khi đó .
Không gian mẫu của phép thử là .
Biến cố A1 xảy ra khi 2 tấm thẻ được chọn ghi số 1 và 2. Do đó số trường hợp xảy ra của biến cố A1 là 1. Từ đó
.
Biến cố A2 xảy ra khi 2 tấm thẻ được chọn ghi số 37 và 40; 38 và 40; 39 và 40; 38 và 39. Do đó số trường hợp xảy ra của biến cố A2 là 4. Từ đó
.
Do A1 và A2 là hai biến cố xung khắc nên
.
Câu 15:
21/07/2024b) “Tích các số ghi trên 2 thẻ lấy ra chia hết cho 10”.
 Xem đáp án
Xem đáp án
b) Gọi B là biến cố “Tích các số ghi trên 2 thẻ lấy ra chia hết cho 10”, B1 là biến cố “Tích các số ghi trên 2 thẻ lấy ra không chia hết cho 5” và B2 là biến cố “Tích các số ghi trên 2 thẻ lấy ra không chia hết cho 2”.
Khi đó B là biến cố đối của .
Từ 1 đến 40 có 8 số chia hết cho 5 và 32 số không chia hết cho 5 nên
.
Từ 1 đến 40 có 20 số chia hết cho 2 và 20 số không chia hết cho 2 nên
.
Từ 1 đến 40 có 4 số chia hết cho 10 nên số các số không chia hết cho 2 và 5 là số. Từ đó ta có
.
Ta có
.
Vậy xác suất của biến cố B “Tích các số ghi trên 2 thẻ lấy ra chia hết cho 10” là
.
