Giải SBT Toán 11 Cánh diều Bài 1. Đường thẳng và mặt phẳng trong không gian
Giải SBT Toán 11 Cánh diều Bài 1. Đường thẳng và mặt phẳng trong không gian
-
55 lượt thi
-
9 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
05/07/2024Cho hình chóp tứ giác S.ABCD có ABCD là hình bình hành. Điểm M thuộc cạnh SC. Trong các mặt phẳng sau, điểm M nằm trên mặt phẳng nào?
A. (ABCD).
B. (SAC).
C. (SAB).
D. (SAD).
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
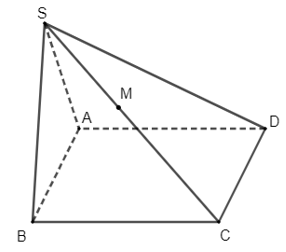
Vì M ∈ SC, mà SC ⊂ (SAC) nên M ∈ (SAC).
Câu 2:
21/07/2024Cho hình tứ diện ABCD. Giao tuyến của hai mặt phẳng (ABC) và (CDA) là đường thẳng:
A. AB.
B. BD.
C. CD.
D. AC.
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
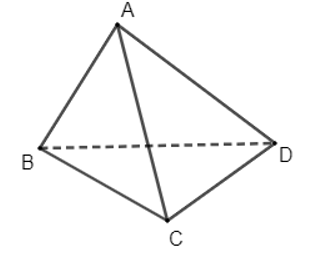
Vì A ∈ (ABC) và A ∈ (CDA) nên A là điểm chung thứ nhất của hai mặt phẳng (ABC) và (CDA).
Vì C ∈ (ABC) và C ∈ (CDA) nên C là điểm chung thứ hai của hai mặt phẳng (ABC) và (CDA).
Vậy đường thẳng AC là giao tuyến của hai mặt phẳng (ABC) và (CDA).
Câu 3:
20/07/2024Một đồ vật trang trí có bốn mặt phân biệt là các tam giác (Hình 7). Vẽ hình biểu diễn của đồ vật đó.
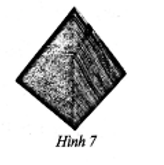
 Xem đáp án
Xem đáp án
Hình biểu diễn của đồ vật là:
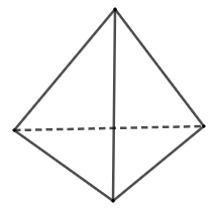
Câu 4:
11/07/2024Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB, BC. Chứng minh rằng bốn điểm M, N, C, D không cùng nằm trong một mặt phẳng.
 Xem đáp án
Xem đáp án
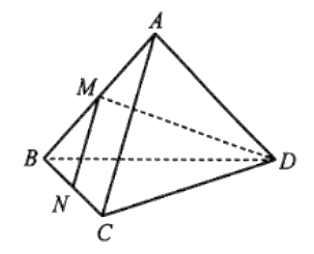
Giả sử bốn điểm M, N, C, D cùng thuộc một mặt phẳng.
Khi đó, M ∈ (NCD) nên M ∈ (BCD).
Như vậy, BM ⊂ (BCD), mà M ∈ AB nên A ∈ (BCD). Mâu thuẫn với giả thiết ABCD là tứ diện.
Vậy bốn điểm M, N, C, D không cùng nằm trong một mặt phẳng.
Câu 5:
18/07/2024Cho hai mặt phẳng (P), (Q) cắt nhau theo giao tuyến d và hai đường thẳng a, b lần lượt nằm trong (P), (Q). Chứng minh rằng nếu hai đường thẳng a, b cắt nhau thì giao điểm của chúng thuộc đường thẳng d.
 Xem đáp án
Xem đáp án

Gọi I là giao điểm của a và b. Khi đó, I vừa thuộc (P) vừa thuộc (Q). Suy ra I thuộc giao tuyến của hai mặt phẳng (P) và (Q). Vậy I thuộc d.
Câu 6:
19/07/2024Cho tứ diện ABCD. Trên các cạnh AC, CD lần lượt lấy các điểm E, F sao cho CE = 3EA, DF = 2FC.
a) Xác định giao tuyến của mặt phẳng (BEF) với các mặt phẳng (ABC), (ACD), (BCD).
b) Xác định giao điểm K của đường thẳng AD với mặt phẳng (BEF).
c) Xác định giao tuyến của hai mặt phẳng (BEF) và (ABD).
 Xem đáp án
Xem đáp án
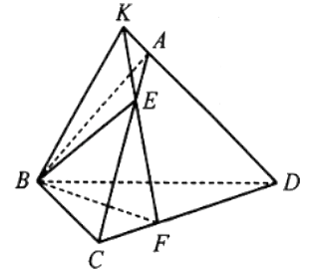
a) Vì E ∈ AC mà AC ⊂ (ABC) nên E ∈ (ABC) và E ∈ (BEF) nên E ∈ (ABC) ∩ (BEF).
Lại có B ∈ (BEF), B ∈ (ABC) nên B ∈ (BEF) ∩ (ABC).
Do vậy, BE = (BEF) ∩ (ABC).
Tương tự ta có EF = (BEF) ∩ (ACD) và BF = (BEF) ∩ (BCD).
b) Trong mặt phẳng (ACD), lấy K là giao điểm của AD và EF.
Khi đó, K ∈ (BEF). Suy ra K là giao điểm của AD và (BEF).
c) Vì K ∈ AD và AD ⊂ (ABD) nên K ∈ (ABD).
Theo câu b) ta có K ∈ (BEF).
Do đó, hai mặt phẳng (BEF) và (ABD) có hai điểm chung là B và K.
Câu 7:
20/07/2024Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N, P lần lượt là trung điểm của các cạnh SA, BC, CD.
a) Xác định giao điểm của đường thẳng NP với mặt phẳng (SAB).
b) Xác định giao tuyến của mặt phẳng (MNP) với các mặt phẳng (SAB), (SAD), (SBC), (SCD).
 Xem đáp án
Xem đáp án
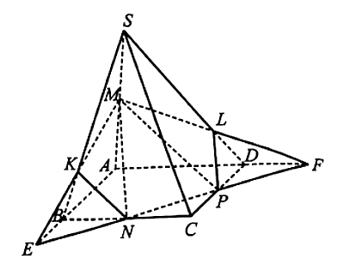
a) Vì N ∈ BC và P ∈ CD nên NP ⊂ (ABCD).
Trong mặt phẳng (ABCD), gọi E là giao điểm của NP và AB.
Ta có E thuộc AB nên E nằm trên mặt phẳng (SAB).
Vậy E là giao điểm của đường thẳng NP với mặt phẳng (SAB).
b)
+ Theo câu a) ta có E là một điểm chung của hai mặt phẳng (MNP) và (SAB).
Lại có M ∈ SA nên M ∈ (SAB) và M ∈ (MNP) nên M là điểm chung của hai mặt phẳng (MNP) và (SAB).
Do đó, giao tuyến của mặt phẳng (MNP) với mặt phẳng (SAB) là đường thẳng ME.
+ Trong mặt phẳng (ABCD), gọi F là giao điểm của NP và AD nên F là một điểm chung của mặt phẳng (MNP) với mặt phẳng (SAD).
Lại có M ∈ SA nên M ∈ (SAD) và M ∈ (MNP) nên M là một điểm chung của mặt phẳng (MNP) với mặt phẳng (SAD).
Khi đó, giao tuyến của mặt phẳng (MNP) với mặt phẳng (SAD) là đường thẳng MF.
+ Trong mặt phẳng (SAB), gọi K là giao điểm của ME và SB; trong mặt phẳng (SAD), gọi L là giao điểm của MF và SD. Khi đó, giao tuyến của mặt phẳng (MNP) với các mặt phẳng (SBC), (SCD) lần lượt là các đường thẳng NK và PL.
Câu 8:
11/07/2024Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N, P lần lượt là trung điểm của các cạnh SA, SB, SC.
a) Xác định giao điểm I của đường thẳng MP với mặt phẳng (SBD).
b) Xác định giao điểm Q của đường thẳng SD với mặt phẳng (MNP).
 Xem đáp án
Xem đáp án
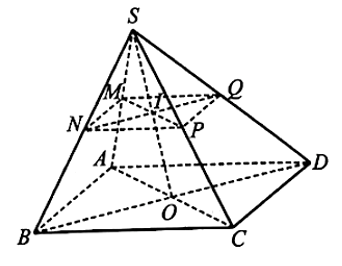
a) Trong mặt phẳng (ABCD), gọi O là giao điểm của AC và BD.
Vì O thuộc AC nên O thuộc (SAC). Vì M thuộc SA và P thuộc SC nên MP ⊂ (SAC).
Trong mặt phẳng (SAC), gọi I là giao điểm của MP và SO.
Vì I ∈ SO, mà O ∈ BD nên SO ⊂ (SBD), do đó I ∈ (SBD).
Vậy I là giao điểm của MP với mặt phẳng (SBD).
b) Trong mặt phẳng (SBD), gọi Q là giao điểm của NI và SD.
Vì Q ∈ NI nên Q ∈ (MNP).
Vậy Q là giao điểm của SD với mặt phẳng (MNP).
Câu 9:
23/07/2024Cho hình chóp tứ giác S.ABCD có đáy không là hình thang. Gọi O là giao điểm của AC và BD. Trên SO lấy điểm I sao cho SI = 2IO.
a) Xác định các giao điểm M, N lần lượt của SA, SD với mặt phẳng (IBC).
b*) Chứng minh rằng các đường thẳng AD, BC và MN đồng quy.
 Xem đáp án
Xem đáp án
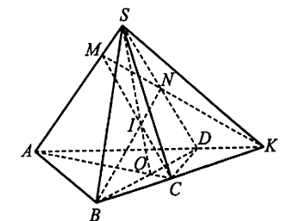
a) Trong mặt phẳng (SAC), gọi M là giao điểm của CI và SA.
Vì M ∈ CI nên M ∈ (IBC).
Vậy M là giao điểm của SA với mặt phẳng (IBC).
Tương tự, trong mặt phẳng (SBD), gọi N là giao điểm của BI với SD, khi đó, N là giao điểm của SD với mặt phẳng (IBC).
b*) Theo câu a) ta có M ∈ (IBC) và N ∈ (IBC) nên MN ⊂ (IBC).
Mà M ∈ SA ⊂ (SAD), N ∈ SD ⊂ (SAD) nên MN ⊂ (SAD).
Do đó, MN = (IBC) ∩ (SAD).
Vì ABCD không là hình thang nên AD cắt BC tại K.
Lại có K ∈ BC ⊂ (IBC), K ∈ AD ⊂ (SAD) nên K là một điểm chung của (IBC) và (SAD).
Do vậy K ∈ MN.
Vậy các đường thẳng AD, BC và MN cùng đi qua điểm K hay các đường thẳng AD, BC và MN đồng quy.
