Giải SBT Lí 10 Bài 16: Chuyển động tròn có đáp án
Giải SBT Lí 10 Bài 16: Chuyển động tròn có đáp án
-
105 lượt thi
-
11 câu hỏi
-
40 phút
Danh sách câu hỏi
Câu 1:
23/07/2024Phát biểu nào sau đây sai khi nói về một vật chuyển động tròn đều?
A. Quỹ đạo chuyển động là một đường tròn hoặc một phần của đường tròn.
B. Tốc độ của vật không đổi theo thời gian.
C. Với tốc độ xác định, bán kính quỹ đạo càng nhỏ thì phương của vận tốc biến đổi càng nhanh.
D. Với bán kính quỹ đạo xác định, nếu tốc độ tăng gấp đôi thì gia tốc hướng tâm cũng tăng gấp đôi.
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: D
D – sai vì bán kính tăng gấp đôi thì gia tốc hướng tâm tăng 4 lần.
Câu 2:
23/07/2024Một bánh xe đang quay đều, mỗi phút nó quay được
3000 vòng. Phát biểu nào sau đây sai khi nói về chuyển động của bánh xe?
A. Độ dịch chuyển góc của một điểm bất kì trên bánh xe (trừ những điểm thuộc trục quay) trong khoảng thời gian 0,01 giây bằng π radian.
B. Những điểm cách trục quay 10,0 cm thì có tốc độ 10π m/s.
C. Hai điểm bất kì trên bánh xe nếu cách nhau 20,0 cm thì có tốc độ hơn kém nhau một lượng 20π m/s.
D. Những điểm càng xa trục quay thì gia tốc hướng tâm càng lớn.
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: C
A – đúng vì tốc độ góc: 3000 vòng/ phút = 3000.2π60=100π(rad/s)
Hay trong khoảng thời gian 0,01 giây thì độ dịch chuyển góc của một điểm bất kì trên bánh xe bằng π radian.
B – đúng vì v=ωr=100π.0,1=10π(m/s)
C – sai vì chỉ những điểm nằm trên cùng một đường thẳng nối từ tâm quỹ đạo ra mới có tốc độ hơn kém nhau 20π m/s.
D – đúng vì gia tốc hướng tâm a=v2r tỉ lệ nghịch với bán kính quỹ đạo.
Câu 3:
23/07/2024Biết kim phút của đồng hồ treo tường có chiều dài a = 10,0 cm.
Tính độ dịch chuyển góc và quãng đường đi của điểm đầu kim phút trong khoảng thời gian t = 15,0 phút.
 Xem đáp án
Xem đáp án
Lời giải
Độ dịch chuyển góc của kim phút là:
θ=2π×tT=(2πrad)×15phut60phut=π2rad
Quãng đường đi của điểm đầu kim phút là:
s=θr=(π2rad)(10,0cm)≈15,7cm
Câu 4:
23/07/2024 Xem đáp án
Xem đáp án
Lời giải
Gọi tốc độ, tốc độ góc và chiều dài của kim phút và kim giờ lần lượt là v1,v2,ω1,ω2,r1,r2 theo giả thiết ta có:
v1v2=ω1r1ω2r2=15
Mà ω1ω2=2πT12πT2=T2T1=121=12 vậy r1r2=v1ω1v2ω2=1512
⇒r2=1215r1=1215.10=8cm
Câu 5:
23/07/2024Một người xách một xô có nước và vung tay làm xô nước quay trong mặt phẳng thẳng đứng, theo một vòng tròn đường kính 1,8 m. Biết khối lượng xô và nước là 5,4 kg.
Tính tốc độ nhỏ nhất mà xô nước phải được quay để khi ở đỉnh hình tròn, đáy xô quay lên trên, miệng hướng xuống dưới mà nước vẫn ở trong xô.
Câu 6:
23/07/2024 Xem đáp án
Xem đáp án
Lời giải
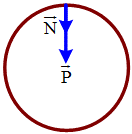
Theo định luật II Newton ta có:
\vec P + \,\vec N = m.\vec a
Chọn chiều dương chiếu vào tâm ta có:
N – P = m.aht
\Rightarrow N = m.aht + P
Theo định luật III Newton lực tác dụng lên tay người đó có độ lớn bằng lực do tay người đó tác dụng lên xô nước: F = N = m.aht + P = m(g + \frac{{{v^2}}}{r})
Mà theo ý a, có: v = \sqrt {gr}
\Rightarrow F = 2mg = 2\left( {5,4kg} \right)\left( {9,81\frac{m}{{{s^2}}}} \right) = 105,9N \approx 106N
Câu 7:
23/07/2024 Xem đáp án
Xem đáp án
Lời giải
Tốc độ góc trong chuyển động quay của Trái Đất là:
\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{24\left( {3600s} \right)}} = \frac{\pi }{{43200}}rad/s
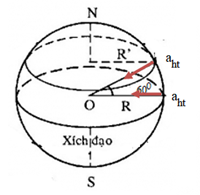
Gia tốc hướng tâm của người đứng ở xích đạo là:
{a_1} = {\omega ^2}R = {\left( {\frac{\pi }{{43200}}rad/s} \right)^2}\left( {6400000m} \right) \approx 0,034m/{s^2}
Gia tốc hướng tâm của người ở vĩ tuyến 600 là:
{a_2} = {\omega ^2}R\cos 60^\circ = {\left( {\frac{\pi }{{43200}}rad/s} \right)^2}\left( {6400000m} \right)\frac{1}{2} \approx 0,017m/{s^2}
Câu 8:
23/07/2024Ở hình 1.10b trang 112 sách giáo khoa Vật lí 10, viên đá có khối lượng 200g, bán kính vòng quay là 40 cm. Sợi dây hợp với phương thẳng đứng góc 560.
Tìm lực căng dây.
 Xem đáp án
Xem đáp án
Lời giải
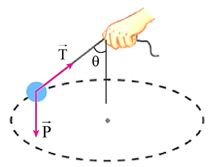
Dựa vào hình vẽ ta xác định được: T\cos \theta = mg
\Rightarrow T = \frac{{\left( {0,200kg} \right)\left( {9,81\frac{m}{{{s^2}}}} \right)}}{{\cos 56^\circ }} = 3,5N
Câu 9:
23/07/2024 Xem đáp án
Xem đáp án
Lời giải
{F_{ht}} = T\sin \theta = \left( {3,5N} \right)\sin 56^\circ = 2,9N
F = m{\omega ^2}r \Rightarrow {\omega ^2} = \frac{{2,9}}{{0,200 \times 0,40}} = 36,25
\Rightarrow \omega \approx 6,0rad{s^{ - 1}}
Câu 10:
23/07/2024Ở một sân tập phẳng, rộng người lái xe đua phải thực hiện vòng chạy trên một đường tròn bán kính R = 121 m. Biết hệ số ma sát nghỉ cực đại giữa xe và mặt sân là 0,9.
Lấy g = 10,0 m/s2. Tốc độ lớn nhất mà xe có thể chạy là bao nhiêu để không bị trượt?
 Xem đáp án
Xem đáp án
Lời giải
Tốc độ cho phép ô tô để nó không bị trượt trên mặt sân phải thỏa mãn điều kiện:
\Rightarrow \frac{{m{v^2}}}{R} \le \mu mg
\Rightarrow v \le \sqrt {\mu gR} = \sqrt {0,90\left( {10,0m/{s^2}} \right)\left( {121m} \right)} = 33m/s
Vậy tốc độ lớn nhất là 33 m/s.
Câu 11:
23/07/2024 Xem đáp án
Xem đáp án
Lời giải
Một trong số những giải pháp dễ thực hiện đối với người lái xe đó là tăng tốc (từ dưới chân cầu) đến vận tốc cần thiết và điều khiển xe chuyển động tròn đều qua cầu với vận tốc v.
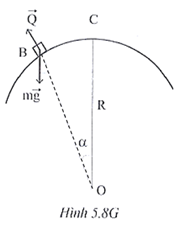
Khi xe chuyển động tròn đều trên cầu, theo định luật II Newton tại mọi vị trí ta luôn có: m\overrightarrow g + \overrightarrow Q = m\overrightarrow a
Chọn chiều dương (+) hướng vào tâm:
mg\cos \alpha - Q = m\frac{{{v^2}}}{R}
\Rightarrow Q = mg\cos \alpha - m\frac{{{v^2}}}{R}
Theo định luật III Newton thì áp lực xe tác dụng lên cầu có độ lớn là:
N = Q = mg\cos \alpha - m\frac{{{v^2}}}{R}
Vậy N lớn nhất khi α = 0 và giá trị đó không được vượt giới hạn áp lực cho phép của cầu.
Ta có: P - m\frac{{{v^2}}}{R} \le {N_{\max }}
\Rightarrow v \ge \sqrt {\frac{{P - {N_{\max }}}}{m}R} = \sqrt {\frac{{200000N - 60000N}}{{20000}}\left( {50,0m} \right)}
\Rightarrow v \approx 18,7m/s \approx 67,3km/h