Giải SBT Lí 10 Bài 12: Năng lượng và công có đáp án
-
103 lượt thi
-
22 câu hỏi
-
40 phút
Danh sách câu hỏi
Câu 1:
17/07/2024Một người tác dụng một lực có độ lớn không đổi F lên một vật. Trong khoảng thời gian chịu tác dụng của lực F vật đó bị dời chỗ so với vị trí ban đầu một đoạn thẳng có độ dài s. Nhận xét nào sau đây là chính xác nhất?
A. Người đó đã thực hiện một công A = Fs lên vật.
B. Người đó nhận công A’ = Fs từ vật.
C. Công mà người đó thực hiện lên vật có giá trị cực đại là Am = Fs.
D. Công của lực F không thể mang dấu âm.
Xem đáp án
Lời giải
Đáp án đúng là: C
Ta có biểu thức tính công: A = Fscos α ≤ Fs
Câu 2:
19/07/2024Nhận xét nào sau đây là đúng về công?
A. Công là đại lượng vô hướng.
B. Giá trị của công không phụ thuộc vào người quan sát.
C. Công là đại lượng có hướng.
D. Công là đại lượng vô hướng và luôn dương.
Xem đáp án
Lời giải
Đáp án đúng là: A
Công là đại lượng vô hướng, có thể dương, âm hoặc bằng không.
Câu 3:
21/07/2024 Xem đáp án
Lời giải
Công của người thực hiện:
\[A \ge mgh = 20,0kg \times 9,8m/{s^2} \times 1,2m = 235,2J\]
Nếu coi người thực hiện nâng vật, làm cho vật chuyển động đều thì công có độ lớn bằng 235,2 J.
Câu 4:
21/07/2024 Xem đáp án
Lời giải
Năng lượng điện mà lò sưởi đã sử dụng:
\[W = A = {\rm{P}}.t = 2,5.4 = 10\,kWh = {36.10^6}\,J\]
Câu 5:
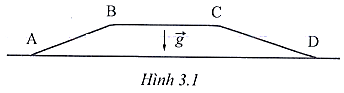
17/07/2024Một ô tô có khối lượng m = 1,30.103 kg di chuyển trên đoạn đường ABCD có dạng như hình 3.1, trong đó BC là đoạn đường nằm ngang ở độ cao h = 50,0 m so với mặt phẳng nằm ngang chứa AD. Biết rằng BC = 20 km, gia tốc rơi tự do g = 9,80 m/s2, độ dài các cung cong nối các đoạn đường thẳng với nhau rất nhỏ so với chiều dài của các đoạn thẳng đó, hãy tính công của trọng lực trên các đoạn đường AB, BC, CD.
Xem đáp án
Lời giải
Công của trọng lực trên các đoạn đường AB, BC và CD
\[{A_{AB}} = - mgh = - {1,3.10^3}.9,8.50 = - 637kJ\]
\[{A_{BC}} = 0\]
\[{A_{CD}} = mgh = {1,3.10^3}.9,8.50 = 637kJ\]
Câu 6:
20/07/2024Một chiếc xe khối lượng m = 10,0 tấn, chuyển động trên mặt đường nằm ngang với vận tốc không đổi v = 40,0 km/h. Biết gia tốc rơi tự do là g = 9,80 m/s2.
Tính lực mà mặt đường tác dụng lên xe.
Xem đáp án
Lời giải
Vì xe chuyển động với vận tốc không đổi nên lực mà mặt đường tác dụng lên xe cân bằng với trọng lượng của xe, có chiều hướng thẳng đứng lên trên và độ lớn bằng:
F = mg = 10000 . 9,8 = 98 kN
Câu 7:
20/07/2024 Xem đáp án
Câu 8:
21/07/2024 Xem đáp án
Lời giải
Công của trọng lực: \[{A_p} = mgh = {65,5.10^{ - 6}}.9,8.10 = {6,42.10^{ - 3}}\,J\]
Vì giọt nước mưa chuyển động thẳng đều nên theo định luật III Newton, ta có lực cản cân bằng với trọng lượng của vật. Công của lực cản
\[{A_C} = - {F_C}h = - mgh = - {6,42.10^{ - 3}}\,J\]
Câu 9:
17/07/2024Một người dùng lực F hợp với phương nằm ngang một góc \[\alpha = 60,0^\circ \], để kéo vật có khối lượng m = 50,0 kg trượt trên mặt sàn nằm ngang một đoạn thẳng có độ dài s = 10,0 m với tốc độ không đổi. Biết hệ số ma sát giữa vật và mặt sàn là \[\mu = 0,250\]; thành phần thẳng đứng của lực F hướng từ dưới lên trên, gia tốc rơi tự do
g = 9,8 m/s2. Tính:
Công của trọng lực.
Xem đáp án
Lời giải
Công của trọng lực: Ap = 0
Câu 10:
17/07/2024 Xem đáp án
Lời giải
Giản đồ vecto
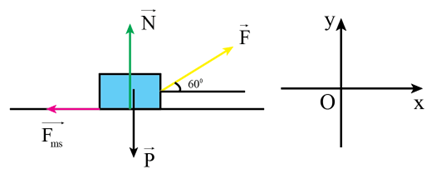
Từ định luật II Newton: \[\overrightarrow F + \overrightarrow P + \overrightarrow N + \overrightarrow {{F_{ms}}} = \overrightarrow 0 \] (do vật chuyển động đều)
Vì vật chuyển động thẳng đều nên độ lớn của lực ma sát bằng độ lớn của thành phần nằm ngang của lực F.
Theo phương Ox: \[F\cos \alpha - {F_{ms}} = 0 \Leftrightarrow F\cos \alpha - \mu N = 0\]
Theo phương Oy: \[N + F\sin \alpha = P \Rightarrow N = mg - F\sin \alpha \]
\[ \Rightarrow \mu \left( {mg - F\sin \alpha } \right) = F\cos \alpha \]
\[ \Rightarrow F = \frac{{\mu mg}}{{\cos \alpha + \mu \sin \alpha }}\]
Công của lực F:
\[{A_F} = Fs\cos \alpha = \frac{{\mu mgs\cos \alpha }}{{\cos \alpha + \mu \sin \alpha }} \approx 855J\]
Câu 11:
17/07/2024 Xem đáp án
Lời giải
Lực ma sát: \[{F_{ms}} = \mu N = \mu \left( {mg - F\sin \alpha } \right)\]
Công của lực ma sát
\[{A_{ms}} = - \mu \left( {mg - F\sin \alpha } \right)s = - \frac{{\mu mgs\cos \alpha }}{{\cos \alpha + \mu \sin \alpha }} \approx - 855J\]
Câu 12:
18/07/2024Một người dùng lực F hợp với phương nằm ngang một góc \[\alpha = 30,0^\circ \], để đẩy vật có khối lượng m = 50,0 kg trượt trên mặt sàn nằm ngang một đoạn thẳng có độ dài s = 15,0 m với vận tốc không đổi. Biết hệ số ma sát giữa vật và mặt sàn là \[\mu = 0,30\]; thành phần thẳng đứng của lực F hướng từ trên xuống dưới, gia tốc rơi tự do g = 9,80 m/s2. Tính
Công của trọng lực.
Xem đáp án
Lời giải
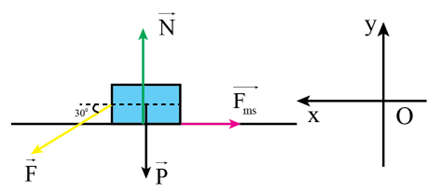
Công của trọng lực AP = 0
Câu 13:
17/07/2024 Xem đáp án
Lời giải
Từ định luật II Newton: \[\overrightarrow F + \overrightarrow P + \overrightarrow N + \overrightarrow {{F_{ms}}} = \overrightarrow 0 \] (do vật chuyển động đều)
Theo phương Ox: \[F\cos \alpha - {F_{ms}} = 0 \Leftrightarrow F\cos \alpha = \mu N\]
Theo phương Oy: \[N = F\sin \alpha + P \Rightarrow N = mg + F\sin \alpha \]
Vì vật chuyển động thẳng đều nên độ lớn của lực ma sát bằng độ lớn của thành phần nằm ngang của lực F.
\[\mu \left( {mg + F\sin \alpha } \right) = F\cos \alpha \]
\[ \Rightarrow F = \frac{{\mu mg}}{{\cos \alpha - \mu \sin \alpha }} = \frac{{0,3.50.9,8}}{{cos{{30}^0} - 0,3.\sin {{30}^0}}} \approx 205(N)\]
Công của lực F là
\[A = Fs\cos \alpha = 205.15.c{\rm{os3}}{{\rm{0}}^0} \approx 2663J\]
Câu 14:
17/07/2024 Xem đáp án
Lời giải
Công của lực ma sát là
\[{A_{ms}} = - \mu \left( {mg + F\sin \alpha } \right)s = - 0,3(50.9,8 + 205.\sin {30^0}).15 \approx - 2666,25J\]
Câu 15:
23/07/2024Một ô tô có khối lượng m = 3,50 tấn đi hết một con dốc có chiều dài s = 100 m trong khoảng thời gian \[\tau = 10,0s\] với tốc độ không đổi. Biết rằng con dốc là một đoạn đường thẳng hợp với mặt phẳng nằm ngang một góc \[\alpha = 30,0^\circ \] và gia tốc rơi tự do là g = 9,80 m/s2. Tính công và công suất của trọng lực trong các trường hợp.
Ô tô đi lên dốc.
Xem đáp án
Lời giải
Công và công suất của trọng lực khi ô tô lên dốc:
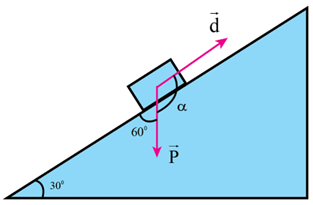
\[{A_1} = P.s.\cos \alpha = mg.s.\cos \left( {{{180}^0} - {{60}^0}} \right)\]
\( \Rightarrow {A_1} = 3,5.1000.9,8.100.cos{120^0} = - 1715000J\)
Công suất của trọng lực trong trường hợp này là
\[{{\rm{P}}_1} = \frac{{{A_1}}}{\tau } = \frac{{ - 1715000}}{{10}} \approx - 171500W\]
Câu 16:
21/07/2024Tính công và công suất của trọng lực trong các trường hợp.
Xem đáp án
Lời giải
Công và công suất của trọng lực khi ô tô xuống dốc
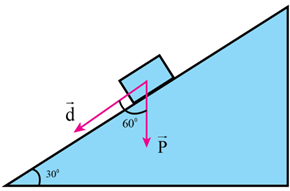
\[{A_2} = P.s.\cos \alpha = mg.s.\cos {60^0}\]
\( \Rightarrow {A_2} = 3500.9,8.100.cos{60^0} = 1715000J\)
Công suất của trọng lực trong trường hợp này là
\[{{\rm{P}}_2} = \frac{{{A_2}}}{\tau } = \frac{{1715000}}{{10}} \approx 171500W\]
Câu 17:
21/07/2024Một vật có khối lượng m = 300 g được ném lên từ mặt đất với tốc độ ban đầu v0 = 19,6 m/s theo hướng hợp với mặt đất nằm ngang một góc \[\alpha = 30,0^\circ \]. Bỏ qua lực cản của không khí, gia tốc rơi tự do g = 9,80 m/s2. Tính công suất của trọng lực thực hiện lên vật.
tại thời điểm t = 0.
Xem đáp án
Lời giải
Công suất của trọng lực
\[{{\rm{P}}_g} = P.v = - mg{v_y} = - mg\left( {{v_0}\sin \alpha - gt} \right)\]
Công suất của trọng lực thực hiện lên vật tại thời điểm t = 0
\[{{\rm{P}}_g} = - mg{v_0}\sin \alpha = - 0,3.9,8.19,6.\sin {30^0} = - 28,8W\]
Câu 18:
17/07/2024Tính công suất của trọng lực thực hiện lên vật.
tại thời điểm vật đạt độ cao cực đại.
Xem đáp án
Lời giải
Khi vật đạt độ cao cực đại, vy = 0 nên công suất của trọng lực thực hiện lên vật là
\[{{\rm{P}}_{g{h_{\max }}}} = 0\]
Câu 19:
18/07/2024Tính công suất của trọng lực thực hiện lên vật.
Xem đáp án
Lời giải
Độ cao của vật tại thời điểm t
\[y = {v_0}\left( {\sin \alpha } \right)t - \frac{1}{2}g{t^2}\]
Vật chạm đất khi \[t = \frac{{2{v_0}\sin \alpha }}{g}\], lúc đó công suất của trọng lực tác dụng lên vật là
\[{{\rm{P}}_g} = mg{v_0}\sin \alpha = 0,3.9,8.19,6.\sin {30^0} = 28,8W\]
Câu 20:
17/07/2024Để múc nước từ dưới giếng lên bể người ta dùng một chiếc gầu có khối lượng m0 = 500 g. Để di chuyển ổn định (nước trong gầu không bị thất thoát ra ngoài trong quá trình kéo nước từ giếng lên bể) gầu đựng được một lượng nước có khối lượng tối đa m = 4,50 kg. Biết rằng khối lượng của dây gầu không đáng kể, mặt nước trong giếng cách mặt bể một khoảng h = 5,00 m, gia tốc rơi tự do g = 9,80 m/s2. Trong các quá trình dùng gầu để đưa nước từ giếng lên bể.
Tính công toàn phần tối thiểu để đưa được M = 9,00 kg nước từ giếng lên bể.
Xem đáp án
Lời giải
Mỗi lần múc được m = 4,5 kg nước, số lượng nước cần múc là M = 9kg.
Số lần tối thiểu cần múc: \[k = \frac{M}{m} = \frac{9}{{4,5}} = 2\]
Công tối thiểu cho 1 lần múc:
\[A = \left( {m + {m_0}} \right)gh = \left( {4,5 + 0,5} \right).9,8.5 = 245J\]
Công toàn phần: \[{A_{tp}} = k.A = 490J\]
Câu 21:
22/07/2024 Xem đáp án
Lời giải
Giả sử mỗi lần chỉ múc được mn kg nước (do có sự thất thoát ra ngoài)
Công có ích: \[{A_{ci}} = {m_n}gh\] (công có ích múc được mn kg nước)
Công toàn phần: \[{A_{tp}} = \left( {m + {m_n}} \right)gh\]
Hiệu suất của quá trình múc nước
\[H = \frac{{{m_n}gh}}{{\left( {{m_0} + {m_n}} \right)gh}} = \frac{1}{{1 + \frac{{{m_0}}}{{{m_n}}}}} \le \frac{1}{{1 + \frac{{{m_0}}}{m}}}\] (vì khối lượng nước múc được tối đa là m)
Hiệu suất cực đại của quá trình múc nước
\[{H_{\max }} = \frac{1}{{1 + \frac{{{m_0}}}{m}}} = \frac{1}{{1 + \frac{{0,5}}{{4,5}}}} = 90,0\% \]
Câu 22:
17/07/2024 Xem đáp án
Lời giải
Công toàn phần của quá trình múc nước với lực kéo F
\[{A_{{F_{tp}}}} = Fh = 60.5 = 300J\]
Hiệu suất của quá trình múc nước này:
\[H = \frac{{(m + {m_0})gh}}{{Fh}} = \frac{{(4,5 + 0,5).9,8.5}}{{60.5}} \approx 81,67\% \]