Giải SBT KHTN 7 CD Bài 13. Sự phản xạ ánh sáng có đáp án
Giải SBT KHTN 7 CD Bài 13. Sự phản xạ ánh sáng có đáp án
-
188 lượt thi
-
14 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
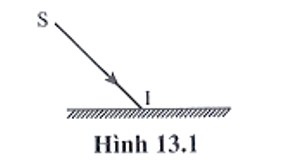
12/07/2024Trên hình 13.1 vẽ một tia sáng SI chiếu tới một gương phẳng. Góc tạo bởi tia SI với mặt gương bằng 450. Hãy vẽ tiếp tia phản xạ và tính góc phản xạ.
 Xem đáp án
Xem đáp án
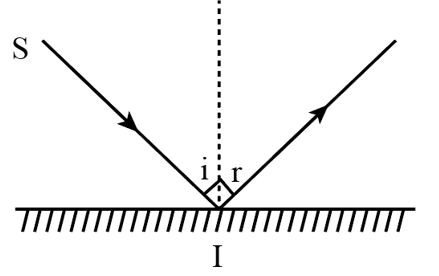
Theo định luật phản xạ ánh sáng:
Góc tới = góc phản xạ
Mà i = 900 – 450 = 450
Vậy góc phản xạ r = 450.
Câu 2:
08/07/2024Cho bóng đèn LED nhỏ (S) nằm trước gương phẳng. Hãy xác định vùng đặt mắt để có thể quan sát được ảnh của bóng đèn.
 Xem đáp án
Xem đáp án
Câu 3:
21/07/2024Chiếu một tia sáng đến một gương phẳng. Biết tia phản xạ và tia tới hợp với nhau một góc 600. Khi đó góc phản xạ có giá trị là
A. 150.
B. 300.
C. 450.
D. 600.
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
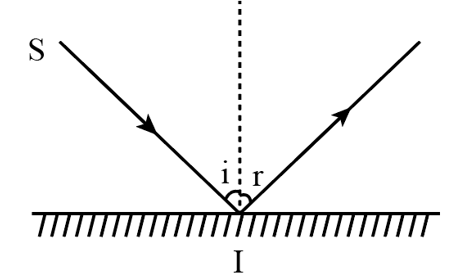
Theo định luật phản xạ ánh sáng:
góc phản xạ = góc tới
Câu 4:
11/07/2024Một tia sáng chiếu tới gương phẳng với góc tới là 300. Hình vẽ nào sau đây biểu diễn đúng sự phản xạ của tia sáng trên gương?
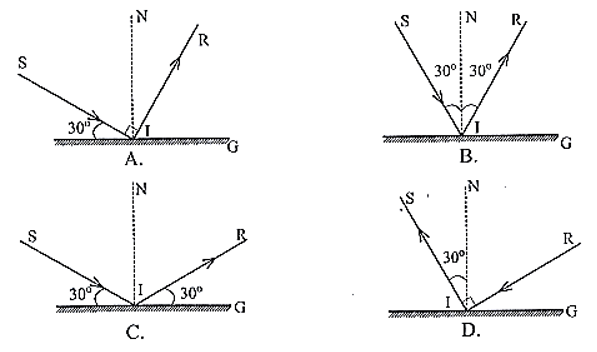
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Theo định luật phản xạ ánh sáng: góc tới = góc phản xạ nên chỉ có hình B thỏa mãn.
Câu 5:
22/07/2024Cho đường truyền tia sáng như hình 13.2. Góc phản xạ có giá trị nào sau đây?
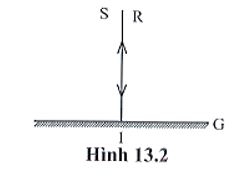
A. 00.
B. 900.
C. 1800.
D. Không xác định được.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Theo định luật phản xạ ánh sáng: góc phản xạ = góc tới = 00.
Câu 6:
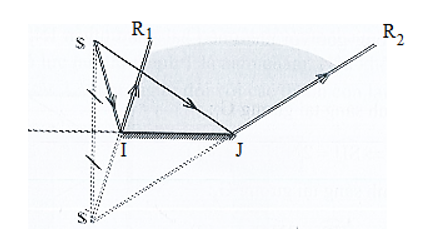
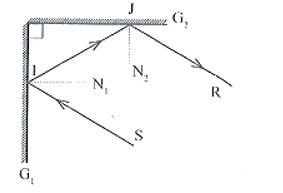
22/07/2024Hai gương phẳng G1 và G2 đặt song song với nhau, mặt phản xạ quay vào nhau. Tia tới SI được chiếu lên gương G1 phản xạ một lần trên gương G2 (hình 13.3.). Chứng minh tia tới SI song song với tia phản xạ cuối cùng trên gương G2.
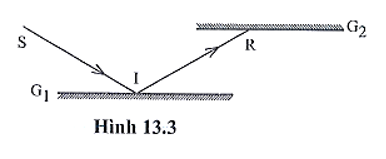
 Xem đáp án
Xem đáp án
Giả sử SI là tia tới, góc tới là
Theo định luật phản xạ ánh sáng, tại gương G1, ta có: (1)
Do hai gương đặt song song với nhau nên pháp tuyến IN ở gương G1 và pháp tuyến RN’ ở gương G2 song song với nhau, tia phản xạ ở G1 chính là tia tới ở gương G2:
Theo định luật phản xạ ánh sáng, tại gương G2, ta có: (2)
Từ (1) và (2) ta có:
Vì hai góc này ở vị trí so le trong nên SI song song với RK.
Câu 7:
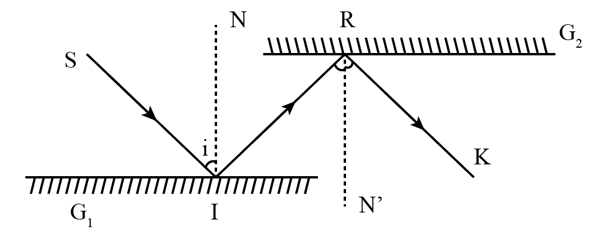
18/07/2024Hai gương G1 và G2 đặt vuông góc nhau, mặt phản xạ quay vào nhau. Tia tới SI được chiếu lên gương G1 (hình 13.4) lần lượt phản xạ trên gương G1 rồi trên gương G2. Chứng minh tia tới SI song song với tia phản xạ cuối cùng trên gương G2.
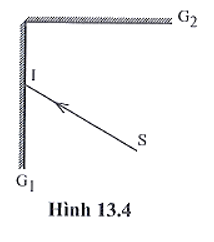
 Xem đáp án
Xem đáp án
Áp dụng định luật phản xạ ánh sáng tại gương G1, ta có:
(1)
Áp dụng định luật phản xạ ánh sáng tại gương G2, ta có:
(2)
Ta có, nên hai pháp tuyến
Câu 8:
04/07/2024Trong số các phát biểu sau đây, phát biểu nào đúng, phát biểu nào sai?
a) Ảnh của một vật tạo bởi gương phẳng là ảnh ảo.
b) Ảnh của vật tạo bởi gương phẳng hứng được trên màn ảnh.
c) Ảnh của vật tạo bởi gương phẳng có kích thước lớn hơn vật.
d) Khoảng cách từ ảnh tới gương bằng khoảng cách từ vật tới gương.
e) Ảnh của vật tạo bởi gương phẳng không hứng được trên màn ảnh.
 Xem đáp án
Xem đáp án
a) Đúng vì ảnh tạo bởi gương phẳng không hứng được trên màn chắn.
b) Sai vì ảnh tạo bởi gương phẳng là ảnh ảo.
c) Sai vì ảnh tạo bởi gương phẳng có kích thước bằng vật.
d) Đúng
e) Đúng
Câu 9:
15/07/2024Bằng hình vẽ hãy giải thích vì sao trong các tiệm cắt tóc người ta thường bố trí hai cái gương: Một cái treo trước mặt người cắt tóc và một cái treo hơi cao ở phía sau lưng ghế ngồi.
 Xem đáp án
Xem đáp án

Câu 10:
15/07/2024Mặt của miếng bìa ở hình 13.5 được đặt đối diện với mặt phẳng gương. Hình nào dưới đây là ảnh của miếng bìa trong gương?

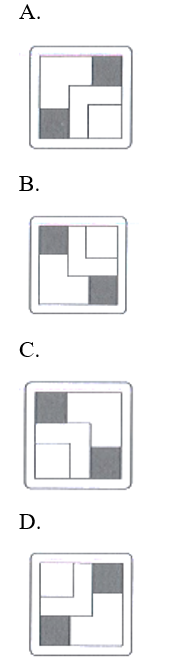
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
A, B, D không phải là ảnh của hình đã cho qua gương phẳng.
Câu 11:
18/07/2024Mặt của miếng bìa có hình cốc ở hình 13.6 được đặt đối diện với mặt phẳng gương. Hình nào dưới đây là ảnh của miếng bìa trong gương?
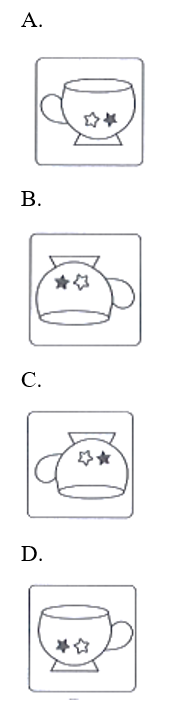
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
B, C, D không phải là ảnh của vật qua gương phẳng.
Câu 12:
15/07/2024Trò chơi “Đặt đúng, bắn trúng”
Cho các vật dụng sau:
- Hộp bìa catton có đục lỗ để đặt được đèn laser và vẽ một mục tiêu lên thành hộp.
- Một đèn laser nhỏ được đặt cố định trong hộp.
- 5 gương phẳng nhỏ.
- Băng dính hai mặt.
Dùng các vật dụng trên chế tạo bộ dụng cụ như hình 13.7.
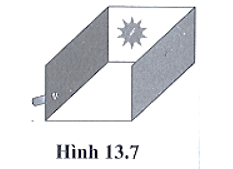
Cách chơi:
- Người chơi dự đoán vị trí đặt 5 gương trên thành hộp.
- Dán các tấm gương phẳng lên các vị trí đã đánh dấu.
- Ai đưa được vệt sáng của tia laser sau 5 lần phản xạ trên 5 gương gần mục tiêu nhất là người chiến thắng.
Lưu ý: Không để tia laser chiếu trực tiếp hoặc phản xạ vào mắt.
 Xem đáp án
Xem đáp án
Các em tự thực hiện theo hướng dẫn ở đề bài.
Câu 13:
17/07/2024Sự tạo ảnh qua hai gương
a) Khi đi tham quan nhà gương ở công viên, một bạn học sinh thấy một em bé ngồi trước hai gương phẳng ghép với nhau thì có rất nhiều ảnh trong gương (hình 13.8). Bạn học sinh đó thắc mắc, không biết số ảnh trong gương phụ thuộc vào yếu tố nào? Em hãy đưa ra câu trả lời dự đoán.

 Xem đáp án
Xem đáp án
a. Số ảnh trong gương phụ thuộc vào các yếu tố:
+ Số gương được ghép.
+ Cách ghép các gương (tức là tùy thuộc vào góc hợp bởi giữa các gương).
Câu 14:
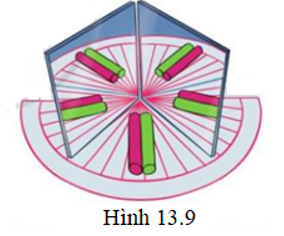
18/07/2024b) Thực hiện thí nghiệm
Dụng cụ
+ 2 gương phẳng nhỏ.
+ 1 thước chia độ bằng bìa.
+ 2 đoạn ống hút khoảng 4 cm.
Tiến hành
Đặt hai gương vuông góc với thước chia độ sao cho hai gương hợp với nhau một góc nhọn. Đặt ống hút trong góc tạo bởi hai gương (hình 13.9). Thay đổi góc giữa các gương và đếm số ảnh được tạo bởi hệ gương rồi ghi kết quả như bảng dưới đây.
|
Góc giữa hai gương |
|
30o |
40o |
50o |
60o |
70o |
80o |
90o |
|
Số ảnh (n) |
n |
|
|
|
|
|
|
|
Từ số liệu vừa thu được, em có thể dự đoán công thức liên hệ giữa và n không? Nếu có, em hãy ghi lại biểu thức đó.
 Xem đáp án
Xem đáp án
b. Tiến hành thí nghiệm thu được bảng số liệu sau:
|
Góc giữa hai gương |
|
30o |
40o |
50o |
60o |
70o |
80o |
90o |
|
Số ảnh (n) |
n |
11 |
8 |
6 |
5 |
4 |
3 |
3 |
Công thức liên hệ giữa và n có dạng: với
Chứng minh:
Chú ý: Mỗi gương phẳng sẽ tạo ra một mặt phẳng tới (do đường thẳng chứa gương tạo thành), có ảnh của vật qua gương khi vật nằm trong mặt phẳng tới. Nếu vật không nằm trong mặt phẳng tới sẽ không tạo ra ảnh.

Sơ đồ tạo ảnh qua hệ:
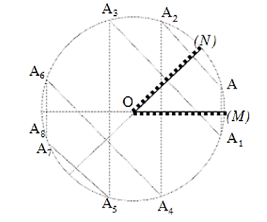
Từ bài toán ta có thể biểu diễn một số trường hợp đơn giản. Theo hình vẽ ta có:
….
Theo điều kiện bài toán thì
Vậy góc
Tức là ảnh A2k-1 và ảnh A2k trùng nhau.
Trong hai ảnh này có một ảnh sau gương (M) và một ảnh sau gương (N) nên không tiếp tục cho ảnh nữa.
Vậy số ảnh của A cho bởi hai gương là: n = 2k – 1 ảnh.
