Đề kiểm tra giữa học kì 2 Toán 10 Kết nối tri thức có đáp án
Đề kiểm tra giữa học kì 1 Toán 10 Kết nối tri thức có đáp án - Đề 1
-
434 lượt thi
-
38 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
16/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Câu 2:
16/07/2024Cho hàm số dưới dạng bảng như sau:
|
x |
1 |
2 |
3 |
4 |
5 |
|
y |
1 |
3 |
5 |
7 |
9 |
Giá trị của hàm số y tại x = 3 là
 Xem đáp án
Xem đáp án
Đáp án: C
Câu 3:
15/07/2024Cho hàm số y = f(x) có đồ thị như hình dưới.
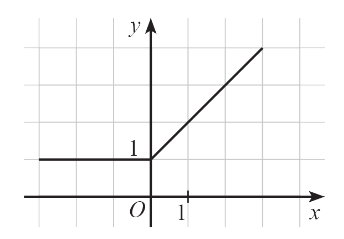
Hàm số trên đồng biến trên khoảng
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Từ hình vẽ ta thấy đồ thị hàm số y = f(x) đi lên từ trái sang phải trên khoảng (0; + ∞). Vậy hàm số này đồng biến trên khoảng (0; + ∞).
Câu 4:
17/07/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Biểu thức \(\frac{{x + 2}}{{{x^2} - 3x + 2}}\) có nghĩa khi x2 – 3x + 2 ≠ 0 ⇔ x ≠ 1 và x ≠ 2.
Vậy tập xác định của hàm số \(y = \frac{{x + 2}}{{{x^2} - 3x + 2}}\) là D = ℝ \ {1; 2}.
Câu 5:
17/07/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: \(y\left( {10} \right) = 2\sqrt {{{10}^2} - 5.10} = 10\sqrt 2 \).
Câu 6:
17/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Câu 7:
19/07/2024 Xem đáp án
Xem đáp án
Câu 9:
19/07/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có: \( - \frac{b}{{2a}} = - \frac{{ - 8}}{{2.2}} = 2\).
Vì hệ số a = 2 > 0 nên hàm số f(x) đồng biến trên khoảng (2; + ∞), nghịch biến trên khoảng (– ∞; 2).
Câu 10:
23/07/2024Xác định parabol y = ax2 + c, biết rằng parabol này đi qua hai điểm A(1; 1) và B(2; – 2).
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Vì parabol đi qua hai điểm A(1; 1) và B(2; – 2) nên suy ra \(\left\{ \begin{array}{l}a + c = 1\\4a + c = - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 1\\c = 2\end{array} \right.\).
Vậy parabol có phương trình là: y = – x2 + 2.Câu 12:
13/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Câu 13:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Câu 18:
17/07/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Bình phương hai vế của phương trình \(\sqrt {4 - 3{x^2}} = 2x - 1\) ta được
4 – 3x2 = 4x2 – 4x + 1.
Sau khi thu gọn ta được 7x2 – 4x – 3 = 0. Từ đó tìm được x = 1 hoặc \(x = - \frac{3}{7}\).
Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta thấy chỉ có x = 1 thỏa mãn.
Vậy phương trình đã cho có 1 nghiệm là x = 1.
Câu 19:
17/07/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Cách 1. Thay lần lượt các giá trị ở từng đáp án vào cho đến khi tìm được giá trị thỏa mãn.
Cách 2. Giải phương trình
Bình phương hai vế của phương trình \(\sqrt {3{x^2} - 6x + 1} = \sqrt {{x^2} - 3} \) ta được
3x2 – 6x + 1 = x2 – 3.
Rút gọn ta được x2 – 3x + 2 = 0. Từ đó ta tìm được x = 1 hoặc x = 2.
Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta thấy chỉ có x = 2 thỏa mãn.
Vậy phương trình đã cho có 1 nghiệm là x = 2.
Câu 20:
17/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Câu 22:
15/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Câu 23:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Câu 24:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Đường thẳng d: \(\left\{ \begin{array}{l}x = 5 + t\\y = - 9 - 2t\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t = x - 5\\y = - 9 - 2t\end{array} \right.\)⇒ y = – 9 – 2 . (x – 5) ⇔ 2x + y – 1 = 0.
Câu 25:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Bốn phương trình đã cho đều là dạng của phương trình đường thẳng.
Thay lần lượt toa độ của A, B vào từng phương trình ta thấy tọa độ của A và B đều thỏa mãn phương trình ở đáp án D.
Câu 26:
20/07/2024Trong mặt phẳng tọa độ, xét hai đường thẳng
∆1: a1x + b1y + c1 = 0; ∆2: a2x + b2y + c2 = 0.
và hệ phương trình: \[\left\{ \begin{array}{l}{a_1}x + {b_1}y + {c_1} = 0\\{a_2}x + {b_2}y + {c_2} = 0\end{array} \right.\] (*).
Khi đó, ∆1 song song với ∆2 khi và chỉ khi
 Xem đáp án
Xem đáp án
Đáp án: B
Câu 27:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Câu 28:
16/07/2024Trong mặt phẳng tọa độ, cho hai đường thẳng
∆1: a1x + b1y + c1 = 0; ∆2: a2x + b2y + c2 = 0,
với các vectơ pháp tuyến \(\overrightarrow {{n_1}} = \left( {{a_1};\,\,b{ & _1}} \right)\) và \(\overrightarrow {{n_2}} = \left( {{a_2};\,\,b{ & _2}} \right)\) tương ứng. Khi đó góc φ giữa hai đường thẳng đó được xác định bởi công thức
 Xem đáp án
Xem đáp án
Đáp án: C
Câu 29:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Khoảng cách từ điểm A(1; 1) đến d: 5x – 12y – 6 = 0 là
\(d\left( {A,\,\,d} \right) = \frac{{\left| {5 \cdot 1 - 12 \cdot 1 - 6} \right|}}{{\sqrt {{5^2} + {{\left( { - 12} \right)}^2}} }} = 1\).
Câu 30:
16/07/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Đường thẳng a có một vectơ pháp tuyến là \(\overrightarrow {{n_1}} = \left( {\sqrt 3 ;\,\, - 1} \right)\);
Đường thẳng b có một vectơ pháp tuyến là \(\overrightarrow {{n_2}} = \left( {1;\, - \sqrt 3 } \right)\).
Áp dụng công thức tính góc giữa hai đường thẳng ta có:
\(\cos \left( {a,\,\,b} \right) = \left| {\cos \left( {\overrightarrow {{n_1}} ,\,\,\overrightarrow {{n_2}} } \right)} \right| = \frac{{\left| {\overrightarrow {{n_1}} \cdot \overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right| \cdot \left| {\overrightarrow {{n_2}} } \right|}} = \frac{{\left| {\sqrt 3 \cdot 1 + \left( { - 1} \right) \cdot \left( { - \sqrt 3 } \right)} \right|}}{{\sqrt {{{\left( {\sqrt 3 } \right)}^2} + {{\left( { - 1} \right)}^2}} \cdot \sqrt {{1^2} + {{\left( { - \sqrt 3 } \right)}^2}} }} = \frac{{\sqrt 3 }}{2}\).
Suy ra góc giữa hai đường thẳng bằng 30°.
Câu 32:
17/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Câu 33:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Câu 34:
19/07/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Đường tròn có tâm I(3; 4) tiếp xúc với đường thẳng ∆: 3x + 4y – 10 = 0 nên bán kính đường tròn chính là khoảng cách từ tâm I đến đường thẳng ∆.
Ta có: R = d(I, ∆) = \(\frac{{\left| {3 \cdot 3 + 4 \cdot 4 - 10} \right|}}{{\sqrt {{3^2} + {4^2}} }} = 3\).
Vậy phương trình đường tròn cần tìm là: (x – 3)2 + (y – 4)2 = 9.
Câu 35:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Đường tròn (C) có tâm là I(2; – 2). Tiếp tuyến của (C) tại M(1; 0) có vectơ pháp tuyến \(\overrightarrow {MI} = \left( {1;\, - 2} \right)\), nên có phương trình
1(x – 1) – 2(y – 0) = 0 hay x – 2y – 1 = 0.
Câu 36:
21/07/2024Giả sử độ cao h (đơn vị: mét) của một quả bóng golf tính theo thời gian t (đơn vị: giây) trong một lần đánh của vận động viên được xác định bằng một hàm số bậc hai và giá trị tương ứng tại một số thời điểm được cho bởi bảng dưới đây:
|
Thời gian (s) |
0 |
0,5 |
1 |
2 |
3 |
|
Độ cao (m) |
0 |
28 |
48 |
64 |
48 |
a) Xác định hàm số bậc hai biểu thị độ cao h(m) của quả bóng gofl tính theo thời gian t(s).
b) Sau bao lâu kể từ khi vận động viên đánh bóng thì bóng lại chạm đất?
 Xem đáp án
Xem đáp án
Đáp án:
a) Xét hàm số bậc hai biểu thị độ cao h phụ thuộc thời gian t có dạng h(t) = at2 + bt + c, trong đó a ≠ 0. Theo đề bài:
Với t = 0, h = 0, ta có: c = 0 nên h(t) = at2 + bt. Khi đó:
+ Với t = 1, h = 48, ta có: a . 12 + b . 1 = 48 ⇔ a + b = 48.
+ Với t 2, h = 64, ta có: a . 22 + b . 2 = 64 ⇔ 4a + 2b = 64.
Giải hệ phương trình \(\left\{ \begin{array}{l}a + b = 48\\4a + 2b = 64\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 16\\b = 64\end{array} \right.\). Suy ra h(t) = – 16t2 + 64t.
Thay các giá trị tương ứng còn lại của bảng vào công thức trên, ta thấy phù hợp.
Vậy hàm số bậc hai cần tìm là h(t) = – 16t2 + 64t.
b) Bóng chạm đất khi h(t) = 0 ⇔ – 16t2 + 64t = 0.
Suy ra t = 0 hoặc t = 4.
Vậy sau 4 giây kể từ khi vận động viên đánh bóng thì bóng lại chạm đất.
Câu 37:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án:
Gọi tọa độ các điểm A, B và M là A(xA; yA); B(xB; yB) và M(xM; yM).
Vì A thuộc d1 nên 2xA – yA – 2 = 0. Suy ra yA = 2xA – 2.
Vì B thuộc d2 nên xB + yB + 3 = 0. Suy ra yB = – xB – 3.
Do M là trung điểm của đoạn AB nên
\(\left\{ \begin{array}{l}{x_A} + {x_B} = 2{x_M}\\{y_A} + {y_B} = 2{y_M}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_A} + {x_B} = 6\\\left( {2{x_A} - 2} \right) + \left( { - {x_B} - 3} \right) = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_A} = \frac{{11}}{3}\\{y_A} = \frac{{16}}{3}\end{array} \right.\).
Suy ra \(A\left( {\frac{{11}}{3};\,\,\frac{{16}}{3}} \right)\).
Đường thẳng ∆ đi qua điểm A và điểm M.
Ta có: \(\overrightarrow {AM} = \left( { - \frac{2}{3};\,\, - \frac{{16}}{3}} \right)\)\( \Rightarrow \overrightarrow {{u_{AM}}} = \left( {1;\,\,8} \right) \Rightarrow \overrightarrow {{n_{AM}}} = \left( {8;\,\, - 1} \right)\).
Đường thẳng ∆ đi qua M(3; 0) và có một vectơ pháp tuyến là \(\overrightarrow {{n_{AM}}} \) nên có phương trình là
8(x – 3) – (y – 0) = 0 hay 8x – y – 24 = 0.
Câu 38:
20/07/2024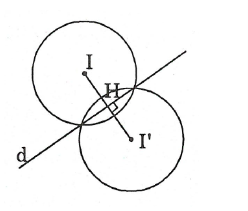
 Xem đáp án
Xem đáp án
Đáp án:
(C) có tâm I(1; 2), bán kính R = 2.
Phương trình đường thẳng ∆ đi qua I, vuông góc với d có dạng x + y + m = 0.
I (1; 2) ∈ ∆, suy ra 1 + 2 + m = 0 ⇒ m = – 3.
Do đó, phương trình đường thẳng ∆: x + y – 3 = 0.
Gọi H là giao điểm của ∆ và d. Tọa độ của H là nghiệm của hệ phương trình \[\left\{ \begin{array}{l}{\rm{x}} + {\rm{y}} - 3 = 0\\{\rm{x}} - {\rm{y}} - 1 = 0\end{array} \right.\]
Từ đó tìm được H(2; 1).
Chứng minh được H là trung điểm của II' với I' là tâm của (C'). Suy ra I'(3; 0)
Vì (C), (C') đối xứng nhau qua d nên R = R'.
Vậy phương trình (C'): (x – 3)2 + y2 = 4.
Tọa độ giao điểm của (C), (C') là nghiệm của hệ phương trình:
\[\left\{ \begin{array}{l}{\left( {{\rm{x}} - 1} \right)^2} + {\left( {{\rm{y}} - 2} \right)^2} = 4\\{\left( {{\rm{x}} - 3} \right)^2} + {y^2} = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{\left( {{\rm{x}} - 1} \right)^2} + {\left( {{\rm{y}} - 2} \right)^2} = 4\\{\rm{x}} - {\rm{y}} - 1 = 0\end{array} \right.\]
\[ \Leftrightarrow \left[ \begin{array}{l}{{\rm{x}}_{\rm{1}}} = 1 \Rightarrow {{\rm{y}}_{\rm{1}}} = 0\\{{\rm{x}}_{\rm{2}}} = 3 \Rightarrow {{\rm{y}}_2} = 2\end{array} \right. \Rightarrow {\rm{A}}\left( {1;0} \right),\,\,{\rm{B}}\left( {3;2} \right)\] là giao điểm của (C), (C').
Có thể bạn quan tâm
- Đề kiểm tra giữa học kì 2 Toán 10 Kết nối tri thức có đáp án (433 lượt thi)
Các bài thi hot trong chương
- Đề thi Học kì 1 Toán 10 - Bộ sách KNTT có đáp án (684 lượt thi)
- Đề thi Giữa kì 1 Toán 10 có đáp án (551 lượt thi)
