Bài tập Hypebol có đáp án
-
678 lượt thi
-
17 câu hỏi
-
40 phút
Danh sách câu hỏi
Câu 1:
25/06/2024Cho hypebol (H) với phương trình chính tắc và điểm M(x0; y0) nằm trên (H). Các điểm M1(–x0; y0), M2(x0; –y0), M3(–x0; –y0) có thuộc (H) không?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Nếu điểm M(x0; y0) thuộc (H) thì ta có:
Ta có: nên các điểm có toạ độ M1(–x0; y0), M2(x0; –y0), M3(–x0; –y0) cũng thuộc (H).
Câu 2:
25/06/2024Viết phương trình chính tắc của hypebol có kích thước của hình chữ nhật cơ sở là 8 và 6. Xác định đỉnh, tiêu điểm, tiêu cự, độ dài trục của hypebol này.
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Gọi phương trình chính tắc của hypebol đã cho là (a > 0, b > 0).
Hypebol kích thước của hình chữ nhật cơ sở là 8 và 6, suy ra 2a = 8, 2b = 6, suy ra a = 4 và b = 3.
Vậy phương trình chính tắc của hypebol đã cho là
Có = 42 + 32 = 25, suy ra c = 5.
Toạ độ các đỉnh của hypebol là A1(–4; 0) và A2(4; 0).
Toạ độ các tiêu điểm của hypebol là F1(–5; 0) và F2(5; 0).
Tiêu cự của hypebol là 2c = 10.
Độ dài trục thực là 2a = 8, độ dài trục ảo là 2b = 6.
Câu 3:
06/07/2024Khi bay với vận tốc siêu thanh (tốc độ chuyển động lớn hơn tốc độ âm thanh trong cùng môi trường), một máy bay tạo ra một vùng nhiễu động trên mặt đất dọc theo một nhánh của hypebol (H) (Hình 4). Phần nghe rõ nhất tiếng ồn của vùng nói trên được gọi là thảm nhiễu động. Bề rộng của thảm này gấp khoảng 5 lần cao độ của máy bay. Tính cao độ của máy bay, biết bề rộng của thảm nhiễu động được đo cách phía sau máy bay một khoảng là 40 mile (mile (dặm) là đơn vị đo khoảng cách, 1 mile ≈ 1,6 km ) và (H) có phương trình:
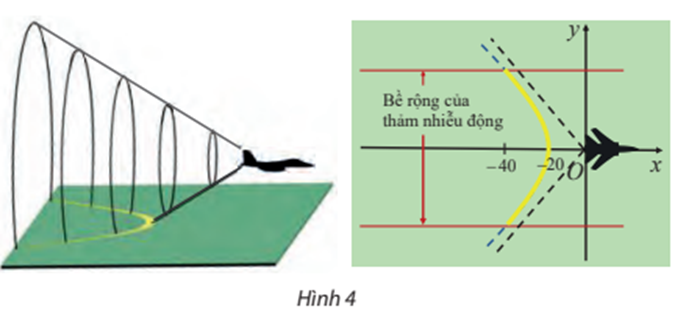
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Khi x = 40 thì
=> Bề rộng của thảm nhiễu là (mile)
=> Cao độ của máy bay là ≈ 6,93 (mlie)
Vậy cao độ của máy bay là khoảng 6,93 dặm.
Câu 4:
21/07/2024Cho điểm M(x; y) nằm trên hypebol .
a) Chứng minh rằng F1M2 – F2M2 = 4cx.
b) Giả sử điểm M(x; y) thuộc nhánh đi qua A1(–a; 0) (Hình 5a). Sử dụng kết quả đã chứng minh được ở câu a) kết hợp với tính chất MF2 – MF1 = 2a đã biết để chứng minh . Từ đó, chứng minh các công thức: ;
b) Giả sử điểm M(x; y) thuộc nhánh đi qua A2(a; 0) (Hình 5 b). Sử dụng kết quả đã chứng minh được ở câu a) kết hợp với tính chất MF1 – MF2 = 2a đã biết để chứng minh . Từ đó, chứng minh các công thức: ;
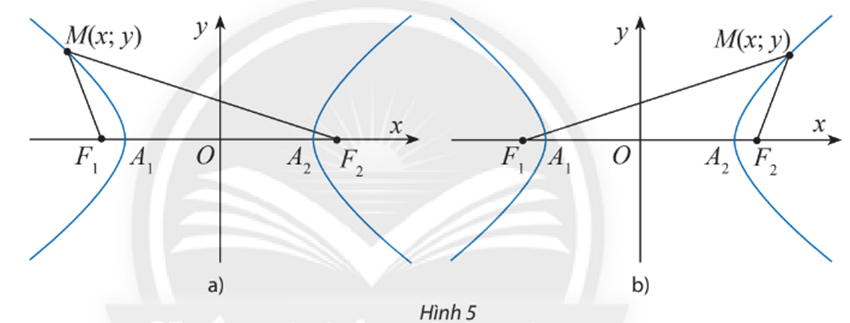
 Xem đáp án
Xem đáp án
Hướng dẫn giải
a) F1M2 = + = + = ;
F2M2 = +=
F1M2 – F2M2 = () – () = 4cx.
b) Ta có: MF12 – MF22 = 4cx => (MF1 + MF2)(MF1 – MF2) = 4cx => (MF1 + MF2)(–2a) = 4cx
=> MF1 + MF2 = = –x. Khi đó:
(MF1 + MF2) + (MF1 – MF2) = – + (–2a) => 2MF1 = –
=> MF1 =
(MF1 + MF2) – (MF1 – MF2) = – – (–2a) => 2MF2 = - + 2a
=> MF2 = a –c/a x.
c) Ta có: MF12 – MF22 = 4cx => (MF1 + MF2)(MF1 – MF2) = 4cx => (MF1 + MF2)2a = 4cx
=> MF1 + MF2 = = x. Khi đó:
(MF1 + MF2) + (MF1 – MF2) = + 2a => 2MF1 = + 2a
=> MF1 = a + x.
(MF1 + MF2) – (MF1 – MF2) = – 2a => 2MF2 = – 2a
=> MF2 = – a +x.
Câu 5:
25/06/2024Tính độ dài hai bán kính qua tiêu của điểm M(x; y) trên hypebol .
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Có = 36, suy ra a = 8, b = 6, c =
Độ dài hai bán kính qua tiêu của điểm M(x; y) là:
MF1 = MF2 =
Câu 6:
25/06/2024Tính độ dài hai bán kính qua tiêu của đỉnh A2(a; 0) trên hypebol (H): .
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Độ dài hai bán kính qua tiêu của đỉnh A2(a; 0) là:
A2F1 = (vì a + c > 0 );
A2F2 = (vì a – c < 0).
Câu 8:
25/06/2024Tìm tâm sai của các hypebol sau:
a) ;
b) ;
c) .
 Xem đáp án
Xem đáp án
Hướng dẫn giải
a) Có , suy ra a = 2, b = 1, c =
=> tâm sai của hypebol là e =
b) Có , suy ra a = 3, b = 5, c =
=> tâm sai của hypebol là e =
c) Có , suy ra a = b = c =
=> tâm sai của hypebol là e =
Câu 9:
16/07/2024Cho hypebol (H) có tâm sai bằng . Chứng minh trục thực và trục ảo của (H) có độ dài bằng nhau.
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Giả sử hypebol (H) có phương trình chính tắc là (a > 0, b > 0).
Hypebol (H) có tâm sai bằng
Vậy trục thực và trục ảo của (H) có độ dài bằng nhau.
Câu 10:
14/07/2024Một vật thể có quỹ đạo là một nhánh của hypebol (H), nhận tâm Mặt Trời làm tiêu điểm (Hình 6). Cho biết tâm sai của (H) bằng 1,2 và khoảng cách gần nhất giữa vật thể và tâm Mặt Trời là 2 . 108 km.
a) Lập phương trình chính tắc của (H).
b) Lập công thức tính bán kính qua tiêu của vị trí M(x; y) của vật thể trong mặt phẳng toạ độ.
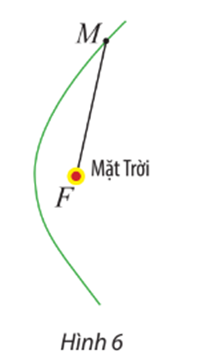
 Xem đáp án
Xem đáp án
Hướng dẫn giải
a) Chọn hệ trục toạ độ sao cho tiêu điểm F2 của (H) trùng với tâm Mặt Trời, trục Ox đi qua đỉnh và tiêu điểm này của (H), đơn vị trên các trục là km.
Gọi phương trình chính tắc của (H) là (a > 0, b > 0).
Gọi toạ độ của vật thể là M(x; y).
Áp dụng công thức bán kính qua tiêu, ta có: khoảng cách giữa vật thể và tâm Mặt Trời là MF2 = = ex – a ≥ ea – a (vì vật thể nằm ở nhánh bên phải trục Ox nên x ≥ a).
Như vậy khoảng cách gần nhất giữa vật thể và tâm Mặt Trời là ea – a
=> ea – a = 2 . 108 => 1,2a – a = 2 . 108 => a = 109 =>c = ea = 1,2 . 109
Vậy phương trình chính tắc của (H) là
b) Bán kính qua tiêu của vị trí M(x; y) của vật thể trong mặt phẳng toạ độ là:
MF2 = = |109 – 1,2x| (km).
Câu 11:
23/07/2024Cho điểm M(x; y) trên hypebol và hai đường thẳng ; (Hình 7).
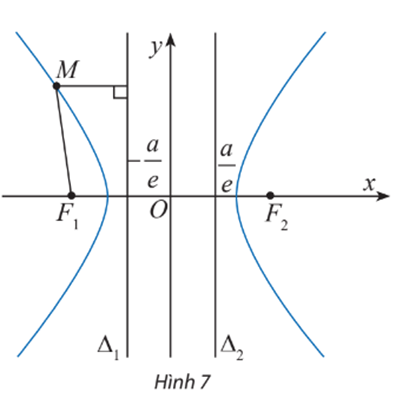
Gọi d(M; Δ1), d(M; Δ2) lần lượt là khoảng cách từ M đến các đường thẳng Δ1, Δ2.
Ta có: .
Dựa theo cách tính trên, tính .
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Ta viết lại phương trình đường thẳng Δ2 ở dạng: Với mỗi điểm M(x; y) thuộc hypebol, ta có:
suy ra
Câu 12:
05/07/2024Tìm toạ độ hai tiêu điểm và viết phương trình hai đường chuẩn tương ứng của các hypebol sau:
a)
b)
c) .
 Xem đáp án
Xem đáp án
Hướng dẫn giải
a) Có , suy ra c =
=> Hai tiêu điểm của hypebol là và
Phương trình đường chuẩn ứng với tiêu điểm F1 là
Phương trình đường chuẩn ứng với tiêu điểm F2 là
b) Có , suy ra c =
=> Hai tiêu điểm của hypebol là và
Phương trình đường chuẩn ứng với tiêu điểm F1 là
Phương trình đường chuẩn ứng với tiêu điểm F2 là
c) Có , suy ra c =
=> Hai tiêu điểm của hypebol là và
Phương trình đường chuẩn ứng với tiêu điểm F1 là
Phương trình đường chuẩn ứng với tiêu điểm F2 là
Câu 13:
27/06/2024Lập phương trình chính tắc của hypebol có tiêu cự bằng 26 và khoảng cách giữa hai đường chuẩn bằng 288/13.
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Gọi phương trình chính tắc của hypebol đã cho là (a > 0, b > 0).
+) Hypebol có tiêu cự bằng 26, suy ra 2c = 26, suy ra c = 13.
+) Khoảng cách giữa hai đường chuẩn bằng 288/13, suy ra
Vậy phương trình chính tắc của hypebol đã cho là
Câu 14:
13/07/2024Cho hypebol .
a) Tìm tâm sai và độ dài hai bán kính qua tiêu của điểm trên (H).
b) Tìm tọa độ hai tiêu điểm và viết phương trình hai đường chuẩn tương ứng.
c) Tìm điểm N(x; y) (H) sao cho NF1 = 2NF2 với F1, F2 là hai tiêu điểm của (H).
 Xem đáp án
Xem đáp án
Hướng dẫn giải
a) Có => a = 12, b = 5,
Tâm sau của (H) là e =
Độ dài hai bán kính qua tiêu của điểm là:
MF1 =
MF2 =
b) Hai tiêu điểm của hypebol là F1(–13; 0) và F2(13; 0).
Phương trình đường chuẩn ứng với tiêu điểm F1 là
Phương trình đường chuẩn ứng với tiêu điểm F2 là
c) NF1 = NF2 =
NF1 = 2NF2
+) x = 48/13 loại vì 0 < x < a.
+) x = 432/13 thì
Vậy có hai điểm N thoả mãn đề bài là N1 và N2
Câu 15:
22/07/2024Lập phương trình chính tắc của hypebol có tiêu cự bằng 20 và khoảng cách giữa hai đường chuẩn bằng 36/5.
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Gọi phương trình chính tắc của hypebol đã cho là (a > 0, b > 0).
+) Hypebol có tiêu cự bằng 26, suy ra 2c = 20, suy ra c = 10.
+) Khoảng cách giữa hai đường chuẩn bằng 36/5, suy ra
Vậy phương trình chính tắc của hypebol đã cho là
Câu 16:
22/07/2024Cho đường tròn (C) tâm F1, bán kính r và một điểm F2 thoả mãn F1F2 = 4r.
a) Chứng tỏ rằng tâm của các đường tròn đi qua F2 và tiếp xúc với (C) nằm trên một đường hypebol (H).
b) Viết phương trình chính tắc và tìm tâm sai của (H).
 Xem đáp án
Xem đáp án
Hướng dẫn giải
a) Gọi (C'; r') là đường tròn đi qua F2 và tiếp xúc với (C);
I(x; y) là tâm của đường tròn đi qua F2 và tiếp xúc với (C).
Vì F2 nằm ngoài (C) nên (C') tiếp xúc ngoài với (C) hoặc (C') tiếp xúc trong với (C) và (C) nằm trong (C').
+) Nếu (C') tiếp xúc ngoài với (C) thì r' + r = IF1 => IF2 + r = IF1 => IF1 – IF2 = r
+) Nếu (C') tiếp xúc trong với (C) và (C) nằm trong (C') thì r' – r = IF1 => IF2 – r = IF1
=> IF2 – IF1 = r.
Vậy ta luôn có |IF2 – IF1| = r trong cả hai trường hợp
=> I nằm trên hypebol có hai tiêu điểm là F1, F2 và độ dài trục thực là r.
b) Chọn hệ trục toạ độ sao cho gốc toạ độ trùng với trung điểm của F1F2 và F1, F2 đều nằm trên trục Ox.
Giả sử phương trình chính tắc của hypebol này là (a > 0, b > 0).
Khi đó ta có 2a = r, suy ra a = r/2
F1F2 = 4r, suy ra c = 2r, suy ra
Vậy phương trình chính tắc của hypebol này là
Câu 17:
20/07/2024Trong hoạt động mở đầu bài học, cho biết khoảng cách giữa hai trạm vô tuyến là 600 km, vận tốc sóng vô tuyến là 300000 km/s và thời gian con tàu nhận được tín hiệu từ hai trạm trên bờ biển luôn cách nhau 0,0012 s (hai trạm vô tuyến phát các tín hiệu cùng một thời điểm). Viết phương trình chính tắc của quỹ đạo hypebol (H) của con tàu.
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Chọn hệ trục toạ độ sao cho gốc toạ độ O trùng với tiêu điểm của F1F2, đơn vị trên các trục là km.
Giả sử phương trình chính tắc của (H) là (a > 0, b > 0).
Gọi t1 là thời gian con tàu nhận được tín hiệu từ trạm F1; t2 là thời gian con tàu nhận được tín hiệu từ trạm F2, v là vận tốc sóng vô tuyến.
Theo đề bài ta có: |t1 – t2| = 0,0012
=>|vt1 – vt2| = 0,0012v = 0,0012 . 300000 = 360 (km)
=>|MF1 – MF2| = 360 với mọi vị trí của M
=> 2a = 360 => a = 180.
Có khoảng cách giữa hai trạm vô tuyến là 600 km => 2c = 600 => c = 300
Vậy phương trình chính tắc của (H) là
