Giáo án Phương trình quy về phương trình bậc nhất một ẩn (Cánh diều) Toán 9

Chỉ từ 500k mua trọn bộ Giáo án Toán 9 Cánh diều bản word (cả năm) trình bày đẹp:

B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận giáo án.

Xem thử tài liệu tại đây: Link tài liệu

Giáo án Toán 9 Bài 1 (Cánh diều): Phương trình quy về phương trình bậc nhất một ẩn

I. MỤC TIÊU

1. Kiến thức: Học xong bài này, HS đạt các yêu cầu sau:

– Nhận biết được dạng tổng quát của phương trình tích và cách giải phương trình tích.

– Nhận biết được phương trình chứa ẩn ở mẫu và cách giải phương trình chứa ẩn ở mẫu.

– Giải được phương trình tích và phương trình chứa ẩn ở mẫu cơ bản.

– Vận dụng dạng phương trình quy về phương trình bậc nhất một ẩn để giải các bài toán thực tế.

2. Năng lực

* Năng lực chung:

– Năng lực tự chủ và tự học trong tìm tòi khám phá.

– Năng lực giao tiếp và hợp tác trong trình bày, thảo luận và làm việc nhóm.

– Năng lực giải quyết vấn đề và sáng tạo trong thực hành, vận dụng.

* Năng lực riêng:

– Năng lực tư duy và lập luận toán học: Được hình thành thông qua các thao tác như phân tích dữ liệu, lập luận để tìm được cách giải phương trình tích và phương trình chứa ẩn ở mẫu.

– Năng lực giao tiếp toán học: Được hình thành qua việc HS sử dụng được các thuật ngữ toán học xuất hiện ở bài học trong trình bày, diễn đạt giải toán như phương trình tích, phương trình chứa ẩn ở mẫu, điều kiện xác định của phương trình.

– Năng lực mô hình hóa toán học: Được hình thành thông qua thao tác HS viết được phương trình quy về phương trình bậc nhất một ẩn để mô tả tình huống xuất hiện trong một số bài toán thực tế đơn giản.

– Năng lực giải quyết vấn đề toán học: Được hình thành qua việc HS phát hiện được vấn đề cần giải quyết và sử dụng được kiến thức, kĩ năng toán học trong bài học để giải quyết vấn đề.

3. Phẩm chất

– Có ý thức học tập, ý thức tìm tòi, khám phá và sáng tạo, có ý thức làm việc nhóm.

– Chăm chỉ tích cực xây dựng bài, có trách nhiệm, chủ động chiếm lĩnh kiến thức theo sự hướng dẫn của GV.

– Hình thành tư duy logic, lập luận chặt chẽ, và linh hoạt trong quá trình suy nghĩ.

II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU

1. Đối với GV: SGK, Tài liệu giảng dạy, giáo án powerpoint, đồ dùng dạy học, thước thẳng có chia khoảng.

2. Đối với HS: SGK, SBT, vở ghi, giấy nháp, đồ dùng học tập (bút, thước...), bảng nhóm, bút viết bảng nhóm.

III. TIẾN TRÌNH DẠY HỌC

A. HOẠT ĐỘNG KHỞI ĐỘNG (MỞ ĐẦU)

a) Mục tiêu:

‒ Gợi mở động cơ dẫn đến nhu cầu giải bài toán bằng cách lập phương trình quy về phương trình bậc nhất một ẩn.

‒ Tình huống mở đầu thực tế, gần gũi làm gợi tâm thế, tạo hứng thú học tập.

b) Nội dung: HS đọc bài toán mở đầu và thực hiện bài toán dưới sự dẫn dắt của GV (HS chưa cần giải bài toán ngay).

c) Sản phẩm: HS nắm được các thông tin trong bài toán và dự đoán câu trả lời cho câu hỏi mở đầu theo ý kiến cá nhân.

d) Tổ chức thực hiện:

Bước 1: Chuyển giao nhiệm vụ:

- GV chiếu Slide dẫn dắt, đặt vấn đề qua bài toán mở đầu và yêu cầu HS thảo luận và nêu dự đoán (chưa cần HS giải):

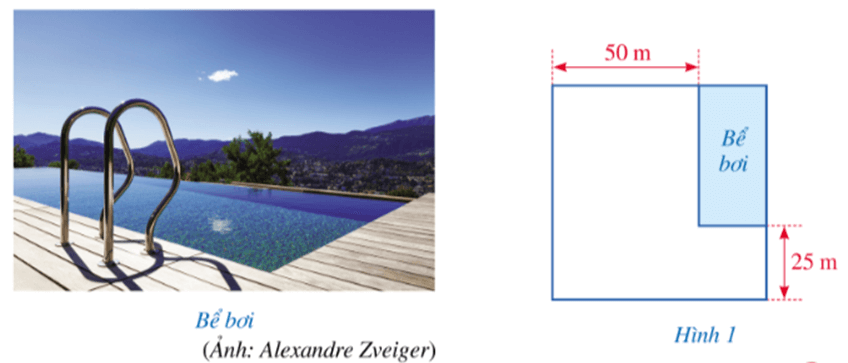
“Trên một khu đất có dạng hình vuông, người ta dành một mảnh đất có dạng hình chữ nhật ở góc của khu đất để làm bể bơi (Hình 1). Biết diện tích của bể bơi bằng $1250m^2$

Câu hỏi: Độ dài cạnh của khu đất bằng bao nhiêu mét?”

Bước 2: Thực hiện nhiệm vụ: HS quan sát và chú ý lắng nghe, thảo luận nhóm và thực hiện yêu cầu theo dẫn dắt của GV.

Bước 3: Báo cáo, thảo luận: GV gọi đại diện một số thành viên nhóm HS trả lời, HS khác nhận xét, bổ sung.

Bước 4: Kết luận, nhận định: GV ghi nhận câu trả lời của HS, trên cơ sở đó dẫn dắt HS vào tìm hiểu bài học mới: “Bài 1. Phương trình quy về phương trình bậc nhất một ẩn”.

B. HÌNH THÀNH KIẾN THỨC MỚI

Hoạt động 1: Phương trình tích có dạng $\left(ax+b\right)\left(cx+d\right)=0$$\left(a\ne 0,c\ne 0\right)$

a) Mục tiêu:

‒ HS nhận biết được dạng tổng quát của phương trình tích và cách giải của phương trình tích;

‒ HS giải được phương trình tích cơ bản;

‒ HS vận dụng được cách giải phương trình tích để giải các bài toán thực tế.

b) Nội dung:

– HS tìm hiểu nội dung kiến thức về dạng tổng quát của phương trình tích và cách giải phương trình tích theo yêu cầu, dẫn dắt của GV và thực hiện HĐ1, đọc và thảo luận Ví dụ 1, Ví dụ 2, Ví dụ 3, thực hành làm Luyện tập 1, Luyện tập 2.

c) Sản phẩm: HS hình thành được kiến thức, nắm được dạng tổng quát của phương trình tích và cách giải phương trình tích.

d) Tổ chức thực hiện:

HOẠT ĐỘNG CỦA GV VÀ HS

SẢN PHẨM DỰ KIẾN

Bước 1. Chuyển giao nhiệm vụ: Tìm hiểu dạng tổng quát của phương trình tích và cách giải phương trình tích – GV yêu cầu HS thực hiện HĐ1: + GV mời một số HS trả lời câu a). + GV mời 2 HS trình bày bảng ý 1 câu b). + GV có thể yêu cầu HS nhắc lại điều kiện để một số là nghiệm của phương trình bậc nhất một ẩn. + GV mời một số HS trình bày ý 2 và ý 3 câu b). + Các bạn HS còn lại trình bày vào vở và nhận xét bài của bạn. + GV đánh giá và chốt đáp án.

I. Phương trình tích có dạng $\left(ax+b\right)\left(cx+d\right)=0$ $\left(a\ne 0,c\ne 0\right)$ HĐ1: a) Ta thấy, $uv=0$ khi $u=0$ hoặc $v=0.$ b) ⦁ Giải phương trình: ⦁ Thay $x=3$ vào vế trái phương trình $\left(x–3\right)\left(2x+1\right)=0,$ ta được: $VT=\left(3–3\right)\left(2\cdot 3+1\right)$$=0\cdot 7=0=VP$ Thay $x=-\frac{1}{2}$ vào vế trái phương trình $\left(x–3\right)\left(2x+1\right)=0,$ ta được: Do đó nghiệm của phương trình $x–3=0$ và $2x+1=0$ là nghiệm của phương trình $\left(x–3\right)\left(2x+1\right)=0.$ ⦁ Vì $x=x_0$ là nghiệm của phương trình $\left(x–3\right)\left(2x+1\right)=0$ nên ta có: $\left(x_0–3\right)\left(2x_0+1\right)=0$ $x_0–3=0$ hoặc $2x_0+1=0$ Vậy $x_0$ là nghiệm của phương trình $x–3=0$ hoặc phương trình $2x+1=0.$

................................

................................

................................