Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
• Hình 10a):
Tứ giác MNPQ có hai đường chéo cắt nhau MP và NQ tại trung điểm O của mỗi đường nên là hình bình hành.
Lại có hai đường chéo MP và NQ vuông góc với nhau tại O nên hình bình hành MNPQ là hình thoi (1)
Mặt khác: MP = OM + OP = 2OM
NQ = ON + OQ = 2ON
Mà OM = ON nên MP = NQ.
Ta có MNPQ là hình thoi nên cũng là hình bình hành.
Mà hai đường chéo MP và NQ bằng nhau nên hình bình hành MNPQ là hình chữ nhật (2)
Từ (1) và (2) suy ra MNPQ là hình vuông.
• Hình 10b):
Tứ giác RSTU có RS = ST = TU = UR nên là hình thoi (1)
Do đó RSTU cũng là hình bình hành.
Lại có nên hình bình hành RSTU là hình chữ nhật (2)
Từ (1) và (2) suy ra RSTU là hình vuông.
• Hình 10a):
Tứ giác MNPQ có hai đường chéo cắt nhau MP và NQ tại trung điểm O của mỗi đường nên là hình bình hành.
Lại có hai đường chéo MP và NQ vuông góc với nhau tại O nên hình bình hành MNPQ là hình thoi (1)
Mặt khác: MP = OM + OP = 2OM
NQ = ON + OQ = 2ON
Mà OM = ON nên MP = NQ.
Ta có MNPQ là hình thoi nên cũng là hình bình hành.
Mà hai đường chéo MP và NQ bằng nhau nên hình bình hành MNPQ là hình chữ nhật (2)
Từ (1) và (2) suy ra MNPQ là hình vuông.
• Hình 10b):
Tứ giác RSTU có RS = ST = TU = UR nên là hình thoi (1)
Do đó RSTU cũng là hình bình hành.
Lại có nên hình bình hành RSTU là hình chữ nhật (2)
Từ (1) và (2) suy ra RSTU là hình vuông.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 5:
Cho tứ giác ABCD có bốn góc bằng nhau và có bốn cạnh bằng nhau. Hãy chứng tỏ ABCD vừa là hình thoi vừa là hình chữ nhật.
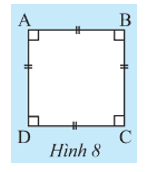
Cho tứ giác ABCD có bốn góc bằng nhau và có bốn cạnh bằng nhau. Hãy chứng tỏ ABCD vừa là hình thoi vừa là hình chữ nhật.

Câu 6:
Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Giải thích các khẳng định sau:
a) Nếu là góc vuông thì và cũng là góc vuông.
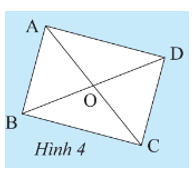
Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Giải thích các khẳng định sau:
a) Nếu là góc vuông thì và cũng là góc vuông.

Câu 7:
Dùng thước đo góc để đo số đo các góc ở Hình 1 và rút ra nhận xét về số đo của chúng.
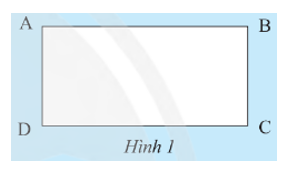
Dùng thước đo góc để đo số đo các góc ở Hình 1 và rút ra nhận xét về số đo của chúng.

Câu 8:
Lấy một tờ giấy, gấp làm tư để có một góc vuông như trong Hình 16, dùng kéo cắt theo đường MN sao cho OM = ON. Mở phần giấy cắt được ra ta được một tứ giác.
Tứ giác đó là hình gì? Giải thích kết luận của em.
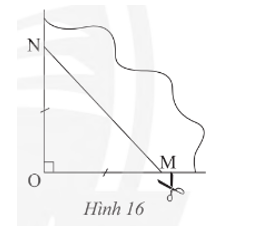
Lấy một tờ giấy, gấp làm tư để có một góc vuông như trong Hình 16, dùng kéo cắt theo đường MN sao cho OM = ON. Mở phần giấy cắt được ra ta được một tứ giác.
Tứ giác đó là hình gì? Giải thích kết luận của em.

Câu 9:
Cho hình vuông MNPQ. Chứng minh MNPQ vừa là hình chữ nhật vừa là hình thoi.
Cho hình vuông MNPQ. Chứng minh MNPQ vừa là hình chữ nhật vừa là hình thoi.
Câu 10:
Trong Hình 12, cho biết ABCD là một hình vuông. Chứng minh rằng:
a) Tứ giác EFGH có ba góc vuông;
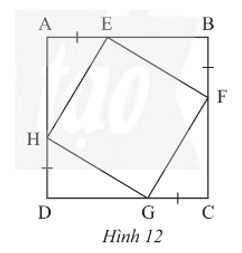
Trong Hình 12, cho biết ABCD là một hình vuông. Chứng minh rằng:
a) Tứ giác EFGH có ba góc vuông;

Câu 11:
Cho tam giác ABC có đường cao AH. Gọi I là trung điểm của AC, E là điểm đối xứng với H qua I. Gọi M, N lần lượt là trung điểm của HC, CE. Các đường thẳng AM, AN cắt HE tại G và K.
a) Chứng minh tứ giác AHCE là hình chữ nhật.
Cho tam giác ABC có đường cao AH. Gọi I là trung điểm của AC, E là điểm đối xứng với H qua I. Gọi M, N lần lượt là trung điểm của HC, CE. Các đường thẳng AM, AN cắt HE tại G và K.
a) Chứng minh tứ giác AHCE là hình chữ nhật.
Câu 14:
Chỉ được sử dụng compa, hãy kiểm tra tứ giác ở Hình 6 có phải là hình chữ nhật hay không.
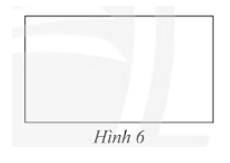
Chỉ được sử dụng compa, hãy kiểm tra tứ giác ở Hình 6 có phải là hình chữ nhật hay không.

Câu 15:
Cho hình thoi ABCD. Hãy chứng tỏ:
a) Nếu là góc vuông thì ba góc còn lại của hình thoi cũng là góc vuông.
b) Nếu AC = BD thì là góc vuông.
Cho hình thoi ABCD. Hãy chứng tỏ:
a) Nếu là góc vuông thì ba góc còn lại của hình thoi cũng là góc vuông.
b) Nếu AC = BD thì là góc vuông.