Thể tích V của khối lăng trụ tam giác đều có tất cả các cạnh bằng a là

Đáp án đúng: D

*Lời giải:

*Phương pháp giải:

áp dụng công thức tính thể tích khối lăng trụ tam giác đều: V =B.h

*Lý thuyết nắm thêm về khối trụ, khối nón, mặt cầu:

1_MẶT NÓN:

Hình nón tròn xoay và khối nón tròn xoay.

a) Cho tam giác OIM vuông tại I. Khi quay tam giác đó xung quanh cạnh góc vuông OI thì đường gấp khúc OMI tạo thành một hình được gọi là hình nón tròn xoay, gọi tắt là hình nón.

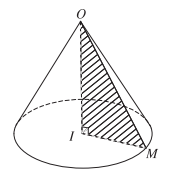
Hình tròn tâm I sinh bởi các điểm thuộc cạnh IM khi quay quanh trục OI được gọi là mặt đáy của hình nón, điểm O được gọi là đỉnh của hình nón.

Độ dài đoạn OI gọi là chiều cao của hình nón, đó cũng chính là khoảng cách từ O đến mặt phẳng đáy. Độ dài đoạn OM gọi là độ dài đường sinh của hình nón.

Phần mặt tròn xoay được sinh ra bởi các điểm trên cạnh OM khi quay quanh OI được gọi là mặt xung quanh của hình nón đó.

Diện tích xung quanh của hình nón tròn xoay.

a) Một hình chóp được gọi là nội tiếp một hình nón nếu đáy của hình chóp là đa giác nội tiếp đường tròn đáy của hình nón và đỉnh của hình chóp là đỉnh của hình nón. Khi đó, ta còn nói hình nón ngoại tiếp hình chóp.

a_Định nghĩa: Diện tích xung quanh của hình nón tròn xoay là giới hạn của diện tích xung quanh của hình chóp đều nội tiếp hình nón đó khi số cạnh đáy tăng lên vô hạn.

Công thức tính diện tích xung quanh của hình nón.

- Diện tích xung quanh của hình nón tròn xoay bằng một nửa tích của độ dài đường tròn đáy và độ dài đường sinh.

$S_{xq}=\pi rl$ (r là bán kính đường tròn đáy, l là độ dài đường sinh).

- Người ta gọi tổng của diện tích xung quanh và diện tích đáy là diện tích toàn phần của hình nón.

- Chú ý: Diện tích xung quanh, diện tích toàn phần của hình nón tròn xoay cũng là diện tích xung quanh , diện tích toàn phần của khối nón được giới hạn bởi hình nón đó.

Thể tích khối nón tròn xoay.

a) Định nghĩa.

Thể tích của khối nón tròn xoay là giới hạn của thể tích khối chóp đều nội tiếp khối nón đó khi số cạnh đáy tăng lên vô hạn.

b) Công thức tính thể tích khối nón tròn xoay.

Gọi V là thể tích của khối nón tròn xoay có diện tích đáy B và chiều cao h, ta có công thức: $\text{}V=\frac{1}{3}B.h$

Như vậy, nếu bán kính đáy bằng r thì $B=\pi r^2$, khi đó: $\text{}V=\frac{1}{3}\pi r^2.h$.

2_MẶT TRỤ

a) Định nghĩa

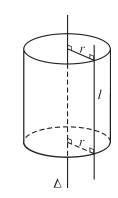
Trong mặt phẳng (P) cho hai đường thẳng ∆ và l song song với nhau, cách nhau một khoảng bằng r. Khi quay mặt phẳng (P) xung quanh ∆ thì đường thẳng l sinh ra một mặt tròn xoay được gọi là mặt trụ tròn xoay.

Người ta thường gọi tắt mặt trụ tròn xoay này là mặt trụ. Đường thẳng ∆ gọi là trục, đường thẳng l là đường sinh và r là bán kính của mặt trụ đó.

Diện tích xung quanh của hình trụ tròn xoay.

a) Một hình lăng trụ gọi là nội tiếp một hình trụ nếu hai đáy của hình lăng trụ nội tiếp hai đường tròn đáy của hình trụ. Khi đó, ta còn nói hình trụ ngoại tiếp hình lăng trụ.

- Định nghĩa: Diện tích xung quanh của hình trụ tròn xoay là giới hạn của diện tích xung quanh của hình lăng trụ đều nội tiếp hình trụ đó khi số cạnh đáy tăng lên vô hạn.

b) Công thức tính diện tích xung quanh của hình trụ.

- Diện tích xung quanh của hình trụ tròn xoay bằng tích của độ dài đường tròn đáy và độ dài đường sinh:

$S_{xq}=2\pi rl$ (r là bán kính của hình trụ, l là độ dài đường sinh của hình trụ).

- Chú ý: Diện tích xung quanh, diện tích toàn phần của hình trụ tròn xoay cũng là diện tích xung quanh, diện tích toàn phần của khối trụ được giới hạn bởi hình trụ đó.

Thể tích khối trụ tròn xoay.

a) Định nghĩa: Thể tích của khối trụ tròn xoay là giới hạn của thể tích khối lăng trụ đều nội tiếp khối trụ đó khi số cạnh đáy tăng lên vô hạn.

b) Công thức tính thể tích khối trụ tròn xoay.

Gọi V là thể tích của khối trụ tròn xoay có diện tích đáy B và chiều cao h, ta có công thức: V = B.h.

Như vậy, nếu bán kính đáy bằng r thì $B=\pi r^2$, khi đó: $V=\pi r^{2}h$

 3_MẶT CẦU

- Tập hợp những điểm M trong không gian cách điểm O cố định một khoảng không đổi bằng r (r > 0) được gọi là mặt cầu tâm O, bán kính r.

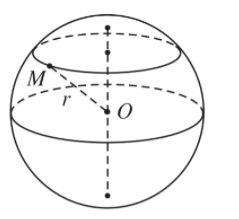
Ta kí hiệu mặt cầu tâm O, bán kính r là S(O; r) hay viết tắt là (S). Như vậy ta có mặt cầu S(O; r) = {M| OM = r}.

- Nếu hai điểm C; D nằm trên mặt cầu S(O; r) thì đoạn thẳng CD được gọi là dây cung của mặt cầu đó.

- Dây cung AB đi qua tâm O được gọi là một đường kính của mặt cầu. Khi đó, độ dài đường kính bằng 2r.

Điểm nằm trong và nằm ngoài mặt cầu. Khối cầu.

Cho mặt cầu tâm O bán kính r và A là một điểm bất kì trong không gian.

- Nếu OA = r thì ta nói điểm A nằm trên mặt cầu S(O; r).

- Nếu OA < r thì ta nói điểm A nằm trong mặt cầu S(O; r).

- Nếu OA > r thì ta nói điểm A nằm ngoài mặt cầu S(O; r).

Tập hợp các điểm thuộc mặt cầu S(O; r) cùng với các điểm nằm trong mặt cầu đó được gọi là khối cầu hoặc hình cầu tâm O, bán kính r.

Công thức tính diện tích mặt cầu và thể tích khối cầu.

- Mặt cầu bán kính r có diện tích là: $S=4\pi r^2$.

- Khối cầu bán kính r có thể tích là: $V=\frac{4}{3}\pi r^3$.

- Chú ý:

a) Diện tích S của mặt cầu bán kính r bằng bốn lần diện tích hình tròn lớn của mặt cầu đó.

b) Thể tích V của khối cầu bán kính r bằng thể tích khối chóp có diện tích đáy bằng diện tích mặt cầu và có chiều cao bằng bán kính của khối cầu đó.

Xem thêm các bài viết liên quan hay, chi tiết:

Lý thuyết Ôn tập chương 2: Mặt trụ, mặt nón, mặt cầu (mới 2024 + Bài Tập) – Toán 12 

Các dạng bài tập Mặt nón, Mặt trụ, Mặt cầu