Câu hỏi:
17/06/2026 361
Nguồn sóng có phương trình \({u_0} = 5\cos \left( {2\pi t + \frac{\pi }{6}} \right)(cm)\). Biết sóng lan truyền với bước sóng \(40\;cm\). Coi biên độ sóng không đổi. Phương trình dao động của sóng tại điểm \(M\) cách \(O\) một đoạn \(10\;cm\) nằm trên phương truyền sóng là:
Nguồn sóng có phương trình \({u_0} = 5\cos \left( {2\pi t + \frac{\pi }{6}} \right)(cm)\). Biết sóng lan truyền với bước sóng \(40\;cm\). Coi biên độ sóng không đổi. Phương trình dao động của sóng tại điểm \(M\) cách \(O\) một đoạn \(10\;cm\) nằm trên phương truyền sóng là:
A. \({u_M} = 5\cos \left( {2\pi t + \frac{\pi }{6}} \right)(cm)\).
B. \({u_M} = 5\cos \left( {2\pi t + \frac{\pi }{3}} \right)(cm)\).
B. \({u_M} = 5\cos \left( {2\pi t + \frac{\pi }{3}} \right)(cm)\).
C. \({u_M} = 5\cos \left( {2\pi t - \frac{\pi }{3}} \right)(cm)\).
D. \({u_M} = 5\cos \left( {2\pi t - \frac{\pi }{6}} \right)(cm)\)
D. \({u_M} = 5\cos \left( {2\pi t - \frac{\pi }{6}} \right)(cm)\)
Trả lời:
Giải bởi Vietjack
Ta có: \(\begin{array}{l}{u_M} = 5.\cos (2\pi .t + \frac{\pi }{6} - \frac{{2\pi .x}}{\lambda })\\\,\,\,\,\,\,\, = 5.\cos (2\pi .t + \frac{\pi }{6} - \frac{{2\pi .10\,cm}}{{40\,cm}}) = 5.\cos (2\pi .t - \frac{\pi }{3})\end{array}\)
Chọn đáp án C
Ta có: \(\begin{array}{l}{u_M} = 5.\cos (2\pi .t + \frac{\pi }{6} - \frac{{2\pi .x}}{\lambda })\\\,\,\,\,\,\,\, = 5.\cos (2\pi .t + \frac{\pi }{6} - \frac{{2\pi .10\,cm}}{{40\,cm}}) = 5.\cos (2\pi .t - \frac{\pi }{3})\end{array}\)
Chọn đáp án C
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Hai vật A và B dao động điều hòa cùng tần số. Hình bên là đồ thị biểu diễn sự phụ thuộc của li độ x1 của A và li độ x2 của B theo thời gian t. Hai dao động của A và B lệch pha nhau:
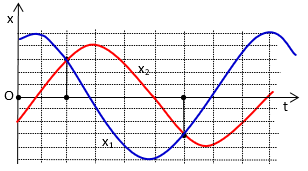
Hai vật A và B dao động điều hòa cùng tần số. Hình bên là đồ thị biểu diễn sự phụ thuộc của li độ x1 của A và li độ x2 của B theo thời gian t. Hai dao động của A và B lệch pha nhau:
Câu 2:
Con lắc đơn có chiều dài \(l\), đặt ở nơi có \(g = {\pi ^2}\;m/{s^2}\). Con lắc này dao động dưới tác dụng của ngoại lực \(F = 40\cos (\pi t)N\) thì con lắc dao động có biên độ cực đại. Tính chiều dài con lắc
Con lắc đơn có chiều dài \(l\), đặt ở nơi có \(g = {\pi ^2}\;m/{s^2}\). Con lắc này dao động dưới tác dụng của ngoại lực \(F = 40\cos (\pi t)N\) thì con lắc dao động có biên độ cực đại. Tính chiều dài con lắc
Câu 3:
Một vật dao động điều hoà có phương trình dao động \(x = 2\sin (5\pi t + \pi /3)cm\). Vận tốc của vật ở thời điểm \(t = 2(\;s)\) là
Một vật dao động điều hoà có phương trình dao động \(x = 2\sin (5\pi t + \pi /3)cm\). Vận tốc của vật ở thời điểm \(t = 2(\;s)\) là
Câu 5:
Một vật dao động điều hòa theo phương trình \(x = A\cos (\omega t + \varphi )(cm)\), đại lượng \(\omega t + \varphi \) gọi là
Một vật dao động điều hòa theo phương trình \(x = A\cos (\omega t + \varphi )(cm)\), đại lượng \(\omega t + \varphi \) gọi là
Câu 6:
Con lắc đơn dao động điều hòa tại nơi có \(g = 9,81\;m/{s^2}\), với chu kì \(T = 2\;s\). Chiều dài của con lắc là
Con lắc đơn dao động điều hòa tại nơi có \(g = 9,81\;m/{s^2}\), với chu kì \(T = 2\;s\). Chiều dài của con lắc là
Câu 7:
Một con lắc lò xo có độ cứng \(k = 40\;N/m\) đang dao động điều hòa. Lúc động năng \(20\;mJ\) thì thế năng bằng \(12\;mJ\). Mốc thế năng được chọn ở vị trí cân bằng. Biên độ dao động của vật bằng
Một con lắc lò xo có độ cứng \(k = 40\;N/m\) đang dao động điều hòa. Lúc động năng \(20\;mJ\) thì thế năng bằng \(12\;mJ\). Mốc thế năng được chọn ở vị trí cân bằng. Biên độ dao động của vật bằng
Câu 8:
Con lắc lò xo đang dao động điều hòa. Khi vật nhỏ có khối lượng m, con lắc này dao động điều hoà với tần số \(f = 5\;Hz\). Khi treo vật khác có khối lượng \(m' = m - 0,15kg\) thì chu kì dao động của con lắc là \(T' = 0,1s\). Vật nhỏ có khối lượng m bằng
Câu 9:
Một con lắc đơn có độ dài \(l\), trong khoảng thời gian \(\Delta t\) nó thực hiện được \({\rm{6}}\) dao động. Người ta giảm bớt độ dài của nó đi \(28\;cm\), cũng trong thời gian \(\Delta t\) như trước nó thực hiện được 8 dao động. Chiều dài của con lắc ban đầu là
Một con lắc đơn có độ dài \(l\), trong khoảng thời gian \(\Delta t\) nó thực hiện được \({\rm{6}}\) dao động. Người ta giảm bớt độ dài của nó đi \(28\;cm\), cũng trong thời gian \(\Delta t\) như trước nó thực hiện được 8 dao động. Chiều dài của con lắc ban đầu là
Câu 10:
Một chất điểm dao động điều hoà trên trục \(Ox\). Khi đi từ vị trí biên về vị trí cân bằng thì
Một chất điểm dao động điều hoà trên trục \(Ox\). Khi đi từ vị trí biên về vị trí cân bằng thì
Câu 12:
Cơ năng của con lắc lò xo dao động điều hòa phụ thuộc vào đại lượng nào sau đây
Câu 13:
Nguồn sóng đặt tại O dao động với tần số 10 Hz. Điểm M nằm cách O đoạn 20 cm. Biết tốc độ truyền sóng là 40 cm/s. Giữa O và M có bao nhiêu điểm dao động ngược pha với nguồn?
Nguồn sóng đặt tại O dao động với tần số 10 Hz. Điểm M nằm cách O đoạn 20 cm. Biết tốc độ truyền sóng là 40 cm/s. Giữa O và M có bao nhiêu điểm dao động ngược pha với nguồn?
Câu 15:
Một vật có khối lượng \({\rm{10}}\;g\) đang dao động điều hòa với biên độ \({\rm{5}}\;cm\) và tần số góc là \({\rm{10}}rad/s\). Lực kéo về cực đại tác dụng lên vật là
Một vật có khối lượng \({\rm{10}}\;g\) đang dao động điều hòa với biên độ \({\rm{5}}\;cm\) và tần số góc là \({\rm{10}}rad/s\). Lực kéo về cực đại tác dụng lên vật là
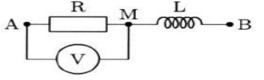
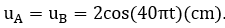Tốc độ truyền sóng trên mặt chất lỏng là 40cm/s. Gọi M là một điểm thuộc mặt chất lỏng, nằm trên đường Ax vuông góc với AB cách A một đoạn ngắn nhất mà phần tử chất lỏng tại M dao động với biên độ cực đại. Khoảng cách AM là
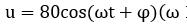không đổi và vào hai đầu đoạn mạch mắc nối tiếp theo thứ tự: điện trở R, tụ điện có điện dung C và cuộn dây thuần cảm có độ tự cảm L thay đổi được. Khi L= L1 thì điện áp giữa hai đầu cuộn dây là 
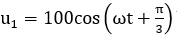. Khi L=L2 thì điện áp giữa hai đầu đoạn mạch chứa R và C là 
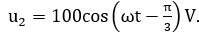Giá trị của gần nhất giá trị nào sau đây