Câu hỏi:
19/07/2024 368Cho số phức z=(4ii+1)m, m là số nguyên dương. Có bao nhiêu giá trị của m∈[1;100] để z là số thực?
A. 25.
B. 26.
C. 27.
D. 28.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án: A
Giải thích:
Lời giải:
Ta có: z=(4ii+1)m=(2+2i)m
=[(2+2i)2]m2=(8i)m2
Để z là số thực thì m2=2k⇔m=4k
Giải điều kiện 1≤4k≤100
⇔1≤k≤25(k∈ℝ)
⇒ có 25 giá trị của k nên tương ứng có 25 giá trị của m
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Tìm phần thực và phần ảo của số phức liên hợp ˉz của số phức z=−i(4i+3)
Câu 3:
Trên tập số phức, 2x + y + (2y -x)i = x - 2y + 3 + (y +2x +1)i với x, y ∈R. Tính giá trị của biểu thức P=2x+3y
Câu 4:
Cho số phức z=(2i)4-(1+i)
Câu 6:
Điểm M trong hình vẽ bên là điểm biểu diễn số phức z. Tìm phần thực và phần ảo của z.
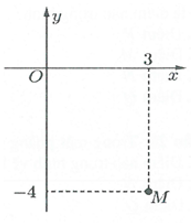
Câu 7:
Gọi M là điểm biểu diễn của số phức z, biết tập hợp các điểm M là phần tô đậm ở hình bên (kể cả biên). Mệnh đề nào sau đây đúng?
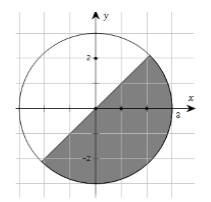
Câu 8:
Cho số phức z=(2+6i3-i)m, m là số nguyên dương. Có bao nhiêu giá trị của m∈[1;50] để z là số thuần ảo?
Câu 12:
Tìm tất cả các số thực x, y thỏa mãn đẳng thức x(3+5i)+y(1-2i)3=-35+23i
Câu 13:
Cho ba điểm A, B, C lần lượt biểu diễn các số phức sau z1=1+i;z2=z21;z3=m−i. Tìm các giá trị thực của m sao cho tam giác ABC vuông tại B
Câu 14:
Biết rằng điểm biểu diễn số phức z là điểm M ở hình bên dưới. Modun của z bằng
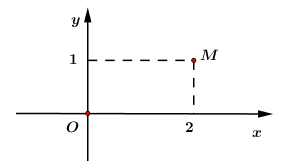
Câu 15:
Gọi A và B lần lượt là điểm biểu diễn của số phức z1=3-2i và z2=1+4i. Trung điểm của đoạn thẳng AB có tọa độ là


