Cho hình vẽ dưới đây với $\widehat{BAH }=\widehat{ACH}$.

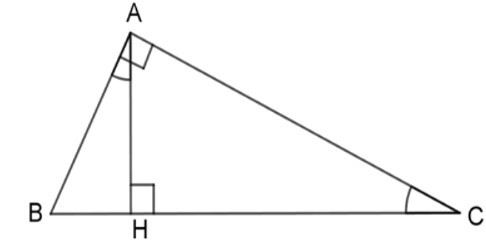
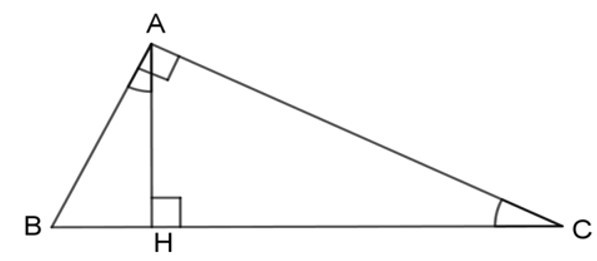
Khi đó các mệnh đề

(I) ΔAHB ~ ΔCHA (g - g)

(II) ΔAHC ~ ΔBAC (g - g)

Cho tam giác ABC vuông ở A, AB = 6cm, AC = 8cm, đường cao AH, đường phân giác BD.

1. Tính độ dài các đoạn AD, DC lần lượt là

Cho ΔDHE ~ ΔABC với tỉ số đồng dạng $\frac{2}{3}$. Có bao nhiêu khẳng định đúng trong các khẳng định sau:

(I) Tỉ số hai đường cao tương ứng của ΔDHE và ΔABC là $\frac{2}{3}$.

(II) Tỉ số hai đường cao tương ứng của ΔABC và ΔDHE là $\frac{2}{3}$.

(III) Tỉ số diện tích của ΔABC và ΔDHE là $\frac{2}{3}$.

(IV) Tỉ số diện tích của ΔDHE và ΔABC là $\frac{4}{9}$.

Cho ΔABC ~ ΔDHE với tỉ số đồng dạng $\frac{2}{3}$. Tỉ số hai đường cao tương ứng của ΔDHE và ΔABC là:

Cho tam giác ABC, phân giác AD. Gọi E, F lần lượt là hình chiếu của B và C lên AD. Chọn khẳng định không đúng.

Tam giác ABC vuông tại A có đường cao AH. Cho biết AB = 3cm; AC = 4cm. Chọn kết luận không đúng.

Cho tam giác ABC vuông tại A, đường cao AH chia cạnh BC thành hai đoạn thẳng HB = 7cm và HC = 18cm. Điểm E thuộc đoạn thẳng HC sao cho đường thẳng  đi qua E và vuông góc với BC chia tam giác ABC thành hai phần có diện tích bằng nhau. Tính CE.

Cho tam giác ABC cân tại A, AC = 20cm, BC = 24cm, các đường cao AD và CE cắt nhau ở H. Độ dài AH là:

Cho tam giác ABC cân tại A, đường cao CE. Tính AB, biết BC = 24cm và BE = 9cm.

Cho tam giác ABC vuông ở A, AB = 6cm, AC = 8cm, đường cao AH, đường phân giác BD. Gọi I là giao điểm của AH và BD.

1. Chọn kết luận đúng.

Cho các mệnh đề sau. Chọn câu đúng.

(I) Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.

(II) Nếu một góc của tam giác vuông này lớn hơn một góc của tam giác vuông kia thì hai tam giác vuông đó đồng dạng

Cho hình vẽ dưới đây với $\widehat{BAH }=\widehat{ACH}$ .

Chọn mệnh đề sai:

Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 3,5cm và HC = 9cm. Điểm E thuộc đoạn thẳng HC sao cho đường thẳng đi qua E và vuông góc với BC chia tam giác ABC thành hai phần có diện tích bằng nhau. Tính CE.

Cho tam giác ABC vuông ở A, AB = 6cm, AC = 8cm, đường cao AH, đường phân giác BD. Gọi I là giao điểm của AH và BD.

2. Chọn khẳng định đúng.

Cho tam giác ABC vuông ở A, AB = 6cm, AC = 8cm, đường cao AH, đường phân giác BD.

2. Gọi I là giao điểm của AH và BD. Chọn câu đúng.

Với giả thiết được cho trong hình, kết quả nào sau đây là đúng?