Câu hỏi:
20/07/2024 149Cho hình bình hành ABCD (AD < AB), O là giao điểm hai đường chéo AC, BD. Gọi E, F lần lượt là hình chiếu của A và C trên BD.
a) Chứng minh tứ giác AECF là hình bình hành.
b) Gọi I là điểm đối xứng của A qua BD. Chúng minh EO là đường trung bình của tam giác AIC.
c) Chứng minh tứ giác CIDB là hình thang cân.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
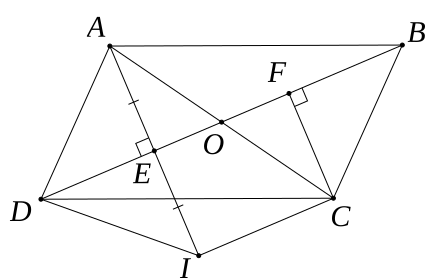
a) Hình bình hành ABCD có O là giao điểm của AC và BD
⇒ O là trung điểm của AC và BD.
⇒ OA = AC và OB = OD
Xét ΔOEA và ΔOFC có:
OA = OC
(đối đỉnh)
⇒ ΔOEA = ΔOFC (cạnh huyền – góc nhọn)
⇒ OE = OF
Xét tứ giác AECF có
OE = OF (cmt)
OA = OC (cmt)
⇒ AECF là hình bình hành (hai đường chéo cắt nhau tại trung điểm của mỗi đường)
b) I là điểm đối xứng của A qua BD
⇒ E là trung điểm của AI ⇒ AE = EI
Tam giác AIC có:
O là trung điểm của AC (cmt)
E là trung điểm của AI (cmt)
⇒ OE là đường trung bình tam giác AIC (đpcm)
⇒ OE // IC
c) Xét ΔAID có DE là đường trung trực của AI
⇒ ΔAID cân tại D
⇒ DE cũng là đường phân giác của góc ADI
mà (vì AD//BC)
Tứ giác CIDB có:
BD // IC (vì OE // IC)
⇒ Tứ giác CIBD là hình than
Mà có (cmt)
⇒ CIBD là hình thang cân. (đpcm)
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 4:
Cho tam giác ABC có MN là đường trung bình (MN//AC). Biết MN=4cm. Tính AC = ?
Câu 5:
Hình thang cân ABCD (AB//CD) có . Khẳng định nào dưới đây là đúng?
Câu 7:
Rút gọn biểu thức rồi tính giá trị của biểu thức sau:
A = (x – 3)(4x + y) – 4x(x – 3) với x = 1; .
Câu 9:
Phân tích đa thức thành nhân tử:
a) 15xy + 20xy2;
b) 4x2– y2+ 4x + 1.











