Đề thi vào 10 môn Toán Tỉnh Bắc Giang chính thức (2022) có đáp án

Chỉ 150k mua trọn bộ Đề thi vào 10 môn Toán bản word có lời giải chi tiết:

B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận giáo án.

Xem thử tài liệu tại đây: Link tài liệu

Đề thi vào 10 môn Toán Tỉnh Bắc Giang chính thức (2022 + các năm) có đáp án

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Toán vào 10

Năm học 2022 - 2023

Môn: Toán

Thời gian làm bài: 120 phút

Đề thi vào 10 môn Toán Tỉnh Bắc Giang - 2022

ĐÁP ÁN ĐỀ THI

PHẦN I. TRẮC NGHIỆM (3 điểm)

1.C	2.B	3.A	4.B	5.C	6.D	7.D	8.C	9.D	10.B
11.A	12.A	13.B	14.D	15.C	16.A	17.D	18.B	19.C	20.A

PHẦN II. TỰ LUẬN ( 7 điểm)

Câu 1 ( 2 điểm):

Lời giải

a) Giải hệ phương trình $\left\{\begin{array}{l}2\mathrm{x}+\mathrm{y}=1\\ \mathrm{x}-\mathrm{y}=2\end{array}\right.$

Ta có $\left\{\begin{array}{l}2\mathrm{x}+\mathrm{y}=1\\ \mathrm{x}-\mathrm{y}=2\end{array}\right.\iff \left\{\begin{array}{l}3\mathrm{x}=3\\ \mathrm{y}=\mathrm{x}-2\end{array}\right.\iff \left\{\begin{array}{l}\mathrm{x}=1\\ y=-1\end{array}\right.$

Vậy hệ phương trình có nghiệm (x;y)=(1;-1)

b) Rút gọn biểu thức A = $\mathrm{A}=\left(\frac{3}{\sqrt{\mathrm{x}}-2}-\frac{\sqrt{\mathrm{x}}}{\mathrm{x}-2\sqrt{\mathrm{x}}}\right):\frac{\mathrm{x}}{\sqrt{\mathrm{x}}-2}$với x > 0 và x $\ne$4

Với x > 0, x $\ne$4 ta có:

$\mathrm{A}=\left(\frac{3}{\sqrt{\mathrm{x}}-2}-\frac{\sqrt{\mathrm{x}}}{\mathrm{x}-2\sqrt{\mathrm{x}}}\right):\frac{\mathrm{x}}{\sqrt{\mathrm{x}}-2}$

$\mathrm{A}=\left(\frac{3}{\sqrt{\mathrm{x}}-2}-\frac{\sqrt{\mathrm{x}}}{\sqrt{\mathrm{x}}(\sqrt{\mathrm{x}}-2)}\right).\frac{\sqrt{\mathrm{x}}-2}{\mathrm{x}}$

$\mathrm{A}=\left(\frac{3}{\sqrt{\mathrm{x}}-2}-\frac{1}{(\sqrt{\mathrm{x}}-2)}\right).\frac{\sqrt{\mathrm{x}}-2}{\mathrm{x}}$

$\mathrm{A}=\frac{2}{\sqrt{\mathrm{x}}-2}.\frac{\sqrt{\mathrm{x}}-2}{\mathrm{x}}$

$\mathrm{A}=\frac{2}{\mathrm{x}}$

Vậy với x > 0, x $\ne$4 thì $\mathrm{A}=\frac{2}{\mathrm{x}}$

Câu 2 ( 1,0 điểm):

Lời giải

Cho phương trình x² - 2mx - 9 = 0 (1), m là tham số

a) Giải phương trình (1) khi m = 4.

Với m = 4, thay vào phương trình 91), ta được: x² - 8x - 9 = 0

Ta có $∆\text{'}={(-4)}^2+9=25>0$

$\Rightarrow$Phương trình có hai nghiệm phân biệt $\left[\begin{array}{c}\mathrm{x}=4+\sqrt{25}=9\\ \mathrm{x}=4-\sqrt{25}=-1\end{array}\right.$

Vậy với m = 4, phương trình có tập nghiệm là S = { -1; 9}

b) Tìm tất cả các giá trị của m để phương trình (1) có hai nghiệm phân biệt x₁, x₂ thoả mãn x₁³ + 9x₂ = 0

Ta có: $∆\text{'}={(=\mathrm{m})}^2-(-9)={\mathrm{m}}^2+9>0,\forall \mathrm{m}$

$\Rightarrow$Phương trình (1) luôn có hai nghiệm phân biệt x₁, x₂ với mọi m

Theo hệ thức Vi - ét, ta có : $\left\{\begin{array}{l}{\mathrm{x}}_1+{\mathrm{x}}_2=2\mathrm{m} \left(1\right)\\ {\mathrm{x}}_1.{\mathrm{x}}_2=-9 \left(2\right)\end{array}\right.$

Theo giả thiết ta có: x₁³ + 9x₂ = 0 $\iff {\mathrm{x}}_2=-\frac{{\mathrm{x}}_1^3}{9}$

Thay vào (2) ta có: ${\mathrm{x}}_1.\frac{-{\mathrm{x}}_1^3}{9}=-9\iff {\mathrm{x}}_1^4=81\iff {\mathrm{x}}_1^2=9$

$\iff \left\{\begin{array}{l}{\mathrm{x}}_1=3\Rightarrow {\mathrm{x}}_2=-3\\ {\mathrm{x}}_1=-3\Rightarrow {\mathrm{x}}_2=3\end{array}\right.\Rightarrow {\mathrm{x}}_1+{\mathrm{x}}_2=0$

Thay vào (1) ta có: 0 = 2m $\iff$m = 0.

Vậy m = 0.

Câu 3 (1,5 điểm):

Lời giải

Ban đầu khán đài của Nhà thi đáu các nội dung thuộc bộ môn Bơi tại SEA Games chứa 1188 ghế được xếp thành các dãy, số lượng ghế ở các dãy bằng nhau. Để phục vụ đông đảo khán giả hơn, khán đài sau đó đã được lắp thêm 2 dãy ghế và mỗi dãy được lắp thêm 4 ghế. Vì thế, khán đài được tăng thêm 254 ghế. Tìm số dãy ghế ban đầu của khán đài.

Gọi số dãy ghế ban đầu của khán đài là x ( dãy) ( x$\in \mathrm{\mathbb{N}}*$)

số ghế mỗi dãy ban đầu là y ( y$\in \mathrm{\mathbb{N}}*$)

Vì ban đầu, khán đài của Nhà thi đấu các nội dung thuộc môn Bơi tại SEA Games chưa 1188 ghế nên ta có phương trình: xy = 1188 (1)

Lúc sau:

Số dãy ghế là: x + 2 ( dãy)

Số ghế ở mỗi dãy là: y + 4 (ghế)

Vì lúc sau, khán đài được tăng thêm 254 ghế nên ta có phương trình:

(x + 2)(y + 4) = xy + 254 (2)

Từ (1) và (2) ta có hệ phương trình:

 $$\begin{gathered} \left\{\begin{array}{l}\mathrm{xy} = 1188\\ (\mathrm{x}+2)( \mathrm{y}+4) = \mathrm{xy}+254 \end{array}\right. \\ \iff \left\{\begin{array}{l}\mathrm{xy} = 1188\\ \mathrm{xy}+4\mathrm{x}+2\mathrm{y}+8=\mathrm{xy}+254\end{array}\right. \end{gathered}$$

$$\begin{gathered} \iff \left\{\begin{array}{l}\mathrm{xy} = 1188\\ 4\mathrm{x}+2\mathrm{y}=246\end{array}\right. \\ \iff \left\{\begin{array}{l}\mathrm{xy} = 1188\\ 2\mathrm{x}+\mathrm{y}=123\end{array}\right. \\ \iff \left\{\begin{array}{l}\mathrm{xy} = 1188\\ \mathrm{y}=123-2\mathrm{x}\end{array}\right. \\ \iff \left\{\begin{array}{l}\mathrm{x}(123-2\mathrm{x})= 1188\\ \mathrm{y}=123-2\mathrm{x}\end{array}\right. \\ \iff \left\{\begin{array}{l}2{\mathrm{x}}^2-123\mathrm{x}+1188=0 (*)\\ \mathrm{y}=123-2\mathrm{x}\end{array}\right. \end{gathered}$$

Giải hệ phương trình (*) ta có: $∆$= 123² - 4.2.1188 = 5625 > 0, $\sqrt{∆}$=75 nên phương trình có 2 nghiệm phân biệt 

$\left[\begin{array}{c}{\mathrm{x}}_1=\frac{123+75}{2.2}=\frac{99}{2} \left(\mathrm{KTM}\right)\\ {\mathrm{x}}_2=\frac{123-75}{2.2}=12 \left(\mathrm{TM}\right) \end{array}\right.$

Vậy số dãy ghế ban đầu của khán đài là 12 dãy.

Câu 4 (2,0 điểm):

Lời giải

Cho đường tròn (O) đường kính AB, bán kính OC vuông góc với AB. Gọi H là trung điểm của đoạn thẳng BC. Đường thẳng AB cắt OC tại D và cắt đường tròn (O) tại điểm thứ hai là K ( K khác A).

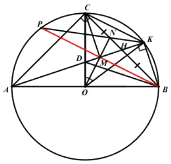a) Chứng minh tứ giác ODKB nội tiếp một đường tròn

Xét (O) có: K thuộc đường tròn nên $\stackrel{⏜}{\mathrm{AKB}}=90°$( góc nội tiếp chắn nửa đường tròn bằng 90^o)

$\Rightarrow \stackrel{⏜}{\mathrm{DKB}}=90°$

$\Rightarrow ∆\mathrm{BDK}$ vuông tại K

$\Rightarrow$K thuộc đường tròn bán kính BD (1)

Ta có: OC$\perp$AB tại O (gt) $\Rightarrow$$\stackrel{⏜}{\mathrm{BOC}}=90°\Rightarrow \stackrel{⏜}{\mathrm{BOD}}=90°$

$\Rightarrow △\mathrm{OBD}$vuông tại O

$\Rightarrow$O thuộc đường tròn bán kính BD (2)

Từ (1) và (2), suy ra O, K thuộc đường tròn đường kính BD

Vậy tứ giác ODKB nội tiếp đường tròn.

b) Tia phân giác của góc COK cắt AK tại M . Chứng mình góc CMA = 90^o

Xét tam giác COK có: OC = OK $\Rightarrow △\mathrm{COK}$ cân tại O

$\Rightarrow \stackrel{⏜}{\mathrm{OCK}}=\stackrel{⏜}{\mathrm{CKO}}$

Lại có: ON là tia phân giác của $\stackrel{⏜}{\mathrm{COK}} \left(\mathrm{gt}\right)$

$\Rightarrow$ON đồng thời là đường trung trực của $△$COK

Mà M$\in$ON$\Rightarrow$CM = MK ( tính chất đường trung trực)

$\Rightarrow △$CMK cân tại M $\Rightarrow \stackrel{⏜}{\mathrm{MCK}}=\stackrel{⏜}{\mathrm{CKM}}$

Ta có:

$\stackrel{⏜}{\mathrm{OCK}}=\stackrel{⏜}{\mathrm{CKO}} \left(\mathrm{cmt}\right)$

$$\begin{gathered} \Rightarrow \stackrel{⏜}{\mathrm{OCM}}+\stackrel{⏜}{\mathrm{CMK}}=\stackrel{⏜}{\mathrm{OKM}}+\stackrel{⏜}{\mathrm{MKC}} \\ \Rightarrow \stackrel{⏜}{\mathrm{OCM}}=\stackrel{⏜}{\mathrm{OKM}} (\hspace{0.17em}\mathrm{do} \stackrel{⏜}{\mathrm{MCK}}=\stackrel{⏜}{\mathrm{CKM} }(\mathrm{cmt}) \\ \Rightarrow \stackrel{⏜}{\mathrm{OCM}}=\stackrel{⏜}{\mathrm{DKO}} (3) \end{gathered}$$

Tứ giác DKBO nội tiếp đường tròn 

$\Rightarrow$$\stackrel{⏜}{\mathrm{DKO}}=\stackrel{⏜}{\mathrm{DBO}}$ ( 2 góc nội tiếp cùng chắn cung OD) (4)

Từ (3) và (4), suy ra $\stackrel{⏜}{\mathrm{OCM}}=\stackrel{⏜}{\mathrm{DBO}}$

Tam giác ABD có:

+ DO là đường cao ( do OC vuông góc với AB tại O)

+ DO là đường trung tuyến ( do O là tâm đường tròn đường kính AB nên O là trung điểm AB)

$\Rightarrow △\mathrm{ABD}$ cân tại D

$$\begin{gathered} \Rightarrow \stackrel{⏜}{\mathrm{DAO}}=\stackrel{⏜}{\mathrm{DBO}} \\ \Rightarrow \stackrel{⏜}{\mathrm{MAO}}=\stackrel{⏜}{\mathrm{DBO}} \end{gathered}$$

Mà $\stackrel{⏜}{\mathrm{OCM}}=\stackrel{⏜}{\mathrm{DBO}} \left(\mathrm{cmt}\right)$

$\Rightarrow \stackrel{⏜}{\mathrm{MAO}}=\stackrel{⏜}{\mathrm{OCM}}$

Xét tứ giác AOMC có: $\stackrel{⏜}{\mathrm{MAO}}=\stackrel{⏜}{\mathrm{OCM}}$ mà hai góc này có đỉnh kề nhau cùng chắn cung AC

$\Rightarrow \mathrm{AOMC}$ là tứ giác nội tiếp (dhnb)

$\Rightarrow \stackrel{⏜}{\mathrm{AOC}}=\stackrel{⏜}{\mathrm{AMC}}$

Mà $\stackrel{⏜}{\mathrm{AOC}}=90°$ ( do AB vuông góc với CO tại O)

$\Rightarrow \stackrel{⏜}{\mathrm{AMC}}=90°$ (đpcm)

c) Áp dụng hệ thức lượng trong tam giác vuông AHC có: HM.HA = HC² = HB²

$\Rightarrow \frac{\mathrm{HM}}{\mathrm{HB}}=\frac{\mathrm{HB}}{\mathrm{HA}}$

Xét $△\mathrm{HBM} \mathrm{va} △\mathrm{HAB}$ có:

$\stackrel{⏜}{\mathrm{AHB}} \mathrm{chung}$

$\frac{\mathrm{HM}}{\mathrm{HB}}=\frac{\mathrm{HB}}{\mathrm{HA}} \left(\mathrm{cmt}\right)$

$$\begin{gathered} \Rightarrow △\mathrm{HBM} - △\mathrm{HAB} ( \mathrm{c}.\mathrm{g}.\mathrm{c}) \\ \Rightarrow \stackrel{⏜}{\mathrm{HAB}}=\stackrel{⏜}{\mathrm{HBM} }( 2 \mathrm{góc} \mathrm{tương} \mathrm{ứng}) \end{gathered}$$

Mà $\stackrel{⏜}{\mathrm{HAB}}=\stackrel{⏜}{\mathrm{KPB}}$ ( 2 góc nội tiếp cùng chắn cung KB)

$\Rightarrow \stackrel{⏜}{\mathrm{KBP}}=\stackrel{⏜}{\mathrm{HBM}} \mathrm{hay} \stackrel{⏜}{\mathrm{NPB}}=\stackrel{⏜}{\mathrm{NBP}}$

$\Rightarrow \stackrel{⏜}{\mathrm{NBP}}$ cân tại N ( tam giác có 2 góc ở đáy bằng nhau) $\Rightarrow$NP=NB(tính chất tam giác cân)

Xét $△$ONB và $△$ONP có:

OB = OP ( = R)

ON chung

NB = NP ( cmt)

$\Rightarrow △\mathrm{ONB} = △\mathrm{ONP} (\hspace{0.17em}\mathrm{c}.\mathrm{c}.\mathrm{c})$

$\Rightarrow \stackrel{⏜}{\mathrm{NOB}}=\stackrel{⏜}{\mathrm{NOB}}$ ( 2 góc tương ứng) $\Rightarrow$ON là phân giác của $\stackrel{⏜}{\mathrm{BOP}}\Rightarrow$OMlà phân giác của $\stackrel{⏜}{\mathrm{BOP}}$

Xét tam giác OBP có: OB = OP ( = R) nên $△\mathrm{OBP}$ cân tại O $\Rightarrow$phân giác OM đồng thời là đường trung tuyến.

$\Rightarrow$M là trung điểm của BP.

Vậy B đối xứng P qua M ( đpcm)

Câu 5 ( 0,5 điểm):

Lời giải

Cho các số a, b thoả mãn $( 1+ \mathrm{a})( 1- \mathrm{b}) \ge \frac{9}{4}$. Tìm giá trị nhỏ nhất của biểu thức P = a² + 2b² + b.

Sử dụng BĐT $\mathrm{xy} \le \frac{{(\mathrm{x}+\mathrm{y})}^2}{4}$ ta có $(1+\mathrm{a})(1-\mathrm{b})\le \frac{{(\mathrm{a}-\mathrm{b}+2)}^2}{4}$

$$\begin{gathered} \iff \frac{{(\mathrm{a}-\mathrm{b}+2)}^2}{4}\ge \frac{9}{4} \\ \iff \mathrm{a}-\mathrm{b}+2\ge 3 \\ \iff \mathrm{a}\ge \mathrm{b}+1 \end{gathered}$$

Thay vào P ta được:

P = a² + 2b² + b $\ge$(b+1)² + 2b² + b

$\iff$P$\ge$b² + 2b + 1 + 2b² + b

$\iff$P$\ge$3b² + 3b + 1

Ta có:

3b² + 3b + 1

= 3(b² + b) + 1

= 3$\left({\mathrm{b}}^2+2\mathrm{b}\frac{1}{2}+\frac{1}{4}\right)-\frac{3}{4}+1$

= 3${\left(\mathrm{b}+\frac{1}{2}\right)}^2+\frac{1}{4}\ge \frac{1}{4}\forall \mathrm{b}$

$\Rightarrow \mathrm{P}\ge \frac{1}{4}$

Dấu " =" xảy ra khi

 $\left\{\begin{array}{l}1+\mathrm{a}=1-\mathrm{b}\\ \mathrm{a}=\mathrm{b}+1\\ \mathrm{b}+\frac{1}{2}=0\end{array}\right.\iff \left\{\begin{array}{l}\mathrm{a}=-\mathrm{b}\\ \mathrm{a}=\mathrm{b}+1\\ \mathrm{b}=-\frac{1}{2}\end{array}\right.\iff \left\{\begin{array}{l}\mathrm{a}=\frac{1}{2}\\ \mathrm{b}=-\frac{1}{2}\end{array}\right.$

Vậy P đạt giá trị nhỏ nhất bằng $\frac{1}{4}$khi a = $\frac{1}{2}$; b = $-\frac{1}{2}$