Sau bài học này, ta giải quyết được bài toán này như sau:

Gọi biến cố A: “Hạt thứ nhất nảy mầm”.

Biến cố B: “Hạt thứ hai nảy mầm”.

Ta có A, B là hai biến cố độc lập và P(A) = P(B) = 0,8, suy ra $P\left(\overline{A}\right)=P\left(\overline{B}\right)=0,2$.

Do A, B độc lập nên A, $\overline{B}$ và $\overline{A}$, B cũng độc lập.

Xác suất của biến cố: “Có đúng 1 trong 2 hạt giống đó nảy mầm” là

$P(A\overline{B}\cup \overline{A}B)=P\left(A\overline{B}\right)+P\left(\overline{A}B\right)=P\left(A\right)P\left(\overline{B}\right)+P\left(\overline{A}\right)P\left(B\right)$ = 0,8×0,2 + 0,2×0,8 = 0,32.

Vậy xác suất để có đúng 1 trong 2 hạt giống đó nảy mầm là 0,32.

Không gian mẫu W = {(i; j)| 1 ≤ i ≤ 5; 1 ≤ j ≤ 5; i ≠ j}.

Ta có: A = {(2; 1); (2; 3); (2; 4); (2; 5); (4; 1); (4; 2); (4; 3); (4; 5)}.

B = {(1; 2); (3; 2); (4; 2); (5; 2); (1; 4); (2; 4); (3; 4); (5; 4)}.

C = {(1; 2); (1; 4); (2; 1); (2; 3); (2; 4); (2; 5); (3; 2); (3; 4); (4; 1); (4; 2); (4; 3); (4; 5); (5; 2); (5; 4)}.

a) Số kết quả thuận lợi cho biến cố A là: $C_{17}^3=680$.

Số kết quả thuận lợi cho biến cố B là: $C_{17}^2\cdot C_{15}^1=2040$.

b) A $\cup$ B là biến cố: “Có ít nhất 2 học sinh nữ trong 3 học sinh được chọn”.

Số kết quả thuận lợi cho biến cố A $\cup$ B là:

$C_{17}^3+C_{17}^2\cdot C_{15}^1$ = 680 + 2 040 = 2 720.

Gọi biến cố A: "Lá bài được chọn có màu đỏ hoặc là lá có số chia hết cho 5".

Rút ngẫu nhiên 1 lá bài từ bộ bài tây 52 lá có 52 cách, suy ra n(W) = 52.

Lá bài có màu đỏ hoặc lá có số chia hết cho 5 có 30 lá, suy ra n(A) = 30.

Do đó, $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{30}{52}=\frac{15}{26}$.

Vậy xác suất để lá bài được chọn có màu đỏ hoặc là lá có số chia hết cho 5 là $\frac{15}{26}$.

Vì A, B độc lập với nhau nên P(AB) = P(A)P(B) = 0,9×0,6 = 0,54.

Ta có P(A $\cup$ B) = P(A) + P(B) – P(AB) = 0,9 + 0,6 – 0,54 = 0,96.

Vậy P(A $\cup$ B) = 0,96.

Gọi biến cố A: “Học sinh đó thuận tay trái”.

Biến cố B: “Học sinh đó bị cận thị”.

Biến cố AB: “Học sinh đó bị cận thị và thuận tay trái”.

Biến cố A $\cup$ B: “Học sinh đó bị cận thị hoặc thuận tay trái”.

Theo đề ta có: P(A) = 20%; P(B) = 35%.

Vì A, B độc lập nên P(AB) = P(A)P(B) = 20%×35% = 7%.

Ta có P(A $\cup$ B) = P(A) + P(B) – P(AB) = 20% + 35% − 7% = 48%.

Vậy xác suất để học sinh đó bị cận thị hoặc thuận tay trái là 48%.

Số cách chọn ngẫu nhiên từ hộp 3 quả bóng là $C_{13}^3=286$ (cách).

a) Gọi biến cố A: “3 quả bóng lấy ra là màu xanh” và biến cố B: “3 quả bóng lấy ra là màu đỏ”.

A $\cup$ B là biến cố: “Cả 3 quả bóng lấy ra đều có cùng màu”.

Vì A và B xung khắc nên P(A È B) = P(A) + P(B).

Ta có $P\left(A\right)=\frac{C_5^3}{C_{13}^3}=\frac{10}{286}=\frac{5}{143}$; $P\left(B\right)=\frac{C_6^3}{C_{13}^3}=\frac{20}{286}=\frac{10}{143}$.

Do đó $P\left(A\cup B\right)=\frac{5}{143}+\frac{10}{143}=\frac{15}{143}$.

Vậy xác suất để 3 quả bóng lấy ra đều có cùng màu là $\frac{15}{143}$.

b) Gọi biến cố D: “Lấy được 2 quả bóng màu xanh”.

Khi đó biến cố A $\cup$ D: “Có ít nhất 2 quả bóng xanh trong 3 quả bóng lấy ra”.

Vì A và D xung khắc nên P(A $\cup$ D) = P(A) + P(D).

Có $P\left(D\right)=\frac{C_5^2{C}_8^1}{C_{13}^3}=\frac{40}{143}$.

Do đó $P\left(A\cup D\right)=\frac{5}{143}+\frac{40}{143}=\frac{45}{143}.$

Vậy xác suất để có ít nhất 2 quả bóng xanh trong 3 quả bóng lấy ra là $\frac{45}{143}$.

Số phần tử không gian mẫu là 7!.

Gọi A là biến cố “Bình vẫn ngồi đúng ghế cũ của mình” và B là biến cố “Minh vẫn ngồi đúng ghế cũ của mình”.

AB là biến cố: “Cả hai bạn Bình và Minh vẫn ngồi đúng ghế cũ của mình”.

A È B là biến cố “Có ít nhất một trong hai bạn Bình và Minh vẫn ngồi đúng ghế cũ của mình”.

Xác suất để Bình vẫn ngồi đúng ghế cũ của mình là: $P\left(A\right)=\frac{6!}{7!}=\frac{1}{7}$.

Xác suất để Minh vẫn ngồi đúng ghế cũ của mình là: $P\left(B\right)=\frac{6!}{7!}=\frac{1}{7}$.

Xác suất để cả hai bạn Bình, Minh vẫn ngồi đúng ghế cũ của mình là:

$P\left(AB\right)=\frac{5!}{7!}=\frac{1}{42}$.

Xác suất để có ít nhất một trong hai bạn Bình và Minh vẫn ngồi đúng ghế cũ của mình là:

P(A È B) = P(A) + P(B) – P(AB) = $\frac{1}{7}+\frac{1}{7}-\frac{1}{42}=\frac{11}{42}$.

Vậy xác suất để có ít nhất một trong hai bạn Bình và Minh vẫn ngồi đúng ghế cũ của mình là $\frac{11}{42}$.

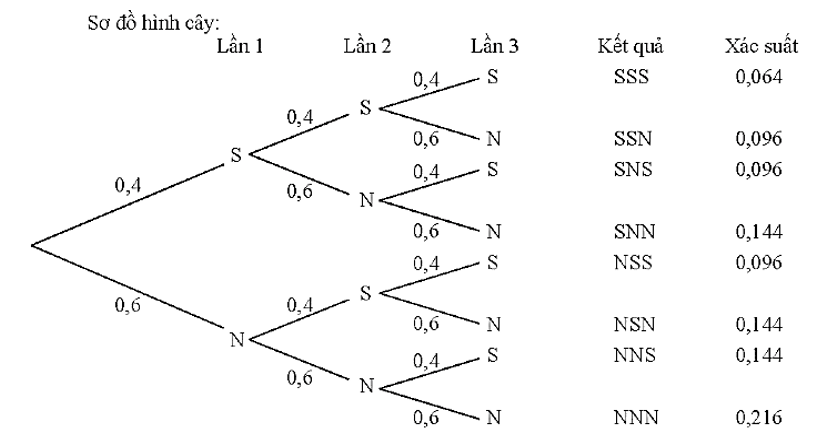
Theo sơ đồ hình cây trên, xác suất để có đúng 1 lần gieo được mặt sấp trong 3 lần gieo là:

0,144 + 0,144 + 0,144 = 0,432.

Vậy xác suất để có đúng 1 lần gieo được mặt sấp trong 3 lần gieo là 0,432.