Giải SBT Vật lý 11 KNTT Sự truyền năng lượng của sóng cơ
Giải SBT Vật lý 11 KNTT Sự truyền năng lượng của sóng cơ
-
97 lượt thi
-
11 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
20/07/2024Chọn câu đúng.
A. Sóng dọc là sóng truyền dọc theo một sợi dây.
B. Sóng dọc là sóng truyền theo phương thẳng đứng, còn sóng ngang là sóng truyền theo phương nằm ngang.
C. Sóng dọc là sóng trong đó phương dao động (của các phần tử môi trường) trùng với phương truyền.
D. Sóng ngang là sóng trong đó phương dao động (của các phần tử môi trường) trùng với phương truyền.
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Sóng dọc là sóng trong đó phương dao động (của các phần tử môi trường) trùng với phương truyền.
Câu 2:
22/07/2024Tìm phát biểu sai khi nói về sóng cơ.
A. Bước sóng là khoảng cách giữa hai điểm gần nhau nhất trên cùng một phương truyền sóng dao động ngược pha nhau.
B. Sóng trong đó các phần tử môi trường dao động theo phương trùng với phương truyền sóng được gọi là sóng dọc.
C. Tại mỗi điểm của môi trường có sóng truyền qua, biên độ của sóng là biên độ dao động của phần tử môi trường.
D. Sóng trong đó các phần tử môi trường dao động theo phương vuông góc với phương truyền sóng được gọi là sóng ngang.
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Bước sóng là khoảng cách giữa hai điểm gần nhau nhất trên cùng một phương truyền sóng dao động cùng pha nhau.
Câu 3:
22/07/2024Sóng cơ không truyền được trong
A. chân không.
B. không khí.
C. nước.
D. kim loại.
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Sóng cơ không truyền được trong chân không.
Câu 4:
21/07/2024Một sóng ngang có tần số \(100{\rm{\;Hz}}\) truyền trên một sợi dây nằm ngang với tốc độ \(60{\rm{\;m}}/{\rm{s}}\), qua điểm \(A\) rồi đến điểm \(B\) cách nhau \(7,95{\rm{\;m}}\). Tại một thời điểm nào đó \(A\) có li độ âm và đang chuyển động đi lên thì điểm \(B\) đang có li độ
A. âm và đang đi xuống.
B. âm và đang đi lên.
C. dương và đang đi lên.
D. dương và đang đi xuống Xem đáp án
Xem đáp án
Đáp án đúng là A
Sử dụng đồ thị li độ quãng đường Hình 9.1G của sóng quy ước chiều truyền dương để xác định các vùng mà các phần tử vật chất đang đi lên và đi xuống.
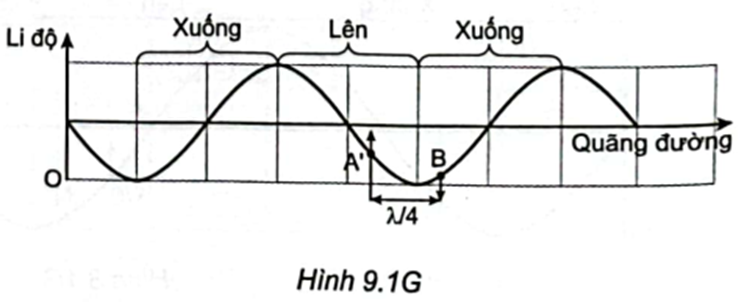
Ta có: \(\lambda = \frac{v}{f} = \frac{{60}}{{100}} = 0,6{\rm{\;m}};AB = 7,95{\rm{\;m}} = 7,8 + 0,15 = 13 \cdot 0,6 + 0,15 = 13\lambda + \frac{\lambda }{4}\).
Từ Hình 9.1G. Ta thấy B có li độ âm và đang đi xuống.
Câu 5:
22/07/2024Mũi tên nào trong Hình 9.1. mô tả đúng hướng truyền dao động của các phần tử môi trường?
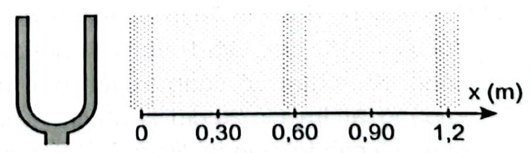
A. \( \uparrow \).
B. \( \downarrow \).
C. \( \to \).
D. \( \leftrightarrow \).
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Dựa vào hình vẽ thấy đấy là sóng dọc, chiều của trục toạ độ từ trái sáng phải.
Câu 6:
21/07/2024Nếu tốc độ truyền sóng âm trong Hình 9.1 là \(340{\rm{\;m}}/{\rm{s}}\) thì tần số của sóng khoảng
A. \(566,7{\rm{\;Hz}}\).
B. \(204{\rm{\;Hz}}\).
C. \(0,00176{\rm{\;Hz}}\).
D. 0,176 Hz.
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Từ hình vẽ thấy bước sóng là 0,6 m nên tần số là \[f = \frac{v}{\lambda } = \frac{{340}}{{0,6}} = 566,7\,Hz\]
Câu 7:
08/07/2024Một sóng ngang truyền trên một sợi dây rất dài từ \(P\) đến \(Q\). Hai điểm \(P,Q\) trên phương truyền sóng cách nhau \(PQ = \frac{{5\lambda }}{4}\). Kết luận nào sau đây là đúng?
A. Khi \(P\) có li độ cực đại thì \(Q\) có vận tốc cực đại.
B. Li độ \(P,Q\) luôn trái dấu.
C. Khi \(Q\) có li độ cực đại thì \(P\) có vận tốc cực đại.
D. Khi \(P\) có li độ cực đại thì \(Q\) qua vị trí cân bằng theo chiều âm. Khi \(Q\) có li độ cực đại thì \({\rm{P}}\) qua vị trí cân bằng theo chiều dương.
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Sử dụng đồ thị li độ - quãng đường Hình 9.2Ga, b.
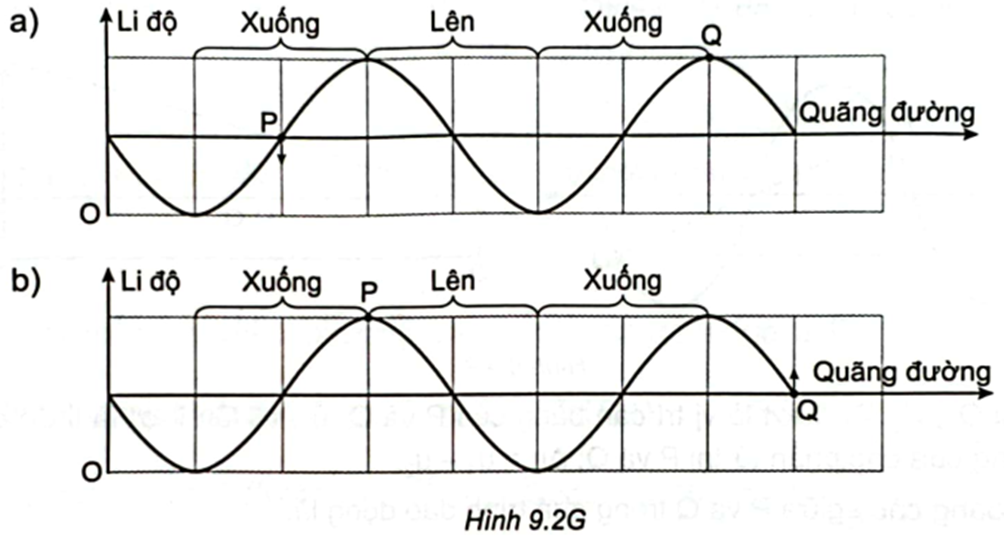
Ta thấy theo Hình 9.2Ga, khi Q có li độ cực đại thì P qua vị trí cân bằng theo chiều âm; theo Hình 9.2Gb thì khi P có li độ cực đại thì Q qua vị trí cân bằng theo chiều dương.
Câu 8:
23/07/2024Một sóng cơ có tần số \(20{\rm{\;Hz}}\) truyền trên mặt nước với tốc độ \(1,5{\rm{\;m}}/{\rm{s}}\). Trên phương truyền sóng, sóng truyền tới điểm \({\rm{P}}\) rồi mới tới điểm \(Q\) cách nó \(16,125{\rm{\;cm}}\). Tại thời điểm \({\rm{t}}\), điểm \({\rm{P}}\) hạ xuống thấp nhất thì sau thời gian ngắn nhất là bao nhiêu điểm \(Q\) sẽ hạ xuống thấp nhất?
 Xem đáp án
Xem đáp án
Ta có: \(\lambda = \frac{v}{f} = \frac{{1,5}}{{20}} = 0,075{\rm{\;m}} = 7,5{\rm{\;cm}}\)
\(PQ = 16,125{\rm{\;cm}} = 2\lambda + 0,15\lambda = Q'Q + PQ'\)

Kết hợp với sử dụng đồ thị Hình 9.3G ta thấy thời gian ngắn nhất để Q' đi từ vị trí hiện tại đến vị trí thấp nhất là \(0,15{\rm{\;T}} = \frac{{0,15}}{{20}} = \frac{3}{{400}}{\rm{\;s}}\).
Câu 9:
21/07/2024Hình 9.2 mô tả một phần của sóng dọc truyền trên một sợi dây lò xo. Hãy nêu cách xác định bước sóng của sóng này và chỉ ra điểm tương đồng của nó với sóng âm truyền trong không khí.

Hình 9.2.
 Xem đáp án
Xem đáp án
- Xác định bước sóng bằng khoảng cách giữa hai tâm nén gần nhau nhất.
- Điểm tương đồng giữa sóng nén, dãn trên dây lò xo và sóng âm truyền trong không khí là: đều là sóng dọc (có phương dao động trùng với phương truyền sóng; đều truyền năng lượng, lan truyền sự nén, dãn theo phương truyền sóng,...
Câu 10:
18/07/2024\(P\) và \(Q\) là hai điểm trên mặt nước cách nhau một khoảng \(20{\rm{\;cm}}\). Tại một điểm \({\rm{O}}\) trên đường thẳng \({\rm{PQ}}\) và nằm ngoài đoạn \({\rm{PQ}}\), người ta đặt nguồn dao động điều hoà theo phương vuông góc với mặt nước với phương trình \({\rm{u}} = 5{\rm{cos}}\omega {\rm{t}}\left( {{\rm{cm}}} \right)\), tạo ra sóng trên mặt nước với bước sóng \(\lambda = 15{\rm{\;cm}}\). Khoảng cách xa nhất và gần nhất giữa hai phần tử môi trường tại \({\rm{P}}\) và \(Q\) khi có sóng truyền qua là bao nhiêu?
 Xem đáp án
Xem đáp án
Đối với trường hợp sóng ngang, khoảng cách giữa hai điểm P, Q khi dao động được mô tả như Hình 9.4G.
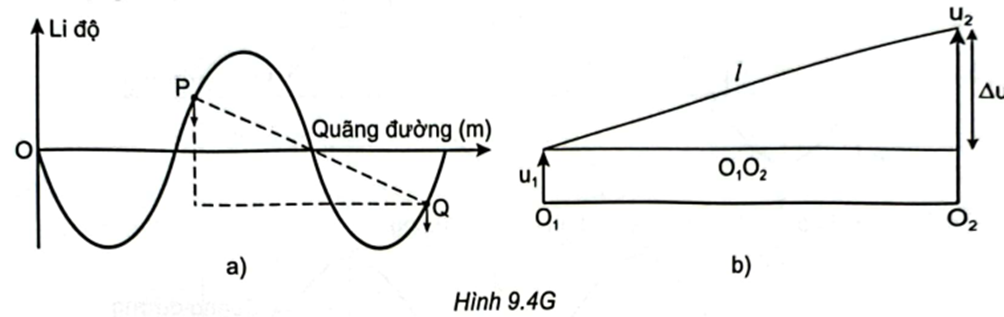
Gọi O1, O2 lần lượt là vị trí cân bằng của P và Q; u1, u2 lần lượt là li độ dao động của các phần tử tại P và Q;\({\rm{\Delta }}u = {u_1} - {u_2}\).
Khoảng cách giữa P và Q trong quá trình dao động là:
\(l = \sqrt {{{\left( {{{\rm{O}}_1}{{\rm{O}}_2}} \right)}^2} + {{({\rm{\Delta u}})}^2}} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{l_{{\rm{min}}}} = \sqrt {{{\left( {{{\rm{O}}_1}{{\rm{O}}_2}} \right)}^2} + {{(0)}^2}} = {{\rm{O}}_1}{{\rm{O}}_2}}\\{{l_{{\rm{max}}}} = \sqrt {{{\left( {{{\rm{O}}_1}{{\rm{O}}_2}} \right)}^2} + {{\left( {{\rm{\Delta }}{{\rm{u}}_{{\rm{max}}}}} \right)}^2}} }\end{array}} \right.\)
Vậy khoảng cách gần nhất giữa P và Q là: \({l_{{\rm{min}}}} = {O_1}{O_2} = 20{\rm{\;cm}}\).
Khoảng cách xa nhất giữa P và Q là: \({l_{{\rm{max}}}} = \sqrt {{{\left( {{{\rm{O}}_1}{{\rm{O}}_2}} \right)}^2} + {{\left( {{\rm{\Delta }}{{\rm{u}}_{{\rm{max}}}}} \right)}^2}} \).
Giả sử sóng truyền qua P rồi mới đến Q thì dao động tại P sớm pha hơn Q là: \({\rm{\Delta }}\varphi = \frac{{2\pi \left( {PQ} \right)}}{\lambda } = \frac{{8\pi }}{3}\)
Chọn mốc thời gian để phương trình dao động của phần tử tại P là: \({u_1} = 5{\rm{cos}}\omega t\left( {{\rm{cm}}} \right)\)
thì phương trình dao động của phần tử tại Q là: \({u_2} = 5{\rm{cos}}\left( {\omega t - \frac{{8\pi }}{3}} \right)\left( {{\rm{cm}}} \right)\).
\({\rm{\Delta u}} = {{\rm{u}}_1} - {{\rm{u}}_2} = 5{\rm{cos}}\left( {\omega {\rm{t}} - \frac{{8\pi }}{3}} \right) - 5{\rm{cos}}\omega {\rm{t}} = 5\sqrt 3 {\rm{cos}}\left( {\omega {\rm{t}} - \frac{{5\pi }}{6}} \right)\left( {{\rm{cm}}} \right)\)
\( \Rightarrow {\rm{\Delta }}{{\rm{u}}_{{\rm{max}}}} = 5\sqrt 3 {\rm{\;cm}}\).
\({l_{{\rm{max}}}} = \sqrt {{{(20)}^2} + {{(5\sqrt 3 )}^2}} = 5\sqrt {19} {\rm{\;cm}}.\)
Câu 11:
18/07/2024Một sóng dọc truyền trong môi trường với bước sóng \(15{\rm{\;cm}}\), biên độ không đổi \(A = 5\sqrt 3 {\rm{\;cm}}\). Gọi \(P\) và \(Q\) là hai điểm cùng nằm trên một phương truyền sóng. Khi chưa có sóng truyền đến hai điểm \(P\) và \(Q\) nằm cách nguồn các khoảng lần lượt là \(20{\rm{\;cm}}\) và \(30{\rm{\;cm}}\). Khoảng cách xa nhất và gần nhất giữa hai phần tử môi trường tại \({\rm{P}}\) và \({\rm{Q}}\) khi có sóng truyền qua là bao nhiêu?
 Xem đáp án
Xem đáp án
Đối với trường hợp sóng dọc, khoảng cách giữa hai điểm P, Q khi dao động được mô tả như Hình 9.5G.

Gọi O1, O2 lần lượt là vị trí cân bằng của \({\rm{P}}\) và Q; u1, u2 lần lượt là li độ dao động của các phần tử tại P và Q;\({\rm{\Delta }}u = {u_1} - {u_2}\).
Khoảng cách giữa P và Q trong quá trình dao động là:
\(l = {{\rm{O}}_1}{{\rm{O}}_2} + {\rm{\Delta u}} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{l_{{\rm{min}}}} = \left| {{{\rm{O}}_1}{{\rm{O}}_2} - {\rm{\Delta }}{{\rm{u}}_{{\rm{max}}}}} \right|}\\{{l_{{\rm{max}}}} = \left| {{{\rm{O}}_1}{{\rm{O}}_2} + {\rm{\Delta }}{{\rm{u}}_{{\rm{max}}}}} \right|}\end{array}} \right.\)
Giả sử sóng truyền qua P rồi mới đến Q thì dao động tại P sớm pha hơn Q là:
\({\rm{\Delta }}\varphi = \frac{{2\pi \left( {PQ} \right)}}{\lambda } = \frac{{4\pi }}{3}\)
Chọn mốc thời gian để phương trình dao của phần tử tại P là: \({{\rm{u}}_1} = 5\sqrt 3 {\rm{cos}}\omega {\rm{t}}\left( {{\rm{cm}}} \right)\)
thì phương trình dao động của phần tử tại Q là: \({u_2} = 5\sqrt 3 {\rm{cos}}\left( {\omega t - \frac{{4\pi }}{3}} \right)\left( {{\rm{cm}}} \right)\).
\({\rm{\Delta }}u = {u_1} - {u_2} = 5\sqrt 3 {\rm{cos}}\left( {\omega t - \frac{{4\pi }}{3}} \right) - 5\sqrt 3 {\rm{cos}}\omega t = 15{\rm{cos}}\left( {\omega t - \frac{{5\pi }}{6}} \right)\left( {{\rm{cm}}} \right)\)
\( \Rightarrow {\rm{\Delta }}{{\rm{u}}_{{\rm{max}}}} = 15{\rm{\;cm}}\).
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{l_{{\rm{min}}}} = \left| {{O_1}{O_2} - {\rm{\Delta }}{u_{{\rm{max}}}}} \right| = \left| {10 - 15} \right| = 5{\rm{\;cm}}}\\{{l_{{\rm{max}}}} = \left| {{O_1}{O_2} + {\rm{\Delta }}{u_{{\rm{max}}}}} \right| = 10 + 15 = 25{\rm{\;cm}}}\end{array}} \right.\)
Có thể bạn quan tâm
- Trắc nghiệm Vật lí 11 KNTT Bài 9: Sóng ngang. Sóng dọc. Sự truyền năng lượng của sóng cơ (287 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Vật lí 11 KNTT Bài 8: Mô tả sóng (333 lượt thi)
- Trắc nghiệm Vật lí 11 KNTT Bài 11: Sóng điện từ (313 lượt thi)
- Trắc nghiệm Vật lí 11 KNTT Bài 14: Bài tập về sóng (231 lượt thi)
- Trắc nghiệm Vật lí 11 KNTT Bài 13: Sóng dừng (208 lượt thi)
- Trắc nghiệm Vật lí 11 KNTT Bài 12: Giao thoa sóng (207 lượt thi)
