Giải SBT Toán học 11 CTST Bài 3: Hai mặt phẳng vuông góc
Giải SBT Toán học 11 CTST Bài 3: Hai mặt phẳng vuông góc
-
50 lượt thi
-
7 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
19/07/2024Cho tứ diện ABCD có tam giác BCD vuông cân tại B và AB ^ (BCD). Cho biết BC = , AB = . Xác định và tính góc giữa hai mặt phẳng (ACD) và (BCD).
 Xem đáp án
Xem đáp án
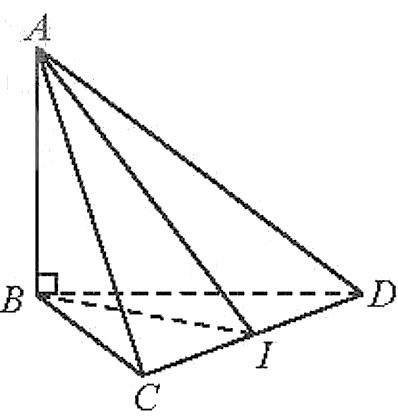
Gọi I là trung điểm của CD.
Ta có: CD ^ BI và CD ^ AB suy ra CD ^ AI.
Ta nhận thấy: CD là giao tuyến của 2 mặt phẳng (ACD) và (BCD);
Mà
Suy ra
Tam giác BCD vuông cân tại B nên
Xét tam giác ABI vuông tại B, ta có:
Vậy góc giữa hai mặt phẳng (ACD) và (BCD) là
Câu 2:
06/07/2024Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh 2a. Cho biết SA = a và SA ^ (ABCD). Trên BC lấy điểm I sao cho tam giác SDI vuông tại S. Biết góc giữa hai mặt phẳng (SDI) và (ABCD) là 60°. Tính độ dài SI.
 Xem đáp án
Xem đáp án
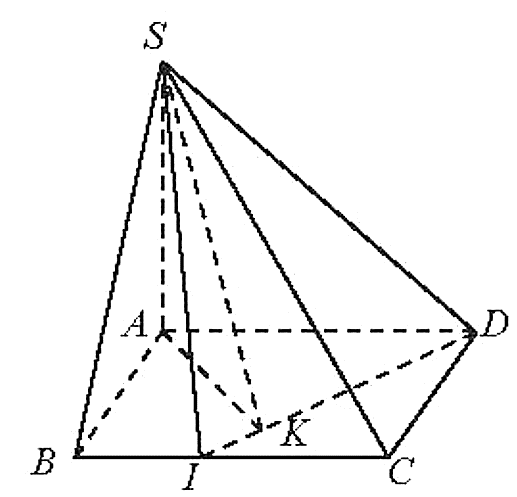
Vẽ AK ^ ID (K Î ID).
Ta có ID ^ SA và ID ^ AK (1)
Þ ID ^ (SAK) Þ ID ^ SK. (2)
Từ (1) và (2) suy ra
Xét tam giác SAK vuông tại A có:
Tam giác SAD vuông tại A, ta có:
Xét tam giác SID vuông tại S, ta có:
Do đó
Câu 3:
20/07/2024Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B và SA ^ (ABC).
a) Chứng minh rằng (SBC) ^ (SAB).
b) Gọi M là trung điểm của AC. Chứng minh rằng (SBM) ^ (SAC).
 Xem đáp án
Xem đáp án
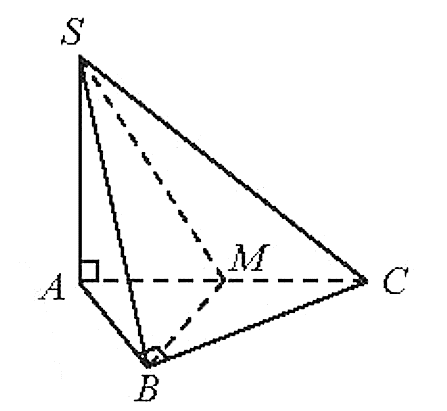
a) Ta có: BC ^ AB (giả thiết);
Đồng thời BC ^ SA (vì SA ^ (ABC)).
Þ BC ^ (SAB)
Þ (SBC) ^ (SAB).
b) Vì tam giác ABC là tam giác vuông cân tại B nên BM ^ AC.
Mà BM ^ SA (vì SA ^ (ABC))
Þ BM ^ (SAC) (1)
BM Ì (SBM) (2)
Từ (1) và (2) suy ra (SBM) ^ (SAC).
Câu 4:
19/07/2024Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt phẳng (ABCD). Gọi H và K lần lượt là hình chiếu của A trên SB và SD. Chứng minh rằng:
a) (SBC) ^ (SAB);
b) (SCD) ^ (SAD);
c) (SBD) ^ (SAC);
d) (SAC) ^ (AHK).
 Xem đáp án
Xem đáp án
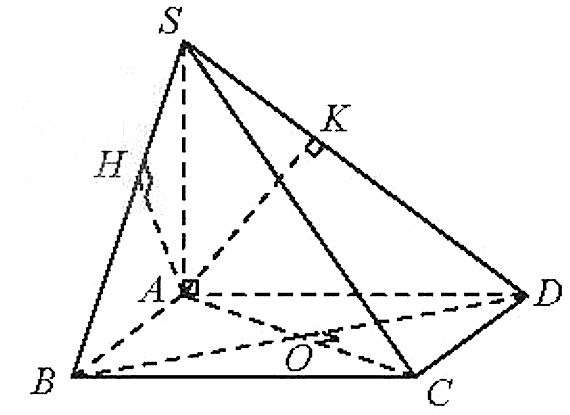
a) Theo giả thiết:
Suy ra SA ^ (ABCD).
Khi đó:
Þ BC ^ (SAB) Þ (SBC) ^ (SAB).
b) Theo giả thiết:
Suy ra SA ^ (ABCD).
Khi đó:
Þ CD ^ (SAD) Þ (SCD) ^ (SAD).
c) Ta có:
Þ BD ^ (SAC) Þ (SBD) ^ (SAC).
d) Ta có:
(SAB) ^ (SBC) (Chứng minh trên);
(SAB) Ç (SBC) = SB;
Do đó AH ^ (SBC)
Mà AH ^ SB (giả thiết).
Nên AH ^ SC. (1)
Tương tự: AK ^ SC. (2)
Từ (1) và (2) suy ra: SC ^ (AHK).
Vậy (SAC) ^ (AHK).
Câu 5:
06/07/2024Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA = . Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt đáy. Gọi (a) là mặt phẳng qua AB và vuông góc với mặt phẳng (SCD).
a) Tìm các giao tuyến của mặt phẳng (a) với các mặt của hình chóp.
b) Các giao tuyến ở câu a tạo thành hình gì? Tính diện tích của hình đó.
 Xem đáp án
Xem đáp án
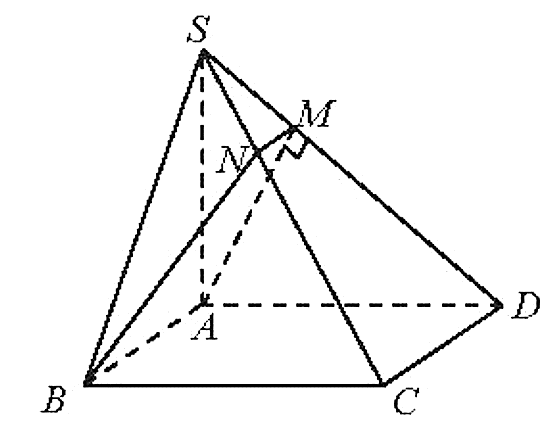
a) Ta có:
(SAB) ^ (ABCD);
(SAD) ^ (ABCD);
Do đó SA ^ (ABCD).
(SAB) Ç (SAD) = SA.
Dễ dàng chứng minh được (SAD) ^ (SCD).
Vẽ AM ^ SD (M Î SD) Þ AM ^ (SCD)
Do đó (ABM) ^ (SCD) hay (ABM) là mặt phẳng (α) qua AB và vuông góc với mặt phẳng (SCD).
Trong mặt phẳng (SCD) kẻ MN // CD (N Î SC).
Suy ra: MN // AB Þ MN Ì (α).
Vậy các giao tuyến của (α) với các mặt của hình chóp là AB, BN, NM, MA.
b)
Ta có: MN // AB; AB ^ AM (vì AB ^ (SAD)).
Suy ra ABNM là hình thang vuông tại A và M.
Tam giác SAD vuông tại A có AM là đường cao nên:
Vì MN // CD nên
Câu 6:
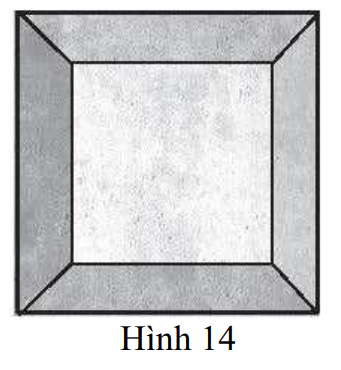
18/07/2024Người ta cần sơn tất cả các mặt của một khối bê tông hình chóp cụt tứ giác đều, đáy lớn có cạnh bằng 2 m, đáy nhỏ có cạnh bằng 1 m và cạnh bên bằng 2 m (Hình 14). Tính tổng diện tích các bề mặt cần sơn.
 Xem đáp án
Xem đáp án
Diện tích đáy lớn: S1 = 2.2 = 4 m2.
Diện tích đáy nhỏ: S2 = 1.1 = 1m2.
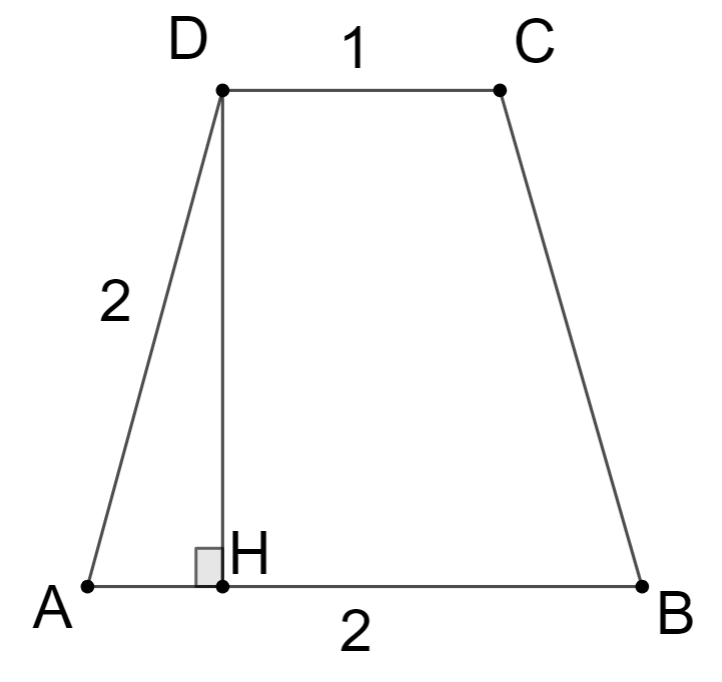
Giả sử các mặt bên có dạng như hình vẽ:
Dễ thấy: AH = 0.5 m Þ
Diện tích các mặt bên: S3 =
Tổng diện tích các mặt cần sơn là:
S = S1 + S2 + 4.S3 = 4 + 1 + 4. » 16,62 (m2).
Vậy tổng diện tích các bề mặt cần sơn khoảng 16,62 m2.
Câu 7:
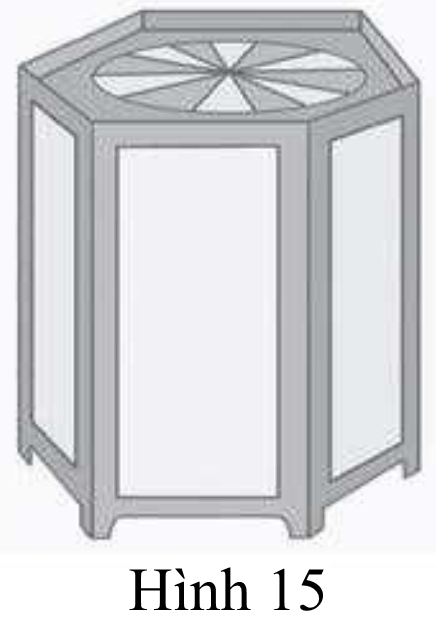
21/07/2024Một hộp đèn treo trần có hình dạng lăng trụ đứng lục giác đều (Hình 15), cạnh đáy bằng 10 cm và cạnh bên bằng 50 cm. Tính tỉ số giữa diện tích xung quanh và diện tích một mặt đáy của hộp đèn.
 Xem đáp án
Xem đáp án
Diện tích xung quanh: Sxq = 6.10.50 = 3000 (cm2).
Diện tích đáy: Sđáy = 6.(102). = 150 (cm2).
Tỉ số diện tích: .
Vậy tỉ số giữa diện tích xung quanh và diện tích một mặt đáy của hộp đèn là .
