Giải các phương trình lượng giác sau:

Giải các phương trình lượng giác sau:

a) cos(2x + 10°) = sin(50° ‒ x);

b) 8sin³x + 1 = 0;

c) (sinx + 3)(cotx ‒ 1) = 0;

d) tan(x ‒ 30°) ‒ cot50° = 0.

Giải các phương trình lượng giác sau:

Tìm tập xác định của hàm số lượng giác $y=\frac{\mathrm{s}\text{inx}-2\cos 3x}{\mathrm{s}\text{inx}+\sin \left(2x-\frac{\pi }{3}\right)}.$

Tìm các nghiệm của mỗi phương trình sau trong khoảng (‒π; π)

Tìm hoành độ các giao điểm của đồ thị các hàm số sau:

Tìm hoành độ các giao điểm của đồ thị hàm số $y=\sin 3x-\cos \left(\frac{3\pi }{4}-x\right)$ với trục hoành.

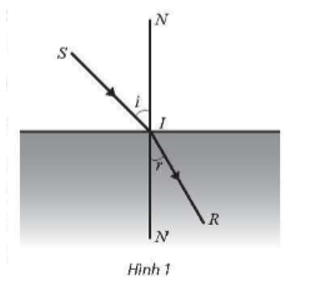
Theo định luật khúc xạ ánh sáng, khi một tia sáng được chiếu tới mặt phân cách giữa hai môi trường trong suốt không đồng chất thì tỉ số $\frac{\sin i}{\mathrm{s}\text{inr}},$ với i là góc tới và r là góc khúc xạ, là một hằng số phụ thuộc vào chiết suất của hai môi trường. Biết rằng khi góc tới là 45° thì góc khúc xạ là bao nhiêu? Làm tròn kết quả đến hàng phần trăm.

Một quả bóng được ném xiên một góc α (0° ≤ α ≤ 90°) từ mặt đất với tốc độ v₀ (m/s). Khoảng cách theo phương ngang từ vị trí ban đầu của quả bóng đến vị trí bóng chạm đất được tính bởi công thức $d=\frac{v_0^2\sin 2\alpha }{10}.$

a) Tính khoảng cách d khi bóng được ném đi với tốc độ ban đầu 10m/s và góc ném là 30° so với phương ngang.

b) Nếu tốc độ ban đầu của bóng là 10m/s thì cần ném bóng với góc bao nhiêu độ để khoảng cách d là 5 m?

Chiều cao h(m) của một cabin trên vòng quay vào thời điểm t giây sau khi bắt đầu chuyển động được cho bởi công thức $h\left(t\right)=30+20\sin \left(\frac{\pi }{25}t+\frac{\pi }{3}\right).$

a) Cabin đạt độ cao tối đa là bao nhiêu?

b) Sau bao nhiêu giây thì cabin đạt độ cao 40 m lần đầu tiên?