Giải SBT Toán 11 Cánh diều Bài tập cuối chương V
Giải SBT Toán 11 Cánh diều Bài tập cuối chương V
-
58 lượt thi
-
12 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
22/07/2024Nếu A và B là hai biến cố thì P(A ∪ B) bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Nếu A và B là hai biến cố thì P(A ∪ B) = P(A) + P(B) – P(A ∩ B).
Câu 2:
20/07/2024Nếu A và B là hai biến cố xung khắc thì P(A ∪ B) bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Nếu A và B là hai biến cố xung khắc thì P(A ∪ B) = P(A) + P(B).
Câu 3:
13/07/2024Nếu A và B là hai biến cố độc lập thì P(A ∩ B) bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Nếu A và B là hai biến cố độc lập thì P(A ∩ B) = P(A) . P(B).
Câu 4:
22/07/2024Một hộp có 10 viên bi màu hồng và 14 viên bi màu vàng, các viên bi có kích thước và khối lượng như nhau. Lấy ngẫu nhiên hai viên bi. Xét các biến cố:
P: “Hai viên bi được lấy ra có màu hồng”;
Q: “Hai viên bi được lấy ra có màu vàng”.
Khi đó, biến cố hợp của hai biến cố P và Q là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Biến cố “Hai viên bi được lấy ra có cùng màu” là biến cố hợp của hai biến cố P và Q.
Câu 5:
20/07/2024Trên giá sách có các quyển vở không nhãn xếp cạnh nhau với bề ngoài, khối lượng và kích thước giống hệt nhau, trong đó có 5 quyển ghi môn Toán, 5 quyển ghi môn Ngữ Văn và 3 quyển ghi môn Tiếng Anh. Lấy ngẫu nhiên hai quyển vở. Xét các biến cố:
M: “Trong hai quyển vở được lấy, chỉ có 1 quyển ghi môn Tiếng Anh”;
N: “Trong hai quyển vở được lấy, chỉ có 1 quyển ghi môn Ngữ Văn”.
Khi đó, biến cố giao của hai biến cố M và N là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Biến cố “Trong hai quyển vở được lấy, một quyển ghi môn Tiếng Anh và một quyển ghi môn Ngữ Văn” là biến cố giao của biến cố M và biến cố N.
Câu 6:
17/07/2024Cho n là số nguyên dương lớn hơn 2. Chọn ngẫu nhiên hai số nguyên dương từ tập hợp {1; 2; 3; …; 2n; 2n + 1}. Tính xác suất để hai số được chọn có tích là số chẵn.
 Xem đáp án
Xem đáp án
Tập {1; 2; 3; …; 2n; 2n + 1} có 2n + 1 số nguyên dương, trong đó có n + 1 số nguyên dương lẻ và n số nguyên dương chẵn.
Mỗi cách chọn ngẫu nhiên hai số nguyên dương từ 2n + 1 số nguyên dương cho ta một tổ hợp chập 2 của 2n + 1 phần tử. Do đó, không gian mẫu Ω gồm các các tổ hợp chập 2 của 2n + 1 phần tử và
Xét biến cố A :“ Hai số được chọn có tích là số chẵn”.
Có hai trường hợp xảy ra biến cố A:
⦁ Trường hợp 1: Hai số được chọn đều là số chẵn có (cách chọn).
⦁ Trường hợp 2: Hai số được chọn có một số lẻ và một số chẵn, có (cách chọn).
Suy ra, số kết quả thuận lợi cho biến cố A là
Xác suất để hai số được chọn có tích là số chẵn là:
Câu 7:
16/07/2024Người ta ghi lại tốc độ của 40 xe đạp đi qua một vị trí trên đường. Mẫu số liệu dưới đây ghi lại tốc độ của 40 xe đó (đơn vị: km/h):

a) Lập bảng tần số ghép nhóm bao gồm cả tần số tích lũy có năm nhóm ứng với năm nửa khoảng: [10 ; 12), [12 ; 14), (14 ; 16), [16 ; 18), [18 ; 20).
 Xem đáp án
Xem đáp án
Bảng tần số ghép nhóm bao gồm giá trị đại diện và tần số tích lũy của mẫu số liệu được cho như sau:
|
Nhóm |
Giá trị đại diện |
Tần số |
Tần số tích lũy |
|
[10 ; 12) |
11 |
8 |
8 |
|
[12 ; 14) |
13 |
12 |
20 |
|
[14 ; 16) |
15 |
9 |
29 |
|
[16 ; 18) |
17 |
7 |
36 |
|
[18 ; 20) |
19 |
4 |
40 |
|
|
|
n = 40 |
|
⦁ Số trung bình cộng là:
Câu 8:
17/07/2024b) Xác định các số đặc trưng đo xu thế trung tâm cho mẫu số liệu ghép nhóm trên (làm tròn các kết quả đến hàng phần mười).
 Xem đáp án
Xem đáp án
⦁ Số trung bình cộng là:
⦁ Ta có:
Vì 8 < 20 ≤ 20 nên nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 20.
Xét nhóm 2 là nhóm [12 ; 14) có r = 12, d = 2, n2 = 12 và nhóm 1 là nhóm [10 ; 12) có cf1 = 8. Suy ra trung vị là:
Tứ phân vị thứ 2 là: Q2 = Me = 14.
⦁ Vì 8 < 10 < 20 nên nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 10.
Xét nhóm 2 là nhóm [12; 14) có s = 12, h = 2, n2 = 12 và nhóm 1 là nhóm [10 ; 12) có cf1 = 8. Suy ra tứ phân vị thứ nhất là:
⦁ Vì 29 < 30 < 36 nên nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 30.
Xét nhóm 4 là nhóm [16 ; 18) có t = 16, l = 2, n4 = 7 và nhóm 3 là nhóm [14 ; 16) có cf3 = 29. Suy ra tứ phân vị thứ ba là:
⦁ Ta thấy nhóm 2 ứng với nửa khoảng [12 ; 14) là nhóm có tần số lớn nhất với u = 12, g = 2, n2 = 12; nhóm 1 là nhóm [10; 12) có n1 = 8 và nhóm 3 là nhóm [14 ; 16) có n3 = 9. Suy ra mốt là:
Câu 9:
14/07/2024Bạn Nam có 10 quyển sách sinh học, 20 quyển sách khoa học và 5 quyển sách văn học muốn mang đi quyên góp cho các thư viện gần nhà. Bạn Nam chọn ngẫu nhiên 3 quyển sách để mang tới thư viện trường. Tính xác suất ba quyển sách được chọn đôi một thể loại khác nhau.
 Xem đáp án
Xem đáp án
Mỗi cách chọn ngẫu nhiên 3 quyển sách từ 10 + 20 + 5 = 35 quyển sách cho ta một tổ hợp chập 3 của 35 phần tử. Do đó, không gian mẫu Ω gồm các tổ hợp chập 3 của 35 phần tử và
Xét biến cố A: “Ba quyển sách được chọn đôi một thể loại khác nhau”.
Ba quyển sách được chọn đôi một thể loại khác nhau tức là trong 3 quyển sách đó có 1 quyển sách sinh học, 1 quyển sách khoa học và 1 quyển sách văn học.
Chọn 1 quyển sách sinh học từ 10 quyển có 10 cách, chọn 1 quyển sách khoa học từ 20 quyển có 20 cách, chọn 1 quyển sách văn học từ 5 quyển có 5 cách.
Suy ra: n(A) = 10.20.5 = 1 000.
Vậy xác suất để ba quyển sách được chọn đôi một thể loại khác nhau là:
Câu 10:
17/07/2024Một câu lạc bộ cờ của trường có 10 bạn, trong đó có 4 bạn biết chơi cờ tướng, 6 bạn biết chơi cờ vua, mỗi bạn chỉ biết chơi một loại cờ. Nhà trường chọn ngẫu nhiên 4 bạn để tham gia buổi giao lưu cờ giữa các học sinh trong thành phố. Tính xác suất của biến cố “Trong 4 bạn được chọn, có ít nhất một bạn biết chơi cờ tướng, ít nhất một bạn biết chơi cờ vua”.
 Xem đáp án
Xem đáp án
Mỗi cách chọn ngẫu nhiên 4 bạn từ 10 bạn học sinh cho ta một tổ hợp chập 4 của 10 phần tử.
Do đó, không gian mẫu Ω gồm các tổ hợp chập 4 của 10 phần tử và
Xét biến cố A: “Trong 4 bạn được chọn, có ít nhất một bạn biết chơi cờ tướng, ít nhất một bạn biết chơi cờ vua”.
Khi đó biến cố đối của A là :“Bốn bạn được chọn chỉ chơi cờ tướng hoặc chỉ chơi cờ vua”.
Có 2 trường hợp có thể xảy ra của biến cố
⦁ Trường hợp 1: Cả bốn bạn chỉ chơi cờ tướng. Suy ra số cách chọn là
⦁ Trường hợp 2: Cả bốn bạn chỉ chơi cờ vua. Suy ra số cách chọn là
Suy ra:
Xác suất của biến cố là:
Suy ra xác suất của biến cố A là:
Câu 11:
15/07/2024Hai bạn An và Bình cùng tập ném bóng rổ một cách độc lập ở hai nửa sân khác nhau. Xác suất bạn An và bạn Bình ném bóng vào rổ lần lượt là 0,6 và 0,9. Trong cùng một lần ném, tính xác suất có ít nhất một bạn ném bóng vào rổ.
 Xem đáp án
Xem đáp án
Xét các biến cố:
A: “Bạn An ném bóng vào rổ”;
B: “Bạn Bình ném bóng vào rổ;
C: “Có ít nhất một bạn ném bóng vào rổ”.
Từ giả thiết, ta có: A, B là hai biến cố độc lập và P(A) = 0,6; P(B) = 0,9.
Suy ra: P(A ∩ B) = P(A) . P(B) = 0,6 . 0,9 = 0,54.
Ta thấy: C = A ∪ B nên xác suất có ít nhất một bạn ném bóng vào rổ là:
P(C) = P(A ∪ B) = P(A) + P(B) – P(A ∩ B) = 0,6 + 0,9 – 0,54 = 0,96.
Chú ý: Đối với bài toán này, ta có thể tính xác suất của biến cố C thông qua biến cố đối của biến cố C là: “Không có bạn nào ném bóng vào rổ”.
Câu 12:
18/07/2024Bạn Nam tham gia một trò chơi rút thăm trúng thưởng. Hộp đựng thăm có 50 lá thăm cứng với kích thước và khối lượng như nhau, trong đó có 20 lá trúng thưởng, 30 lá không trúng thưởng. Mỗi người được rút 2 lần (sau mỗi lần rút thì ghi kết quả và bỏ lại thăm vào hộp), mỗi lần 2 lá thăm. Nếu rút được 2 lá trúng thưởng thì được 1 tai nghe, nếu rút được 3 lá trúng thưởng thì được 1 tai nghe và 1 bàn phím, nếu rút được 4 lá trúng thưởng thì được 1 máy tính bảng. Tính xác suất để bạn Nam được trúng thưởng có tai nghe (làm tròn kết quả đến hàng phần mười).
 Xem đáp án
Xem đáp án
Mỗi cách chọn ngẫu nhiên 2 lá thăm từ 50 lá thăm cho ta một tổ hợp chập 2 của 50 phần tử và sau mỗi lần rút thì ghi kết quả và bỏ lại thăm vào hộp. Do đó, sau hai lần bốc thăm, số phần tử của không gian mẫu Ω là:
Xét biến cố A: “Bạn Nam được trúng thưởng có tai nghe”.
Khi đó biến cố đối của A là :“ Bạn Nam không được trúng thưởng có tai nghe”.
Có 3 trường hợp có thể xảy ra của biến cố :
+ Trường hợp 1: Trong 4 lá thăm bạn Nam rút, có 4 lá trúng thưởng. Suy ra số cách chọn:
+ Trường hợp 2: Trong 4 lá thăm bạn Nam rút, có 1 lá trúng thưởng. Suy ra số cách chọn:
+ Trường hợp 3: Trong 4 lá thăm bạn Nam rút, không có lá trúng thưởng. Suy ra số cách chọn:
Suy ra:
Xác suất của biến cố là:
Vậy xác suất để bạn Nam được trúng thưởng có tai nghe là:
Chú ý: Đối với bài toán này, chúng ta có thể tính trực tiếp xác suất của biến cố A như sau:
Sơ đồ hình cây biểu thị các khả năng thuận lợi cho biến cố A:
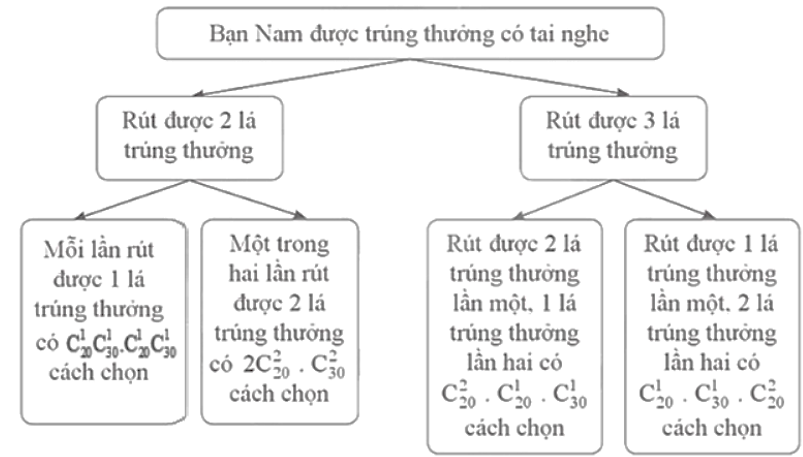
Số kết quả thuận lợi cho biến cố A là:
Vậy xác suất để bạn Nam được trúng thưởng có tai nghe là:
