Bài tập Bài tập cuối chương 9 có đáp án
Bài tập Bài tập cuối chương 9 có đáp án
-
126 lượt thi
-
7 câu hỏi
-
40 phút
Danh sách câu hỏi
Câu 1:
20/07/2024Cho tam giác ABC có là một góc tù. Lấy điểm D nằm giữa A và B; lấy điểm E nằm giữa A và C (H.9.51). Chứng minh DE < BC.
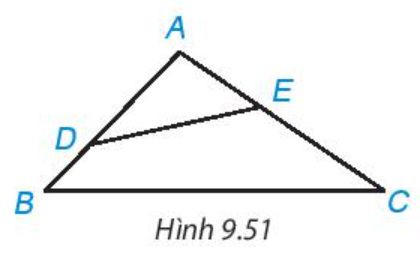
 Xem đáp án
Xem đáp án
Xét tam giác ADE có là góc ngoài của đỉnh D nên
Mà là góc tù nên là góc tù.
Xét tam giác BDE có:
là góc tù nên là góc lớn nhất trong tam giác. Do đó, BE > DE (1)
Xét tam giác ABE có là góc ngoài của đỉnh E nên
Mà là góc tù nên là góc tù.
Xét tam giác BEC có:
là góc tù nên là góc lớn nhất trong tam giác. Do đó, BC > BE (2)
Từ (1) và (2) suy ra, BC > DE (điều phải chứng minh).
Câu 2:
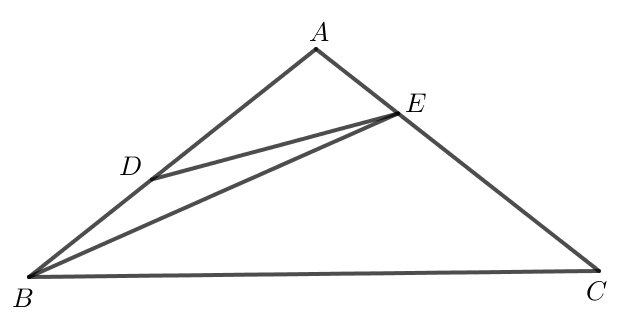
16/07/2024Cho tam giác ABC (AB > AC). Trên đường thẳng chứa cạnh BC, lấy điểm D và điểm E sao cho B nằm giữa D và C, C nằm giữa B và E, BD = BA, CE = CA (H.9.52).
a) So sánh và .
 Xem đáp án
Xem đáp án
a) Xét tam giác ABC có: AB > AC nên
Xét tam giác ABD có AB = BD nên tam giác ABD cân tại B.
Suy ra, (tính chất tam giác cân)
Ta có, là góc ngoài đỉnh B của tam giác ABD nên
Xét tam giác ACE có AC = CE nên tam giác ACE cân tại C.
Suy ra, (tính chất tam giác cân)
Ta có, là góc ngoài đỉnh C của tam giác ACE nên
Mà nên hay
Do đó,
Câu 4:
22/07/2024Gọi AI và AM lần lượt là đường cao và đường trung tuyến xuất phát từ đỉnh A của tam giác ABC. Chứng minh rằng:
a) AI < (AB + AC);
 Xem đáp án
Xem đáp án
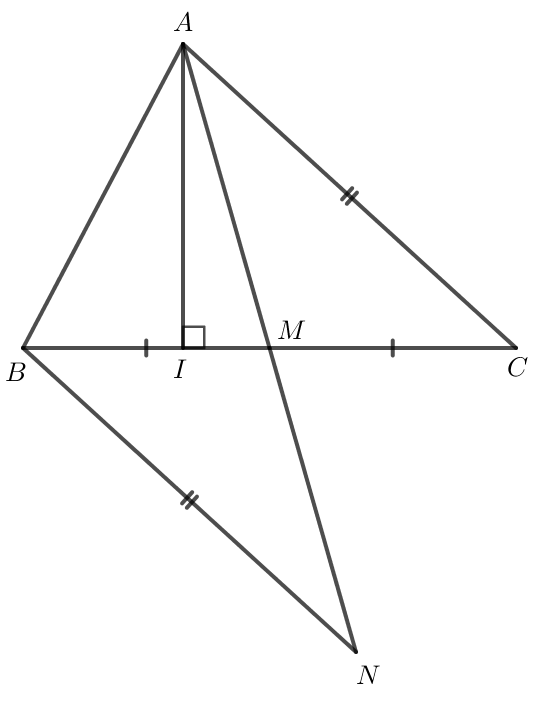
a)
vuông tại I nên AC là cạnh huyền.
Do đó AC > AI (1).
vuông tại I nên AB là cạnh huyền.
Do đó AB > AI (2).
Từ (1) và (2) ta có AB + AC > AI + Ai hay AB + AC > 2AI
Suy ra AI <
Câu 5:
16/07/2024b) AM < (AB + AC).
 Xem đáp án
Xem đáp án
b) Lấy D sao cho M là trung điểm của AD.
Xét DABM và DDCM có:
MA = MD (theo cách vẽ),
(hai góc đối đỉnh),
MB = MC (do M là trung điểm của BC),
Do đó DABM = DDCM (c.g.c)
Suy ra AB = DC (hai cạnh tương ứng).
Khi đó AB + AC = DC + AC.
Trong DACD có DC + AC > AD (bất đẳng thức tam giác)
Hay AB + AC > AD.
Mà AD = 2AM (do M là trung điểm của AD).
Suy ra AB + AC > 2AM hay AM < (AB + AC).
Vậy AM < (AB + AC).
Câu 6:
16/07/2024Cho tam giác ABC có đường phân giác AD, D nằm trên BC sao cho BD = 2DC. Trên đường thẳng AC, lấy điểm E sao cho C là trung điểm của AE (H.9.53). Chứng minh rằng tam giác ABE cân tại A.
Gợi ý. D là trọng tâm của tam giác ABE, tam giác này có đường phân giác AD đồng thời là đường trung tuyến.
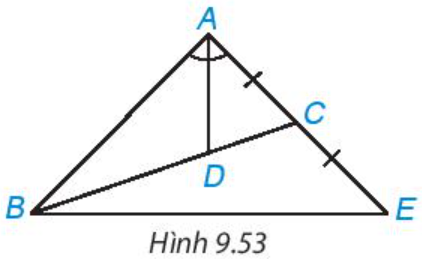
 Xem đáp án
Xem đáp án
Xét tam giác ABE có: C là trung điểm của AE nên BC là đường trung tuyến của tam giác ABE.
Ta lại có D là điểm nằm trên BC sao cho BD = 2DC.
Ta có: BC = BD + DC = 2DC + DC = 3DC.
Do đó, BC = 3DC và BC = 2BD hay .
Điểm D thuộc trung tuyến BC thỏa mãn nên D là trọng tâm tam giác ABE.
Suy ra AD là đường trung tuyến của tam giác ABE.
Xét tam giác ABE có:
AD vừa là đường trung tuyến, vừa là đường phân giác nên theo Ví dụ 1 phần Luyện tập chung, trang 82, DABE cân tại A.
Câu 7:
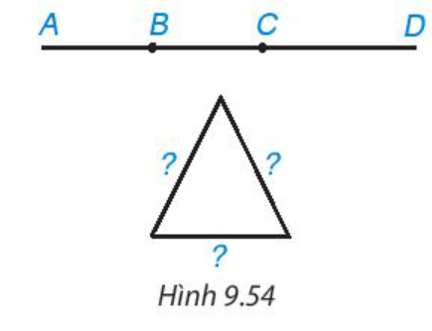
23/07/2024Một sợi dây thép dài 1,2 m. Cần đánh dấu trên sợi dây thép đó hai điểm để khi uốn gập nó lại tại hai điểm đó sẽ tạo thành tam giác cân có một cạnh dài 30 cm (H.9.54). Em hãy mô tả các cách đánh dấu hai điểm trên sợi dây thép.
 Xem đáp án
Xem đáp án
Đổi 1,2 m = 120 cm.
Chúng ta có các trường hợp sau:
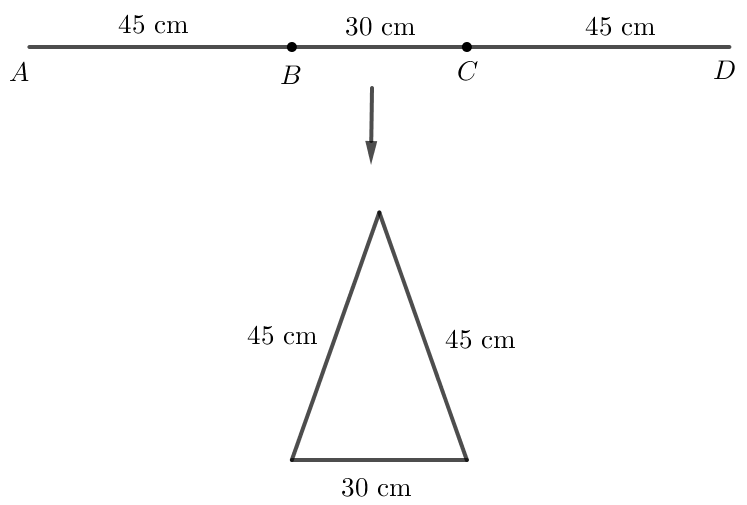
Trường hợp 1. Cạnh dài 30 cm là cạnh đáy của tam giác cân.
Khi đó độ dài 2 cạnh bên là: (120 - 30) : 2 = 45 cm.
Vậy để gấp được tam giác có ba cạnh dài 30 cm, 45 cm, 45 cm, ta đánh dấu hai điểm ở giữa hai đầu mút đoạn dây, chia đoạn dây thành ba đoạn thẳng có độ dài 30 cm, 45 cm, 45 cm, trong đó đoạn dài 30 cm chứa một mút hoặc không chứa mút nào của đoạn dây như hình vẽ dưới đây.
Trường hợp 2. Cạnh dài 30 cm là cạnh bên của tam giác cân.
Khi đó độ dài cạnh đáy là: 120 - 30 - 30 = 60 cm.
Ta thấy 30 + 30 = 60 nên bộ ba đoạn thẳng có độ dài 30 cm, 30 cm, 60 cm không thể tạo thành một tam giác.
