Câu hỏi:
17/07/2024 274Cho tam giác ABC, hai trung tuyến BM, CN cắt nhau tại G. Gọi E, F lầ lượt là trung điểm của GB và GC.
a) Chứng minh tứ giác MNEF là hình bình hành
b) Lấy I, J thuộc tia đối của MG và NG sao cho MI = MG và NI = NG. Chứng minh tứ giác BCIJ là hình bình hành.
Trả lời:
Giải bởi Vietjack
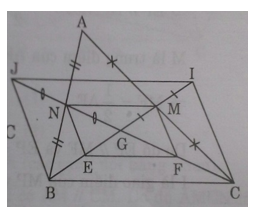
a) Ta có MN là đường trung bình của ΔABC
⇒ MN // BC và MN = BC/2
Tương tự EF là đường trung bình của ΔBGC nên EF // BC và EF = BC/2
Do đó MN // EF và MN = EF.
Vậy MNEF là hình bình hành (hai cạnh đối vừa song song vừa bằng nhau)
b) Ta có G là trong tâm của ΔABC nên GN = GC/2
Mà GN = JN (gt) ⇒ GJ = GC.
Tương tự ta có GI = GB
Vậy tứ giác BJIC là hình bình hành (hai đường chéo cắt nhau tại trung điểm mỗi đường).
