Câu hỏi:
16/07/2024 186
Cho hình chóp tam giác đều S.ABC có tất cả các cạnh bằng nhau, chiều cao mặt đáy bằng \[3\sqrt 3 \,\,{\rm{cm}}\]. Tính chiều cao mặt bên hình chóp.
A. \[3\sqrt 3 \,\,{\rm{cm}}\]
B. 3 cm
C. \[\frac{{3\sqrt 3 }}{2}\,\,{\rm{cm}}\]
D. \[\frac{3}{2}\,\,{\rm{cm}}\]
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải
Đáp án đúng là: A
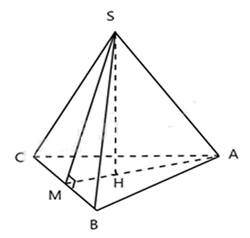
Hình chóp tam giác đều S.ABC có tất cả các cạnh bằng nhau nên
SA = SB = SC = AB = AC = BC.
Gọi H là trọng tâm tam giác ABC đều, M là trung điểm BC.
Theo định nghĩa trung đoạn, SM là trung đoạn của hình chóp.
Đáy ABC là tam giác đều nên AM vừa là trung tuyến vừa là đường cao
Suy ra \[{\rm{AM}} \bot {\rm{BC}} \Rightarrow \widehat {{\rm{AMB}}}{\rm{ = 90}}^\circ \Rightarrow {\rm{\Delta AMB}}\] vuông tại M.
\[{\rm{AM = 3}}\sqrt {\rm{3}} \,\,{\rm{cm}}\].
Ta có: SA = SB = SC nên tam giác SAB đều
Khi đó, SM vừa là trung tuyến vừa là đường cao.
\[ \Rightarrow {\rm{SM}} \bot {\rm{BC}} \Rightarrow \widehat {{\rm{SMB}}}{\rm{ = 90}}^\circ \Rightarrow {\rm{\Delta SMB}}\] vuông tại M.
Xét tam giác vuông SMB và tam giác vuông AMB có:
MB chung
SB = AB
Do đó \[{\rm{\Delta SMB = \Delta AMB}}\] (cạnh huyền – cạnh góc vuông)
Suy ra \[{\rm{SM = AM = 3}}\sqrt {\rm{3}} \,\,{\rm{(cm)}}\].
Vậy chiều cao mặt bên hình chóp SM bằng \[{\rm{3}}\sqrt {\rm{3}} \,\,{\rm{cm}}\].
Lời giải
Đáp án đúng là: A

Hình chóp tam giác đều S.ABC có tất cả các cạnh bằng nhau nên
SA = SB = SC = AB = AC = BC.
Gọi H là trọng tâm tam giác ABC đều, M là trung điểm BC.
Theo định nghĩa trung đoạn, SM là trung đoạn của hình chóp.
Đáy ABC là tam giác đều nên AM vừa là trung tuyến vừa là đường cao
Suy ra \[{\rm{AM}} \bot {\rm{BC}} \Rightarrow \widehat {{\rm{AMB}}}{\rm{ = 90}}^\circ \Rightarrow {\rm{\Delta AMB}}\] vuông tại M.
\[{\rm{AM = 3}}\sqrt {\rm{3}} \,\,{\rm{cm}}\].
Ta có: SA = SB = SC nên tam giác SAB đều
Khi đó, SM vừa là trung tuyến vừa là đường cao.
\[ \Rightarrow {\rm{SM}} \bot {\rm{BC}} \Rightarrow \widehat {{\rm{SMB}}}{\rm{ = 90}}^\circ \Rightarrow {\rm{\Delta SMB}}\] vuông tại M.
Xét tam giác vuông SMB và tam giác vuông AMB có:
MB chung
SB = AB
Do đó \[{\rm{\Delta SMB = \Delta AMB}}\] (cạnh huyền – cạnh góc vuông)
Suy ra \[{\rm{SM = AM = 3}}\sqrt {\rm{3}} \,\,{\rm{(cm)}}\].
Vậy chiều cao mặt bên hình chóp SM bằng \[{\rm{3}}\sqrt {\rm{3}} \,\,{\rm{cm}}\].
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Cho hình chóp tam giác đều S.ABC biết SA = 4 cm, AB = 3 cm. Chọn phát biểu đúng.
Câu 4:
Cho hình chóp tam giác đều S.ABC, có SA = 4cm, AB = 5cm. So sánh độ dài cạnh SB và SC.
Câu 5:
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng nhau và bằng 6 cm. Chu vi mặt đáy của hình chóp tứ giác đều S.ABCD
Câu 6:
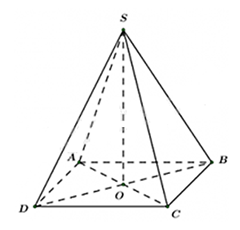
Cho hình chóp tứ giác đều S.ABCD như hình. Gọi O là giao điểm hai đường chéo, khi đó SO là:

Câu 7:
Cho hình chóp tứ giác đều có tất cả các cạnh bằng nhau, nếu tăng cạnh bên lên hai lần thì chu vi mặt đáy sẽ
Câu 12:
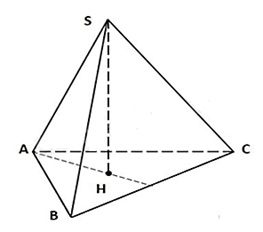
Cho hình chóp tam giác đều SABC như hình. Mặt đáy của hình chóp là

Câu 13:
Bạn A định gấp một hộp quà từ tấm bìa như hình dưới. Bạn A định gấp hình gì?