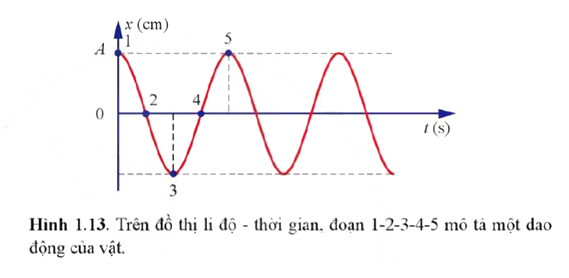
Câu hỏi:
17/07/2024 62
Với một cái thước mỏng đàn hồi, hãy đề xuất phương án tạo ra dao động tự do của thước và mô tả cách làm.
Với một cái thước mỏng đàn hồi, hãy đề xuất phương án tạo ra dao động tự do của thước và mô tả cách làm.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
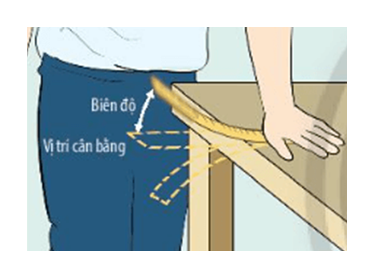
Bố trí thí nghiệm như hình trên:
- Một đầu thước đặt trên mặt bàn, dùng một tay giữ chặt đầu thước đó lại.
- Dùng tay còn lại gẩy mạnh đầu còn lại của thước.
Ta thấy đầu thước tự do dao động quay vị trí cân bằng. Gẩy càng mạnh thì thước dao động càng mạnh và ngược lại.

Bố trí thí nghiệm như hình trên:
- Một đầu thước đặt trên mặt bàn, dùng một tay giữ chặt đầu thước đó lại.
- Dùng tay còn lại gẩy mạnh đầu còn lại của thước.
Ta thấy đầu thước tự do dao động quay vị trí cân bằng. Gẩy càng mạnh thì thước dao động càng mạnh và ngược lại.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Đồ thị Hình 1.18 biểu diễn hai dao động ngược pha. Dựa vào đồ thị, xác định độ lệch pha của hai dao động này.
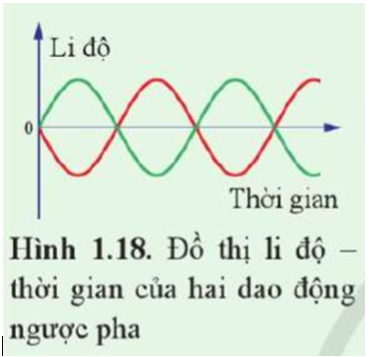
Đồ thị Hình 1.18 biểu diễn hai dao động ngược pha. Dựa vào đồ thị, xác định độ lệch pha của hai dao động này.

Câu 2:
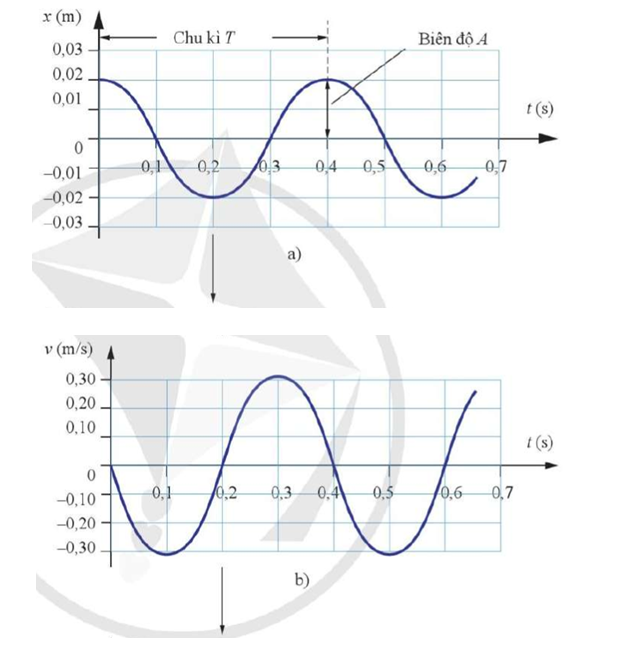
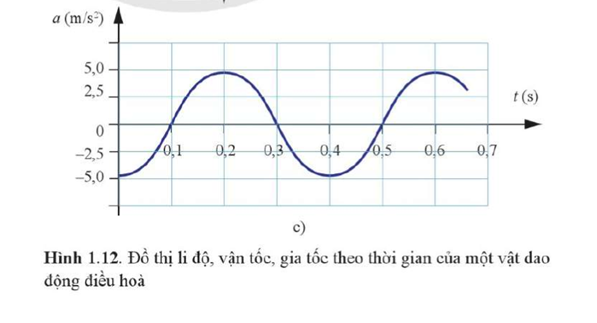
Dựa vào độ dốc của đồ thị li độ - thời gian, ta có thể xác định vận tốc của xe kĩ thuật số tại mỗi thời điểm. Từ các số liệu này, có thể vẽ được đồ thị hình sin biểu diễn sự liên hệ giữa vận tốc và thời gian (Hình 1.12b). Ví dụ, trong Hình 1.12a, tại t = 0, độ dốc của đồ thị li độ – thời gian bằng 0, vận tốc bằng 0. Khi t tăng từ 0 s đến 0,2 s, độ dốc âm, vận tốc có giá trị âm. Tại t = 0,2 s, độ dốc bằng 0 một lần nữa. Từ t = 0,2 s đến t = 0,4 s, độ dốc dương, vận tốc có giá trị dương. Độ dốc của đồ thị li độ – thời gian có độ lớn cực đại tại các thời điểm t = 0,1 s; 0,3 s; 0,5 s... Bằng cách tương tự, dựa vào độ dốc của đồ thị vận tốc – thời gian ở Hình 1.12b, ta có thể tìm được gia tốc của xe tại mỗi thời điểm và vẽ được đồ thị hình sin như Hình 1.12c.
Dựa vào các đồ thị ở Hình 1.12, tìm:
Các thời điểm gia tốc của xe bằng 0.
Các thời điểm gia tốc của xe cực đại.
Giải thích cách làm.
Dựa vào độ dốc của đồ thị li độ - thời gian, ta có thể xác định vận tốc của xe kĩ thuật số tại mỗi thời điểm. Từ các số liệu này, có thể vẽ được đồ thị hình sin biểu diễn sự liên hệ giữa vận tốc và thời gian (Hình 1.12b). Ví dụ, trong Hình 1.12a, tại t = 0, độ dốc của đồ thị li độ – thời gian bằng 0, vận tốc bằng 0. Khi t tăng từ 0 s đến 0,2 s, độ dốc âm, vận tốc có giá trị âm. Tại t = 0,2 s, độ dốc bằng 0 một lần nữa. Từ t = 0,2 s đến t = 0,4 s, độ dốc dương, vận tốc có giá trị dương. Độ dốc của đồ thị li độ – thời gian có độ lớn cực đại tại các thời điểm t = 0,1 s; 0,3 s; 0,5 s... Bằng cách tương tự, dựa vào độ dốc của đồ thị vận tốc – thời gian ở Hình 1.12b, ta có thể tìm được gia tốc của xe tại mỗi thời điểm và vẽ được đồ thị hình sin như Hình 1.12c.
Dựa vào các đồ thị ở Hình 1.12, tìm:
Các thời điểm gia tốc của xe bằng 0.
Các thời điểm gia tốc của xe cực đại.
Giải thích cách làm.
Câu 3:
Nếu bỏ qua lực cản, chuyển động nào sau đây là dao động tự do:
A. Một con muỗi đang đập cánh.
B. Tòa nhà rung chuyển trong trận động đất.
C. Mặt trống rung động sau khi gõ.
D. Bông hoa rung rinh trong gió nhẹ.
Nếu bỏ qua lực cản, chuyển động nào sau đây là dao động tự do:
A. Một con muỗi đang đập cánh.
B. Tòa nhà rung chuyển trong trận động đất.
C. Mặt trống rung động sau khi gõ.
D. Bông hoa rung rinh trong gió nhẹ.
Câu 4:
Xác định biên độ, chu kì và tần số của dao động có đồ thị li độ – thời gian được biểu diễn ở Hình 1.9.
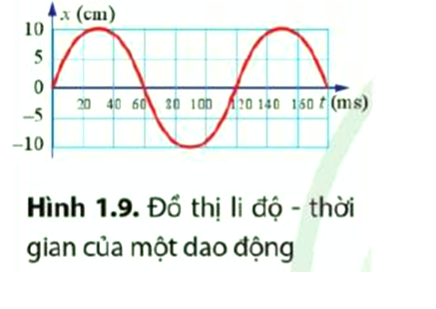
Xác định biên độ, chu kì và tần số của dao động có đồ thị li độ – thời gian được biểu diễn ở Hình 1.9.

Câu 5:
Một vật dao động điều hòa với phương trình li độ: . Xác định pha của dao động tại thời điểm s.
Một vật dao động điều hòa với phương trình li độ: . Xác định pha của dao động tại thời điểm s.
Câu 6:
Dựa vào đồ thị Hình 1.12, xác định các đại lượng sau:
a) Tần số góc của dao động.
b) Biên độ của dao động.
c) Vận tốc cực đại của vật dao động.
d) Gia tốc cực đại của vật dao động.
Câu 7:
Hằng ngày, chúng ta thấy rất nhiều chuyển động, trong đó, vật chuyển động qua lại quanh một vị trí cân bằng. Chuyển động của người chơi đu là một ví dụ như vậy (Hình 1.1).

Những chuyển động đó được gọi là dao động. Mô tả dao động như thế nào?
Hằng ngày, chúng ta thấy rất nhiều chuyển động, trong đó, vật chuyển động qua lại quanh một vị trí cân bằng. Chuyển động của người chơi đu là một ví dụ như vậy (Hình 1.1).

Những chuyển động đó được gọi là dao động. Mô tả dao động như thế nào?
Câu 9:
Tim co bóp theo nhịp do được điều khiển bằng một hệ thống các xung điện dẫn truyền trong cơ tim. Máy điện tim ghi nhận những xung điện này và hiển thị dưới dạng đường điện tâm đồ. Đó là những đường gấp khúc, lên xuống biến thiên theo nhịp co bóp của tim.
Dựa vào hình ảnh điện tâm đồ ở Hình 1.10, xác định chu kì đập của tim. Biết rằng mỗi khoảng vuông (theo chiều ngang) tương ứng với khoảng thời gian 0,12 s.
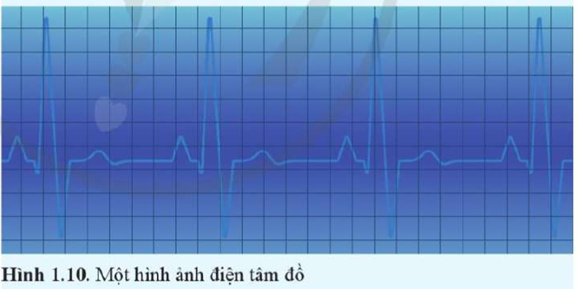
Tim co bóp theo nhịp do được điều khiển bằng một hệ thống các xung điện dẫn truyền trong cơ tim. Máy điện tim ghi nhận những xung điện này và hiển thị dưới dạng đường điện tâm đồ. Đó là những đường gấp khúc, lên xuống biến thiên theo nhịp co bóp của tim.
Dựa vào hình ảnh điện tâm đồ ở Hình 1.10, xác định chu kì đập của tim. Biết rằng mỗi khoảng vuông (theo chiều ngang) tương ứng với khoảng thời gian 0,12 s.

Câu 10:
Tần số góc và tần số của dao động điều hoà có liên hệ như thế nào?
Tần số góc và tần số của dao động điều hoà có liên hệ như thế nào?
Câu 11:
Mô tả trạng thái của hai vật dao động ở thời điểm t3 và t4, trong đồ thị Hình 1.14.
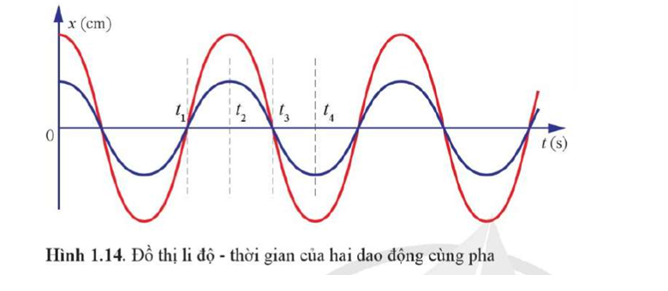
Mô tả trạng thái của hai vật dao động ở thời điểm t3 và t4, trong đồ thị Hình 1.14.

Câu 12:
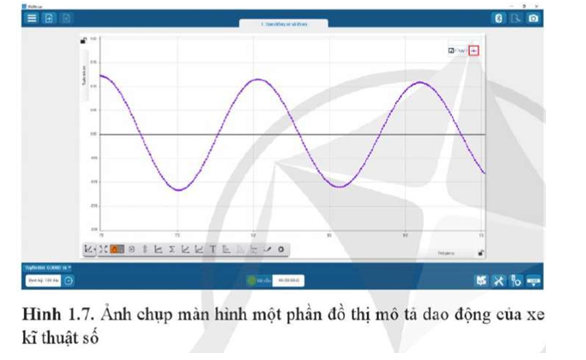
Từ đồ thị Hình 1.7, mô tả sự thay đổi li độ của xe theo thời gian.
Câu 15:
Dụng cụ
Quả cầu kim loại nhỏ, sợi dây mảnh nhẹ, giá thí nghiệm.
Tiến hành
+ Treo quả cầu vào giá thí nghiệm.
+ Khi quả cầu đứng yên tại vị trí cân bằng, dây treo có phương thẳng đứng, kéo quả cầu khỏi vị trí cân bằng một đoạn nhỏ rồi buông tay cho quả cầu chuyển động (Hình 1.2).
+ Mô tả chuyển động của quả cầu.